金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
登陆有奖并可浏览互动!
您需要 登录 才可以下载或查看,没有账号?立即注册


×
经典影子层析(classical shadow tomography)是近年来发展的一套量子测量方案[1][2][3][4][5],它力求用较少的测量次数求得尽可能多的观测量均值,从而高效地将量子信息读取为经典信息。
本文简要介绍这一方案。
<hr/>1. 测量和层析
首先回顾一下传统的量子测量和量子态层析。
若想要知道一个量子态 \rho 关于某个观测量 O 的期望值 \langle O\rangle_\rho=\operatorname{tr}(O\rho) ,通常的步骤是
- 重复地制备这个态 M 次;
- 在该观测量的本征基底 \{|\lambda\rangle\} 下进行测量;
- 对测量结果取平均 \langle O\rangle_\rho=\sum_\lambda \langle\lambda|\rho|\lambda\rangle \lambda\leftarrow\frac{1}{M}\sum_m \lambda_m 。
其中 \lambda 和 |\lambda\rangle 表示 O 的本征值和本征态,即 O=\sum_{\lambda}\lambda|\lambda\rangle\langle\lambda| 。 \lambda_m 表示第 m 次测量得到的结果。
注:根据大数定律,测量均值会收敛于严格的期望,标准差以 \frac{1}{\sqrt{M}} 的速率趋于零。 若想知道多个观测量的均值,直接的方法是对每个观测量都依次完成上述步骤。
若想知道所有观测量的均值,直接的方法是对一套完备的观测基底都依次完成上述步骤。这个过程又称为量子态(完全)层析。因为根据完备观测量的期望可以重构密度矩阵,而密度矩阵包含了量子态的所有信息。
注:这里提到的全部信息,除了观测量期望外,还包括密度矩阵的非线性函数,例如纯度/熵、负值度等。 以 N-qubit 系统为例,Hilbert 空间维数记为 d=2^{N} 。所有 Pauli string \{P\} 构成了矩阵空间的一套完备正交基(Hilbert-Schmidt 内积),共 4^n=d^2 个。密度矩阵可以展开为
\begin{aligned} \rho&=\sum_{P}\frac{\operatorname{tr}(P\rho)}{\|P\|_2} \frac{P}{\|P\|_2} = \sum_{P}\frac{\operatorname{tr}(P\rho)P}{\operatorname{tr}(P^2)}\\ &=\sum_{P}\frac{\operatorname{tr}(P\rho)P}{\operatorname{tr}I} =\frac{I+\vec{r}\cdot\vec{P}}{d}. \end{aligned}
其中 \vec{P} 表示所有非平凡(即除恒等算符外)的 Pauli string 组成的矢量, \vec{r}=\{\langle P\rangle_\rho\}_{P\neq I} 代表所有非平凡 Pauli string 在该态上的期望值所组成的一个实矢量。
由于不同表象下的模相等,故有
\begin{aligned} \operatorname{tr}(\rho^2)=\sum_\sigma \left|\frac{\operatorname{tr}(\sigma\rho)}{\|\sigma\|_2}\right|^2 = \frac{1+\vec{r}^2}{d}, \end{aligned}
注:等式左边可以理解为以 01 矩阵元 [A(i,j)]_{i'j'}=\delta_{ii'}\delta_{jj'} 为基底做展开时的矢量模方。 进而矢量 \vec{r} 满足不等式
\vec{r}^2=\operatorname{tr}(\rho^2)d-1\leq d-1.
因此,维数为 d 的量子态可以与一个半径为 \sqrt{d-1} 的 d^2-1 维球体(即 Bloch 球)中的点一一对应
\begin{aligned} \rho\rightarrow \vec{r}=\{\langle P\rangle_\rho\}_{P\neq I}\rightarrow\rho=\frac{I+\vec{r}\cdot\vec{P}}{d}. \end{aligned}
注:特别地,球表面对应的态满足 \operatorname{tr}(\rho^2)=1 ,表示所有纯态。 通过测量所有 Pauli string 得到 \vec{r} ,就得到了 \rho 的密度矩阵。
比如对于单个 qubit,有
\vec{r}=\{\langle X\rangle_\rho, \langle Y\rangle_\rho, \langle Z\rangle_\rho\}.
\begin{aligned} \rho=\frac{I+\langle X\rangle_\rho X+\langle Y\rangle_\rho Y+\langle Z\rangle_\rho Z}{2}. \end{aligned}
也就是说,单比特量子态层析只要测量 3 个 Pauli 算符 X,Y,Z 的均值。
然而对于 N 个 qubits 的情况,量子态层析需要测量所有 4^N-1 个 Pauli string 的均值,测量成本随比特数目指数增长。
注:事实上有一些 Pauli string 是对易的,例如 Z\otimes I 和 I\otimes X ,它们可以共享一个测量基底。因此,测量成本应当正比于不同的测量基底的个数,即 \#\{|x\pm\rangle,|y\pm\rangle,|z\pm\rangle\}^{\otimes N}=3^N 。 量子态层析的好处在于,当我们并不知道要测哪些量时,先测量一套完备的基底并保存结果,以后无论需要哪个量的观测期望,都可以通过重构的密度矩阵去预测。(“先测量,再提问。”)
然而我们看到,量子态层析的复杂度随系统大小指数增长,不可规模化。
注:不仅时间复杂度指数增长,为了记录下所有 Pauli string 均值所需的空间复杂度也是指数增长的。 于是一个自然的问题是,如果我们对于以后要测的量只有一些初步的认识,例如所关心观测量是局域的、少体的、低秩的等,那么是否可以改进完全层析的方案,使其可规模化呢?
答案是肯定的,经典影子层析给出了一套解决方案。
<hr/>2. 经典影子层析
2.1 启发式推导
经典影子层析的出发点是对完全层析的求和式进行抽样近似。这一点类似蒙卡,引入随机性,用抽样求平均代替完全求和。
但它又比单纯的经典抽样要更一般一些。概括地说,经典影子层析分为两步:
随机测量(randomized measurement) + 经典后处理(classical post-processing)。
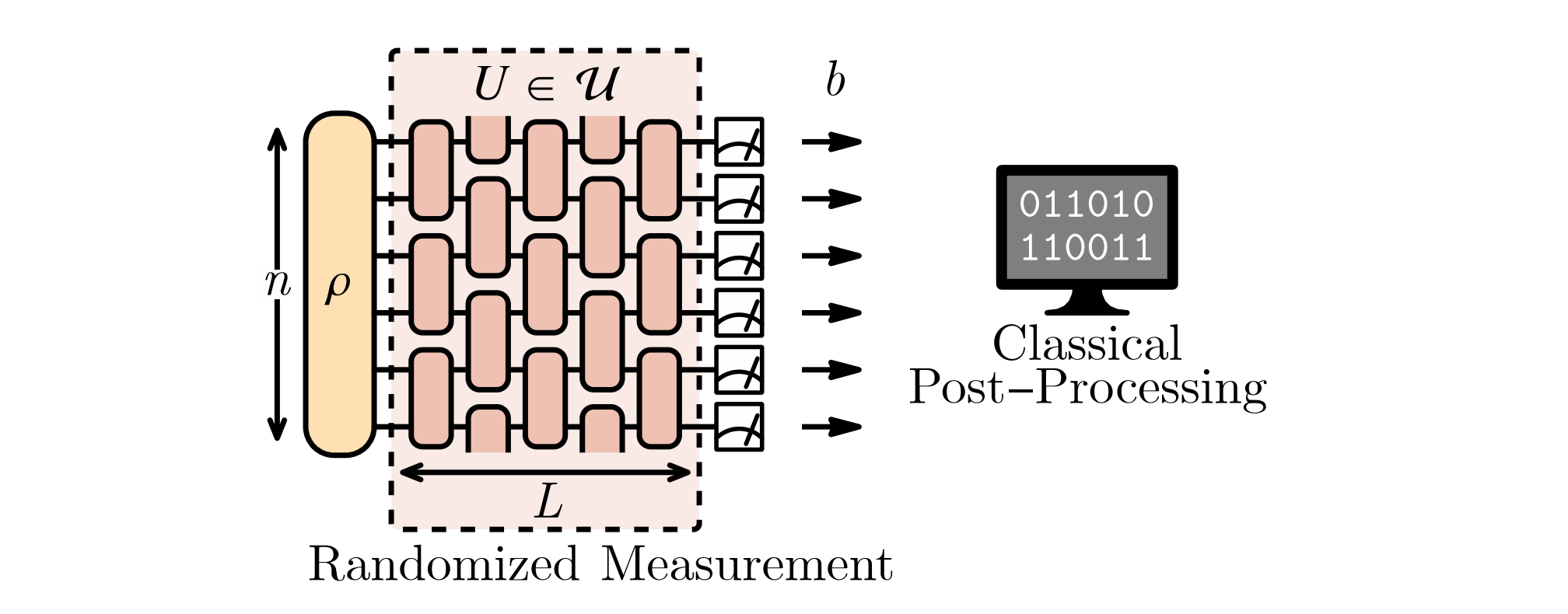
Schematic for classical shadow tomography from Ref[4].
下面我们做一个启发式的推导,来引出算法的框架。
首先,为了重构出 \rho ,必须在许多不同的测量基底上进行测量,即作用一些幺正变换把 computational basis 旋转到不同的基底上。
我们把这些幺正变换所组成的系综记为 \mathbb{U} 。
注:之所以称为系综而不是单纯的集合,是因为我们隐含地在其上定义了一个概率分布 \operatorname{Pr}_\mathbb{U}[U],一般选为均匀分布(Haar measure)。 对于每个制备好的目标测量态 \rho ,采样一个 U\in\mathbb{U} 并以量子线路的方式作用到 \rho 上,得到输出态 U\rho U^\dagger 。
然后对输出态在 computational basis 上进行测量,得到结果记为 b 。
等价地,相当于在旋转后的基底上测得了结果 \hat{\sigma}=U^\dagger|b\rangle\langle b|U 。
注:
1. 此处一个测量结果 \hat{\sigma} 称作一个 classical snapshot。
2. 作为测量结果,此处 b 的分布是依赖于 \mathbb{U} 和 \rho 的,从而 \hat{\sigma} 的分布也是依赖于 \mathbb{U} 和 \rho 的。 现在我们来考察随机测量 \rho 得到结果 \hat{\sigma} 的概率 \operatorname{Pr}_{\mathbb{U},\rho}[\hat{\sigma}] 是多少。
得到 \hat{\sigma} 需要两个条件:
- 随机选中了 U ,转到了要测得 \hat{\sigma} 所必需的测量基底上,此事件发生概率(密度)为 \operatorname{Pr}_\mathbb{U}[U] ;
- 在该基底上进行测量时, \rho 坍缩到了 \hat{\sigma} 上,此事件发生概率为 \operatorname{tr}(\hat{\sigma}\rho) (Born's rule)。
两个事件相互独立,因此随机测量 \rho 得到结果 \hat{\sigma} 的概率是两者的乘积,即
\boxed{ \operatorname{Pr}_{\mathbb{U},\rho}[\hat{\sigma}]=\operatorname{Pr}_\mathbb{U}[U]\operatorname{tr}(\hat{\sigma}\rho).}\\特别地,随机测量最大混态得到结果 \hat{\sigma} 的概率为
\begin{aligned} \operatorname{Pr}_{\mathbb{U},I/d}[\hat{\sigma}]=\operatorname{Pr}_\mathbb{U}[U]\operatorname{tr}(\hat{\sigma}\frac{I}{d})=\frac{\operatorname{Pr}_\mathbb{U}[U]}{d} . \end{aligned}
注:
1. 此时无论 U 取何值,最大混态经过幺正变换后仍是最大混态,故测量得出的 b 的分布始终是均匀分布,不再依赖于 U。这正是上式中 1/d 因子的由来。
2. 在不知道 \rho 的任何信息时,根据贝叶斯的精神应假定它处于最大混态。因此 \operatorname{Pr}_{\mathbb{U},I/d}[\hat{\sigma}] 可以看作一个先验分布, \operatorname{Pr}_{\mathbb{U},\rho}[\hat{\sigma}] 可以看作后验分布。 于是随机测量 \rho 得到结果 \sigma 的概率可以重写为
\operatorname{Pr}_{\mathbb{U},\rho}[\hat{\sigma}]=d\operatorname{Pr}_{\mathbb{U},I/d}[U]\operatorname{tr}(\hat{\sigma}\rho).
可以发现 snapshot 的期望可以写成
\begin{aligned} \sigma=\mathbb{E}_{\mathbb{U},\rho} [\hat{\sigma}] = d~\mathbb{E}_{\mathbb{U},I/d}[\hat{\sigma} \operatorname{tr}(\hat{\sigma}\rho)]. \end{aligned}
上式可以看作一个从密度矩阵到密度矩阵的线性映射,即一个量子信道
\sigma=\mathcal{M}(\rho),
其中
\mathcal{M}(\cdot)=d~\mathbb{E}_{\mathbb{U},I/d}[\hat{\sigma} \operatorname{tr}(\hat{\sigma}\cdot)],
称为这种随机测量方案的测量信道(measurement channel)。
用张量网络图示可以表示为

Tensor network diagram for the measurement channel.
注:此处密度矩阵上下指标分别结合左右矢。信道图示采用了 Liouville 超算符。 若该测量信道可逆,则有
\rho=\mathcal{M}^{-1}(\sigma).
至此,我们重构出了密度矩阵。 \mathcal{M}^{-1} 称为重构映射(reconstruction map)。
注:测量信道可逆的一个充分条件是, \mathbb{U} 生成的测量基底族是层析完备的(tomographically complete)[2]。 如果我们要通过 \sigma 拿到 \rho ,需要知道 \mathcal{M}^{-1} 的显式表达式,或者可以通过一套经典算法来求得 \mathcal{M}^{-1}。
这对于常用的系综是可以做到的。例如对于均匀分布,可以通过 Schur 引理 / Weingarten 矩阵求出
\begin{aligned} \mathcal{M}_{\text{Haar}}(\rho)=\frac{\operatorname{tr}(\rho)I+\rho}{d+1}. \end{aligned}
注:由于以上推导只涉及到概率分布的二阶矩,故只要 \mathbb{U} 是一个 unitary 2-design,上式就成立。 这可以看作 depolarizing 信道的一个特例,其逆映射为
\mathcal{M}^{-1}_{\text{Haar}}(\sigma)=(d+1)\sigma-\operatorname{tr}(\sigma)I.
注:量子信道的逆映射不一定是合法的量子信道,可能不再满足完全正定性。例如此处若 \sigma 为一个纯态,逆映射的结果会因为减去了一个 identity 而变得不再正定。当然,反过来说,若 \sigma 本身就是某个量子态 depolarizing 后的结果,则 \sigma 也不可能是个纯态(但组成 \sigma 的一个 snapshot \hat{\sigma} 可以是)。 2.2 一般框架
在上一节我们看到,通过随机测量、对结果取平均、再作用重构信道,确实可以得到 \rho 。
但我们并不需要真的重构出矩阵 \rho ,因为这需要消耗指数多的储存空间。我们只需要求出一些观测量的期望。
因此,我们首先将重构映射和求期望交换,得到
\rho=\mathcal{M}^{-1}(\sigma)=\mathbb{E}_{\mathbb{U},\rho} [\mathcal{M}^{-1}(\hat{\sigma})]=\mathbb{E}_{\mathbb{U},\rho} [\hat{\rho}].
其中 \hat{\rho}=\mathcal{M}^{-1}(\hat{\sigma}) 称为 \rho 的 classical shadow。由上式可知,作为一个随机变量, \hat{\rho} 是 \rho 的一个无偏估计(unbiased estimator)。
注:
1. 从上一小节可知, \hat{\rho} 不一定是一个合法的密度矩阵。
2. 为了在经典计算机上高效地计算 \hat{\sigma} ,量子线路 U 一般限制为 Clifford 线路,从而在多项式时间内模拟。 观测量期望可以表示为
\langle O\rangle_\rho=\operatorname{tr}(O\rho)=\mathbb{E}_{\mathbb{U},\rho}[\operatorname{tr}(O\hat{\rho})]=\mathbb{E}_{\mathbb{U},\rho}[\operatorname{tr}(O\mathcal{M}^{-1}(\hat{\sigma}))].
另外,层析完备性保证了 \mathcal{M}^{-1} 作为线性变换是厄米的,因此
\langle O\rangle_\rho=\mathbb{E}_{\mathbb{U},\rho}[\operatorname{tr}(\mathcal{M}^{-1}(O)\hat{\sigma})].
算法实现中作用于 O 还是 \hat{\sigma} 可以根据方便自行选择。
至此,我们完成了经典影子层析的全部推导。算法框架可以总结为
- 选定一个幺正变换的系综 \mathbb{U} ,计算出 \mathbb{U} 所对应的重构映射 \mathcal{M}^{-1} ;
- 根据 \mathbb{U} 随机选择一个幺正变换 U ,以量子线路的形式作用到 \rho 上;
- 对作用后的态进行测量,得到结果 b ,记此组数据 (U,b) ,返回上一步,直至收集到足够的数据;
- 每组数据 (U,b) 可以生成一个 \hat{\sigma} ,通过重构映射 \mathcal{M}^{-1} 得到 \hat{\rho} ,进而得到观测量的一个样本 \operatorname{tr}(O\hat{\rho}) ,对该样本取平均就得到了观测量均值 \langle O\rangle_\rho 。
值得注意的是,中间两步在量子设备上完成,首尾两步在经典计算机上完成。
注:除了像 Pauli string 这样的常见观测量,该算法还可以用来计算保真度、纯度/熵、投影等。因为密度矩阵得到重构后,原本在量子设备上的操作可以等效地转化为经典操作,例如计算纯度 \operatorname{tr}(\rho^2)=\mathbb{E}_{\mathbb{U},\rho}[\operatorname{tr}(\hat{\rho}\hat{\rho}')] 。 上述通过采样求均值的方案有效的前提是,样本的方差不能太大,至少不能随系统规模指数增长。否则根据大数定律,我们就需要指数多的样本来压制误差才能获得可靠的结果。
2.3 方差分析
随机测量中单个样本的方差可以放缩为
\begin{aligned} \operatorname{Var}_{\mathbb{U},\rho}[\operatorname{tr}(O\hat{\rho})]\leq\mathbb{E}_{\mathbb{U},\rho}[\operatorname{tr}(O\hat{\rho})^2]\leq\max_{\rho}\mathbb{E}_{\mathbb{U},\rho}[\operatorname{tr}(O\hat{\rho})^2]. \end{aligned}
其中 \max_\rho 表示遍历所有合法的密度矩阵取最大值。因此,这个上界是一个和所测量子态无关的量,只依赖于 O 和 \mathbb{U} ,(开根号后)称为 shadow norm,记作
\begin{aligned} \|O\|^2_{\text{shd}} = \max_{\rho}\mathbb{E}_{\mathbb{U},\rho}[\operatorname{tr}(O\hat{\rho})^2]. \end{aligned}
但这个取最大值一般难以计算,有时我们可以用最大混态代替(相当于取平均)[3],来近似表征上界的大小(也可以称为 shadow norm),记作
\begin{aligned} \|O\|^2_{\text{shd}} = \mathbb{E}_{\mathbb{U},I/d}[\operatorname{tr}(O\hat{\rho})^2] = \frac{\operatorname{tr}(O\mathcal{M}^{-1}(O))}{d}. \end{aligned}
这个量的计算非常简单,代入观测量和重构信道即可。
利用 shadow norm,可以证明,若用同一组数据同时求多个可观测量期望,经典影子层析的样本复杂度可以降低到[2]
\begin{aligned} \mathcal{O}\left(\frac{\log(K/\delta)}{\epsilon^2}\max_k\|O_k\|^2_{\text{shd}}\right), \end{aligned}
其中 K 表示需测的可观测量总数, O_k 表示第 k 个可观测量, \epsilon 表示容许误差, 1-\delta 表示成功概率。这个 sample scaling 达到了量子信息的理论下界[2]。
2.4 常用例子
最常用的随机测量方案是 Pauli 随机测量,对应的系综 \mathbb{U} 由每个 qubit 上独立的随机 Clifford 线路构成,对应的重构信道为
\begin{aligned} \mathcal{M}^{-1}_{\text{Pauli}}(\sigma)=\bigotimes_{n=1}^N (3\sigma_n-\operatorname{tr}(\sigma_n)I). \end{aligned}
其中 \sigma_n 对应 \sigma 在第 n 个 qubit 上的缩并指标,图示如下
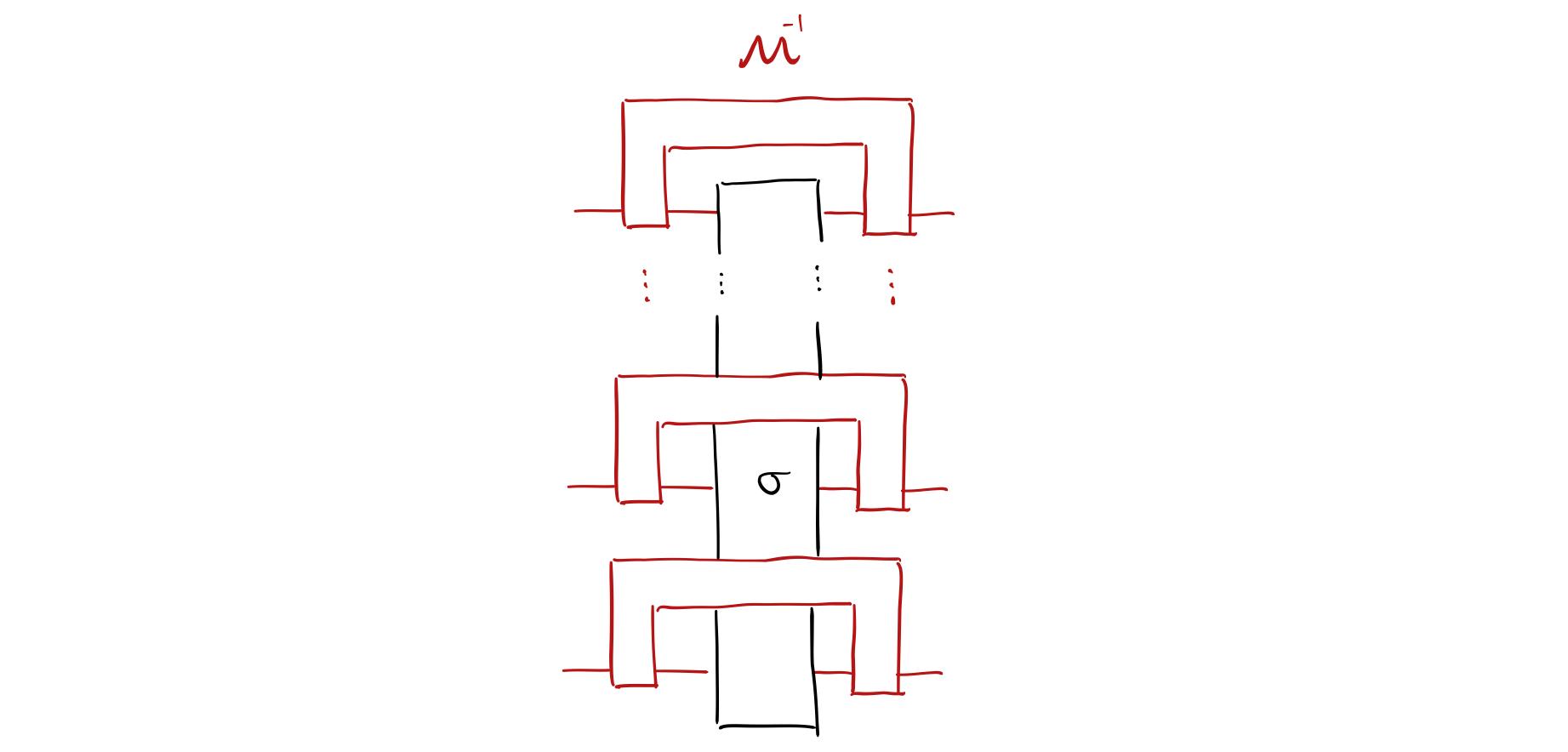
Tensor product structure of the reconstruction map for the Pauli randomized measurement.
注:此处图示含义可以参考:开放系统演化的张量网络图示。 Pauli 随机测量对于 Pauli string 的 shadow norm 为
\begin{aligned} \|P\|^2_{\text{shd}} = \frac{\operatorname{tr}(P\mathcal{M}^{-1}(P))}{d} = 3^l. \end{aligned}
此处 l 表示 P 的作用区域(support)。它不依赖于系统大小 N 。这意味着,Pauli 随机测量可以很好地给出少体观测量的期望值,例如局域序参量、两点关联函数等,因此也适合用来估计局域相互作用的哈密顿量的期望。
另一个常见的方案是 Clifford 随机测量,对应的系综是系统的整个 Clifford 群(3-design),对应的重构信道就是上节中 Haar 的重构信道。它对于一般观测量的 shadow norm 为
\begin{aligned} \|O\|^2_{\text{shd}} = \frac{\operatorname{tr}(O\mathcal{M}^{-1}(O))}{d} = \left(1+2^{-N}\right)\operatorname{tr}(O^2)-2^{-N}(\operatorname{tr}O)^2. \end{aligned}
它依赖于可观测量的 Schatten 2-norm,这意味着 Clifford 随机测量适用于估计保真度、纯度等全局但模较小的可观测量。
此外,介于两者之间的,可以使用有限深度的 Clifford 线路来做随机测量[4],相应的重构信道需要一些额外的经典计算。
<hr/>参考
原文地址:https://zhuanlan.zhihu.com/p/638536355 |
|
 /3
/3 