何为“层次分析法”？一把量化决策的利器！

奋斗的小鸟

层次分析法(Analytic Hierarchy Process，简称AHP)，是一种将影响决策的因素分解成目标、准则、方案等层次进行定性和定量分析的决策方法，在20世纪70年代由美国运筹学家托马斯·塞蒂(T.L.saaty)提出，现在已被广泛应用于经济、军事、农业、教育、医疗和环境等领域。
层次分析法与人的决策过程相似，以食堂就餐为例：有“西苑”“学苑”“北苑”3个食堂可供选择，L同学想根据一些准则来对它们进行比较，从中确定就餐的最佳地点，基本步骤如下：
一、建立层次结构

先将该问题分解为3个层次，最上层为目标层，即“选择食堂”，最下层为方案层，即“西苑”“学苑”“北苑”3个地点，中间为准则层，分为“距离远近”“菜品种类”“食物价格”“内部环境”和“拥挤情况”5个准则，各层之间的联系用相连的直线表示，如下图所示


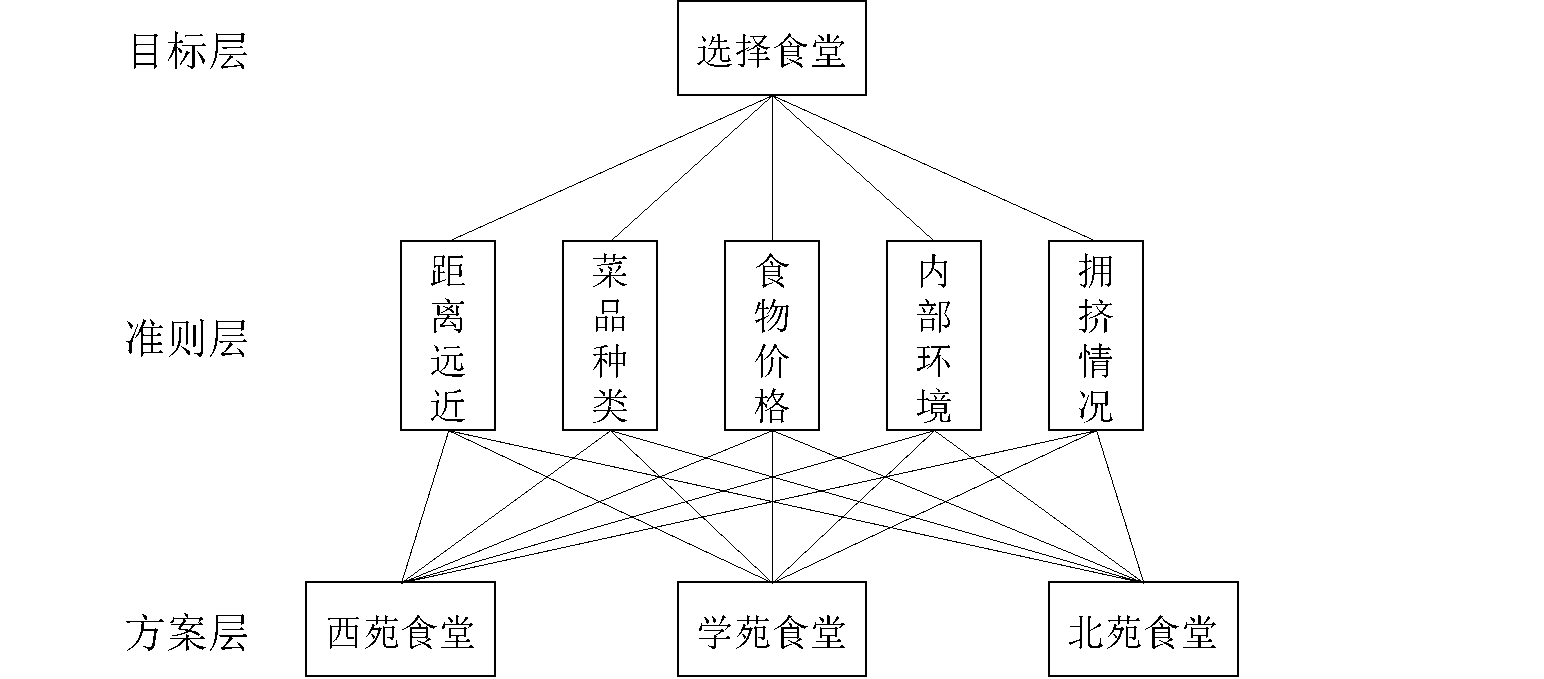
二、构造成对比较矩阵

由于影响决策的因素不易测量，人们凭借经验得到的结果也往往不准确。为了得到准则层对目标层的权重，列一个矩阵A=(a_{ij})_{5\times5}，其行属性C_i和列属性C_j分别代表5个准则，各元素a_{ij}通过C_i和C_j相互比较来确定。在进行成对比较时，通常采用如下1-9尺度\begin{array}{c|l} \hline \text{尺度}a_{ij} & \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{含义}\\ \hline 1 & C_i\text{与}C_j\text{的影响相同}\\ 3 & C_i\text{比}C_j\text{的影响稍强}\\ 5 & C_i\text{比}C_j\text{的影响强}\\ 7 & C_i\text{比}C_j\text{的影响明显的强}\\ 9 & C_i\text{比}C_j\text{的影响绝对的强}\\ 2,4,6,8 & C_i\text{与}C_j\text{的影响之比在上述两个相邻等级之间}\\ 1,\frac{1}{2},\ldots,\frac{1}{9} & C_i\text{与}C_j\text{的影响之比为上面}a_{ij}\text{的互反数}\\ \hline \end{array}\\以“距离远近”与其他准则的比较为例：L同学认为，“距离远近”的重要性与自身相同，比“菜品种类”明显的弱，比“食物价格”“内部环境”弱，比“拥挤情况”稍弱。根据1-9尺度，A的第一行元素为1,\frac{1}{7},\frac{1}{5},\frac{1}{5},\frac{1}{3}，其他行元素同理，可得到如下成对比较矩阵


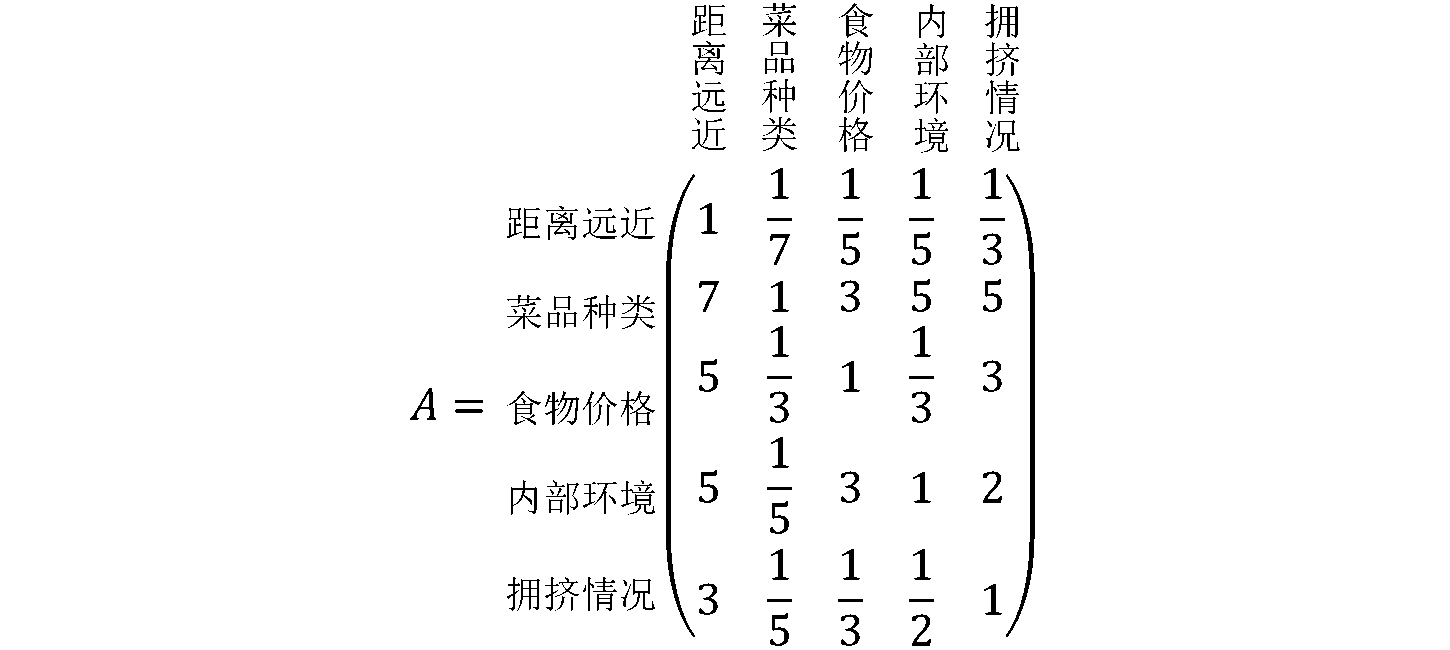
三、计算权向量，并做一致性检验

矩阵A的元素都是正数，且关于对角线对称的元素互为倒数，称为正互反矩阵。对于正互反阵，利用和法[1]等实用简便算法，可近似计算A的最大特征值为\lambda^{(2)}=5.4286,\\归一化的特征向量为\vec{w}^{(2)}=(0.0416,0.4833,0.1721,0.2123,0.0906)^\mathrm{T},\\即得到5个准则对目标的权重，称向量\vec{w}^{(2)}为第2层对上一层的权向量。可以证明[1]，用特征向量作权向量优于用其他方法得到的权向量。
权向量的含义为：该层诸因素对上一层因素的权重大小。从\vec{w}^{(2)}可知，5个准则按重要程度排序是：“菜品种类”居首位，“内部环境”次之，再者是“食物价格”，最后是“拥挤情况”和“距离远近”，L同学的“吃货”属性可见一斑！
由于矩阵A通过行列属性两两比较得到，可能出现诸如“甲优于乙，乙优于丙，丙优于甲”等成对比较不一致的情况，因此，需要做一致性检验：先计算一致性指标CI^{(2)}=\frac{\lambda^{(2)}-n_A}{n_A-1}=0.1072,\\其中，n_A为矩阵A的阶数。再根据如下随机一致性指标RI的数值表\begin{array}{c|ccccccccccc} \hline n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\ \hline RI & 0 & 0 & 0.58 & 0.90 & 1.12 & 1.24 & 1.32 & 1.41 & 1.45 & 1.49 & 1.51\\ \hline \end{array}计算一致性比率CR^{(2)}=\frac{CI^{(2)}}{RI^{(2)}}=0.0957<0.1,\\矩阵A的不一致程度在可容许范围内（0.1的选取带有一定主观信度），通过一致性检验。否则，需要重新构造成对比较矩阵。
四、计算组合权向量，并做组合一致性检验

用同样的方法构造方案层对准则层的成对比较矩阵。以方案层对“距离远近”的比较为例：“西苑”比“学苑”稍近，比“北苑”稍远；“学苑”比“北苑”远。根据1-9尺度，得到如下成对比较矩阵


同理得到方案层对“菜品种类”“食物价格”“内部环境”“拥挤情况”的成对比较矩阵B_2=\begin{pmatrix} 1 & 3 & 7\\ \frac{1}{3} & 1 & 5\\ \frac{1}{7} & \frac{1}{5} & 1 \end{pmatrix}, B_3=\begin{pmatrix} 1 & 1 & \frac{1}{3}\\ 1 & 1 & \frac{1}{3}\\ 3 & 3 & 1 \end{pmatrix},\\ B_4=\begin{pmatrix} 1 & 3 & 9\\ \frac{1}{3} & 1 & 7\\ \frac{1}{9} & \frac{1}{7} & 1 \end{pmatrix}, B_5=\begin{pmatrix} 1 & 3 & \frac{1}{3}\\ \frac{1}{3} & 1 & \frac{1}{5}\\ 3 & 5 & 1 \end{pmatrix},\\同样计算第3层对上一层的成对比较矩阵B_k的权向量\vec{w}_k^{(3)}、最大特征根\lambda_k^{(3)}、一致性指标CI_k^{(3)}和一致性比率CR_k^{(3)}，结果如下表所示\begin{array}{c|ccccc} \hline k & 1 & 2 & 3 & 4 & 5\\ \hline  & 0.2605 & 0.6434 & 0.2000 & 0.6486 & 0.2605\\ \vec{w}_k^{(3)} & 0.1062 & 0.2828 & 0.2000 & 0.2946 & 0.1062\\  & 0.6333 & 0.0738 & 0.6000 & 0.0567 & 0.6333\\ \hline \lambda_k^{(3)} & 3.0387 & 3.0655 & 3.0000 & 3.0813 & 3.0387\\ \hline CI_k^{(3)} & 0.0194 & 0.0328 & 0.0000 & 0.0406 & 0.0194\\ \hline CR_k^{(3)} & 0.0334 & 0.0565 & 0.0000 & 0.0701 & 0.0334\\ \hline \end{array}\\上述B_k均通过一致性检验。
目前已经得到第2层对第1层的权向量\vec{w}^{(2)}=(0.0416,0.4833,0.1721,0.2123,0.0906)^\mathrm{T},\\以及第3层对第2层的权向量构成的矩阵\begin{align} W^{(3)} &=(\vec{w}_1^{(3)},\vec{w}_2^{(3)},\vec{w}_3^{(3)},\vec{w}_4^{(3)},\vec{w}_5^{(3)})\\ &=\begin{pmatrix} 0.2605 & 0.6434 & 0.2000 & 0.6486 & 0.2605\\ 0.1062 & 0.2828 & 0.2000 & 0.2946 & 0.1062\\ 0.6333 & 0.0738 & 0.6000 & 0.0567 & 0.6333 \end{pmatrix},\\ \end{align}则第3层对第1层的组合权向量为\vec{w}^{(3)}=W^{(3)}\vec{w}^{(2)}=(0.5176,0.2477,0.2347)^\mathrm{T},\\结果表明，“西苑”在“选择食堂”中所占的权重远高于“学苑”和“北苑”，故应作为第一选择地点。
除了要对每个成对比较矩阵进行一致性检验，还要进行组合一致性检验：定义CI^{(3)}=(CI_1^{(3)},CI_2^{(3)},CI_3^{(3)},CI_4^{(3)},CI_5^{(3)})\vec{w}^{(2)}=0.0270,\\则第3层的组合一致性比率为CR^{(3)}=\frac{CI^{(3)}}{RI^{(3)}}=0.0466<0.1,\\故第3层通过组合一致性检验。再定义第3层对第1层的组合一致性比率为CR^{\star}=\sum_{p=2}^{3}{CR^{(p)}}=0.1423,\\当CR^{\star}适当小时，认为整个层次的比较判断通过一致性检验，前面得到的组合权向量\vec{w}^{(3)}可以作为最终决策的依据。
Matlab的实现代码如下：
function [w,lambda,CI,CR] = AHP(A)
    %% 和法
    n = length(A);
    W_tilde = A/diag(sum(A));   % a.列归一化
    w_tilde = sum(W_tilde,2);   % b.行求和
    w = w_tilde/sum(w_tilde);   % c.特征向量
    lambda = 1/n*sum(A*w./w);   % d.特征值
    %% 一致性检验
    CI = (lambda-n)/(n-1);   % 一致性指标
    RI = [0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];   % 随机一致性指标
    CR = CI/RI(n);   % 一致性比率
end接下来，就层次分析法的应用做进一步讨论：
A. 组合权向量的计算公式的由来

将原层次结构中的直线消去，各层之间的联系用它们的相对位置表示，权向量\vec{w}^{(2)}和\vec{w}_{k}^{(3)}的各元素写在对应因素的下方，如下图所示


例如，要计算方案层的“西苑食堂”对目标层的总权重，就是要将“西苑食堂”对各个准则进行加权求和，即\begin{align} &\color{red}{0.2605}\times\color{blue}{0.0416}+\color{red}{0.6434}\times\color{blue}{0.4833}+\color{red}{0.2000}\times\color{blue}{0.1721}\\ &+\color{red}{0.6486}\times\color{blue}{0.2123}+\color{red}{0.2605}\times\color{blue}{0.0906}=\color{orange}{0.5176},\\ \end{align}用矩阵表示为\begin{pmatrix} \color{red}{0.2605} & \color{red}{0.6434} & \color{red}{0.2000} & \color{red}{0.6486} & \color{red}{0.2605}\\ 0.1062 & 0.2828 & 0.2000 & 0.2946 & 0.1062\\ 0.6333 & 0.0738 & 0.6000 & 0.0567 & 0.6333 \end{pmatrix} \begin{pmatrix} \color{blue}{0.0416}\\ \color{blue}{0.4833}\\ \color{blue}{0.1721}\\ \color{blue}{0.2123}\\ \color{blue}{0.0906} \end{pmatrix} = \begin{pmatrix} \color{orange}{0.5176}\\ 0.2477\\ 0.2347 \end{pmatrix},\\由此可见，组合权向量的计算，本质上实现了权重的再分配。这就是公式\vec{w}^{(3)}=W^{(3)}\vec{w}^{(2)}的由来。
B. 群体决策的情况

当多人通过层次分析法处理问题时，要用一定的方法，集结个人偏好，凝聚群体智慧，得到决策结果。集结方法有两类[2]：一类是对成对比较矩阵集结，如加权几何平均成对比较矩阵法、加权算术平均成对比较矩阵法；一类是对权向量集结，如加权几何平均权向量法、加权算术平均权向量法。四种集结方法各有优劣，当决策量较大时，第二类比第一类具有明显的计算优势，也不存在保持成对比较矩阵的互反性、一致性方面的困难，因此更为常用。
例如，L同学想在“西苑”“学苑”“北苑”中选择一个食堂就餐，他用层次分析法得到的权向量为\vec{w}_1=(0.5176,0.2477,0.2347)^\mathrm{T},\\M、N同学也想和L同学一同就餐，他们分别用层次分析法得到的权向量为\vec{w}_2=(0.3658,0.4366,0.1976)^\mathrm{T},\\ \vec{w}_3=(0.2434,0.3399,0.4167)^\mathrm{T},\\三人的话语权重为0.4,0.3,0.3。若采用加权算术平均权向量法，则群决策的结果为\vec{w}=0.4\vec{w}_1+0.3\vec{w}_2+0.3\vec{w}_3=(0.3898,0.3320,0.2782)^\mathrm{T},\\因此，三人应当一同前往“西苑”。
C. 存在子准则层的情况

上一层的某些因素只支配下一层的部分因素的层次结构，称为不完全的。当存在多个准则层时，若不完全性只发生在各准则层之间，此时可以先将不支配的那些因素的权向量分量置0，再进行后续的计算[1]。
例如，“菜品种类”再分为“素菜”和“荤菜”，“内部环境”再分为“装潢”和“卫生”。为了方便用矩阵的观点进行计算，将其余准则也写入其对应的子准则中（用虚线加以区分），如下图所示


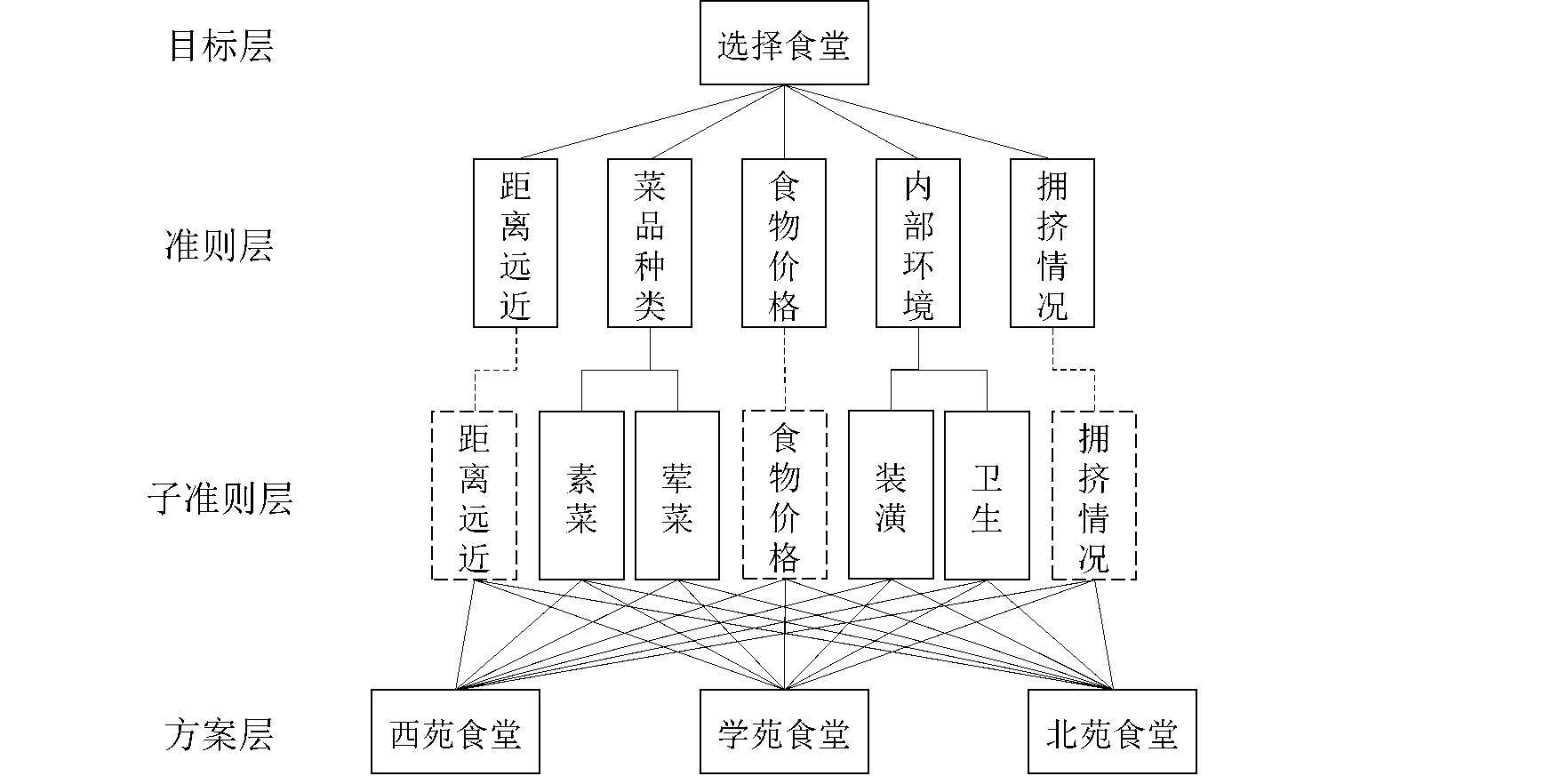
设准则层对目标层的权向量为\vec{w}^{(2)}，子准则对5个准则的权向量为\vec{w}_k^{(3)}(k=1,2,\ldots,5)。子准则有7个，故\vec{w}_k^{(3)}是7维列向量。而“距离远近”只与其子准则“距离远近”有关，故\vec{w}_1^{(3)}=(1,0,0,0,0,0,0)^\mathrm{T},\\“菜品种类”只与其子准则“素菜”“荤菜”有关，故\vec{w}_2^{(3)}=(0,w_1,w_2,0,0,0,0)^\mathrm{T},\\其中，w_1和w_2由“素菜”“荤菜”对“菜品种类”的成对比较矩阵得到，其余\vec{w}_k^{(3)}同理，则子准则层对准则层的权向量构成的矩阵为W^{(3)}=(\vec{w}_1^{(3)},\vec{w}_2^{(3)},\vec{w}_3^{(3)},\vec{w}_4^{(3)},\vec{w}_5^{(3)}),\\因此，子准则层对目标层的组合权向量为\vec{w}^{(3)}=W^{(3)}\vec{w}^{(2)},\\再用常规做法计算各方案对7个子准则的权向量\vec{w}_k^{(4)}(k=1,2,\ldots,7)，它们分别由方案层对7个子准则的成对比较矩阵得到，则方案层对子准则层的权向量构成的矩阵为W^{(4)}=(\vec{w}_1^{(4)},\vec{w}_2^{(4)},\vec{w}_3^{(4)},\vec{w}_4^{(4)},\vec{w}_5^{(4)},\vec{w}_6^{(4)},\vec{w}_7^{(4)}),\\因此，方案层对目标层的组合权向量为\vec{w}^{(4)}=W^{(4)}\vec{w}^{(3)}.\\
D. 成对比较矩阵残缺的情况

由于某些原因，无法给出某两个因素相互对比的结果a_{ij}时，就使成对比较矩阵出现残缺。当残缺阵A为不可约矩阵[3]时，可用修正阵\tilde{A}代替残缺阵A。修正阵\tilde{A}的构造方法为：\tilde{a}_{ij}= \begin{cases} a_{ij},\ \ \ \ \ \ \ \ \ \ a_{ij}\text{未缺失},\ i\ne j\\ 0,\ \ \ \ \ \ \ \ \ \ \ \ \ a_{ij}\text{已缺失},\ i\ne j\\ m_i+1,\ \ \ m_i\text{为第}i\text{行缺失元素的个数},\ i=j \end{cases}\\例如，在构造3个食堂对“距离远近”的成对比较矩阵时，L同学觉得“西苑”与“学苑”的距离不好比较，于是得到B_1= \begin{pmatrix} 1 & \text{?} & \frac{1}{3}\\ \text{?} & 1 & \frac{1}{5}\\ 3 & 5 & 1 \end{pmatrix},\\此时可将缺失阵B_1修正为\tilde{B}_1= \begin{pmatrix} \color{red}{2} & \color{blue}{0} & \frac{1}{3}\\ \color{blue}{0} & \color{red}{2} & \frac{1}{5}\\ 3 & 5 & 1 \end{pmatrix},\\计算得到的权向量为\vec{\tilde{w}}_1^{(3)}=(0.2058,0.1387,0.6555)^\mathrm{T},\\与矩阵B_1完整时得到的权向量\vec{w}_1^{(3)}=(0.2605,0.1062,0.6333)^\mathrm{T},\\是十分接近的，原因在于缺失的元素a_{12}可以通过a_{13}和a_{32}间接估计得到。
E. 与其他评价方法相结合

当方案数较多时，用成对比较矩阵计算权向量的代价很大，可考虑方案直接对准则进行量化和评估。例如，“距离远近”用长度表示，“菜品种类”用种类数目表示，“食物价格”用平均价格表示，“内部环境”用满意度表示，“拥挤情况”用人流密度表示。现在考虑7个食堂对5个准则的评估结果，如下表所示（虚拟数据）\begin{array}{|c|c|c|c|c|c|} \hline  & \text{距离远近} & \text{菜品种类} & \text{食物价格} & \text{内部环境} & \text{拥挤情况}\\  & \text{/米} & \text{/种} & \text{/元} & \text{/分} & \text{/(人/米}^2\text{)}\\ \hline \text{西苑} & 500 & 120 & 20 & 85 & 4.2\\ \hline \text{学苑} & 550 & 100 & 20 & 70 & 4.7\\ \hline \text{北苑} & 100 & 80 & 10 & 60 & 3.8\\ \hline \text{南苑} & 850 & 80 & 10 & 65 & 3.6\\ \hline \text{东苑} & 1500 & 60 & 20 & 80 & 2.3\\ \hline \text{三好坞} & 450 & 40 & 30 & 85 & 2.1\\ \hline \text{半亩园} & 550 & 40 & 50 & 90 & 1.8\\ \hline \end{array}\\这就构成了决策矩阵C=(c_{ij})_{7\times5}，但它的列属性在类型、值域和量纲上各不相同，因此还要进行属性规范化，常用方法有线性变换法、极差变换法、向量规范化、向量标准化等[4]。
以极差变换法为例：“菜品种类”“内部环境”属于效益型属性（值越大越好），令\tilde{c}_{ij}=\frac{c_{ij}-c_j^\min}{c_j^\max-c_j^\min},\\而“距离远近”“食物价格”“拥挤情况”属于成本型属性（值越小越好），令\tilde{c}_{ij}=\frac{c_j^\max-c_{ij}}{c_j^\max-c_j^\min},\\每个属性经过变换的最优值为1、最差值为0，其余值均在[0,1]上，且消除了量纲效应，可得到如下规范化决策矩阵\tilde{C}=(\tilde{c}_{ij})_{7\times5}\begin{array}{|c|c|c|c|c|c|} \hline  & \text{距离远近} & \text{菜品种类} & \text{食物价格} & \text{内部环境} & \text{拥挤情况}\\  & \text{/米} & \text{/种} & \text{/元} & \text{/分} & \text{/(人/米}^2\text{)}\\ \hline \text{西苑} & 0.7143 & \color{red}{1.0000} & 0.7500 & 0.8333 & 0.1724\\ \hline \text{学苑} & 0.6786 & 0.7500 & 0.7500 & 0.3333 & \color{blue}{0.0000}\\ \hline \text{北苑} & \color{red}{1.0000} & 0.5000 & \color{red}{1.0000} & \color{blue}{0.0000} & 0.3103\\ \hline \text{南苑} & 0.4643 & 0.5000 & \color{red}{1.0000} & 0.1667 & 0.3793\\ \hline \text{东苑} & \color{blue}{0.0000} & 0.2500 & 0.7500 & 0.6667 & 0.8276\\ \hline \text{三好坞} & 0.7500 & \color{blue}{0.0000} & 0.5000 & 0.8333 & 0.8966\\ \hline \text{半亩园} & 0.6786 & \color{blue}{0.0000} & \color{blue}{0.0000} & \color{red}{1.0000} & \color{red}{1.0000}\\ \hline \end{array}\\再结合其他评价方法，可得到方案层对目标层的权重，如关注数据位置关系的理想解法[4]、关注曲线态势变化的灰色关联分析法[4]、关注秩统计量的秩和比法[4]、关注事物特征量值的物元分析法[5]、关注信息无序度的熵值分析法[6]，等等。
最后，来谈一谈层次分析法的优缺点：
• 层次分析法的优点

• 系统性。它把研究对象作为一个系统，按照分解比较、判断综合的思维方式进行决策，成为继机理分析、统计分析之后的系统分析的重要工具。
  
• 实用性。它把定性和定量方法相结合，应用范围广，能够处理许多用传统的最优化技术无法着手的实际问题。
  
• 简洁性。计算简便，结果明确，一般人都能了解它的基本原理和掌握它的基本步骤。
  

• 层次分析法的缺点

• 只能从既有方案中选优，不能生成新方案。
  
• 通过比较判断得到的结果相对粗糙，不适于处理高精度问题。
  
• 从建立层次结构模型到构造成对比较矩阵，人的主观因素的作用很大，可能使决策结果难以为众人接受。
  

参考

• ^abc姜启源, 谢金星, 叶俊. 数学模型(第四版)[M]. 北京: 高等教育出版社, 2011: 263-264, 264-266, 266-267.
  
• ^朱心想. 群决策过程中层次分析法的研究与应用[D]. 北京理工大学, 2003.
  
• ^Wan F Y M(温耀明). Mathematical Models and Their Analysis. Harper & Row Pub. , 1989.
  
• ^abcd司守奎, 孙玺菁. 数学建模算法与应用(第2版)[M]. 北京: 国防工业出版社, 2017: 371-373, 369-375, 384-387, 390-393.
  
• ^李博, 庄弘炜, 赵法栋, 庄维伟. 模糊物元分析在军事装备退役决策中的应用[J]. 火力与指挥控制, 2014(6): 167-169.
  
• ^刘瑾, 冯瑛敏, 章辉, 冯亮, 孙瑞雪, 王丽珠. 基于熵值分析和层次分析法的智能电网电力终端接入网综合效益评价[J]. 电力建设, 2015(5): 137-140.
  

原文地址：https://zhuanlan.zhihu.com/p/94299606