有哪些有效的可以衡量两段或多段时间序列相似度的方法？

大v

现有的time series similarity的常用衡量方法有Euclidean Distance, DTW等，请问还有哪些各领域中应用比较有效的衡量方法或者相关的paper，以及常用的preprocessing方法如wavelet, kalman filter等是否能够提高计算精度呢。

原文地址：https://www.zhihu.com/question/281783839

清风寡欲

最近在大量阅读时间序列挖掘相关的文献，今天特意系统性地回答一下这个问题。此回答主要做一个系统性科普，不会涉及太多数学/统计的细节。本回答的结构安排如下。

• 一个好的相似度度量方法(Similarity Measure)需要具备哪些好的性质？
  
• 现有的时间序列相似度度量方法(Time Series Similarity Measure)分类以及简要介绍？
  
• 现有的时间序列相似度度量方法(Time Series Similarity Measure)总结？
  

<hr/>第一节：一个好的相似度度量方法(Similarity Measure)需要具备哪些好的性质？

备注: 我这里说的Similarity Measure是指一般的相似度度量，而不局限于时间序列相似度度量(Time Series Similarity Measure).

• Similarity Measure能够识别在感觉上比较相似、但是在数学意义上不完全一样的物体。比如说下图中的叶子哪一些比较相似？因为世界上没有两片一模一样的叶子，所以一个好的相似度度量方法需要能够识别感觉上/直观上比较相似的叶子。
  

source: [1]

2. Similarity Measure的结果应该和人类的直觉相符合。如果你告诉我上图中的枫叶和扇形叶子的形状很相似，那我只能说你在扯蛋。
3. Similarity Measure, 不管在全局(global)，还是局部(local)水平上，都应该重点关注一个物体的显著特征，而不是鸡毛蒜皮的无关细节。比如说，你告诉我上图中的枫叶和扇形叶子很相似，因为它们的边缘都是呈现小锯齿状(local feature)。你也告诉我，上图中的两片扇形叶子很相似，因为它们都是扇形(global feature)。我都会觉得你说得有道理。 但是如果你告诉我，上图中的枫叶和扇形叶子很相似，因为它们上面都有泥巴，我只能说“我不关心这个”。
上面三点描述的是通用的Similarity Measure，现在来讨论Time Series Similarity Measure.
4. 除了以上的通用方面外，对于一个好的Time Series Similarity Measure来讲，它应该能够比较两个长度不相等的时间序列。(然而，如果两条时间序列长度相差太大，计算它们的相似度也会变得没有意义[2])
5. 一个好的Time Series Similarity Measure的复杂度应该越低越好。换句话说，Time Complexity 和 Space Complexity 都要小。
6. 一个好的Time Series Similarity Measure应该对各种扭曲(distortion)和变换(transformation)不敏感。具体有哪些distortion和transformation呢？具体见下图。



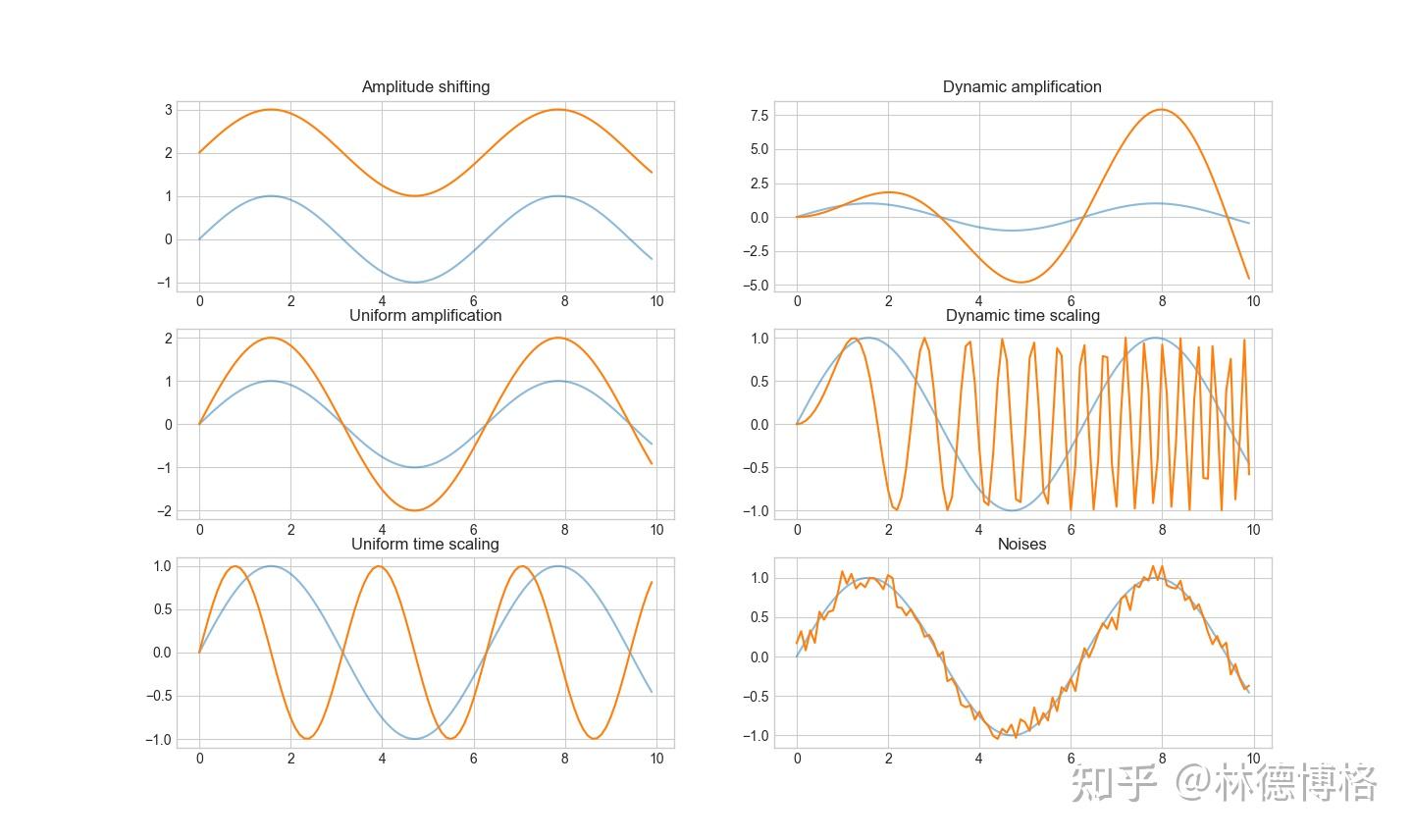
蓝色代表原始时间序列，橙色代表扭曲或者变换之后的时间序列

在理想情况下，上面六对时间序列应该被看作是相似的。也就是说，一个好的Time Series Similarity Measure应该对这些扭曲和变换不敏感。
"""
用于复现上述distortion, transformation 的python代码
Created on Fri Mar  4 10:01:27 2022
@author: zlifr
““”
import numpy as np
import matplotlib.pyplot as plt
fig, axs = plt.subplots(3,2)

##Raw time series
time = np.arange(0, 10, 0.1);
amplitude  = np.sin(time)

axs[0,0].plot(time, amplitude, alpha = 0.5)
axs[1,0].plot(time, amplitude, alpha = 0.5)
axs[2,0].plot(time, amplitude, alpha = 0.5)
axs[0,1].plot(time, amplitude, alpha = 0.5)
axs[1,1].plot(time, amplitude, alpha = 0.5)
axs[2,1].plot(time, amplitude, alpha = 0.5)

##Amplitude shifting
time = np.arange(0, 10, 0.1);
amplitude  = np.sin(time)+2
axs[0,0].plot(time, amplitude)
axs[0,0].set_title("Amplitude shifting")

##Uniform amplification
time = np.arange(0, 10, 0.1);
amplitude  = np.sin(time)*2
axs[1,0].plot(time, amplitude)
axs[1,0].set_title("Uniform amplification")

##Uniform time scaling
time = np.arange(0, 10, 0.1);
amplitude  = np.sin(time*2)
axs[2,0].plot(time, amplitude)
axs[2,0].set_title("Uniform time scaling")

##Dynamic amplification
time = np.arange(0, 10, 0.1);
amplitude  = np.sin(time)*time
axs[0,1].plot(time, amplitude)
axs[0,1].set_title("Dynamic amplification")

##Dynamic time scaling
time = np.arange(0, 10, 0.1);
amplitude  = np.sin(time*time)
axs[1,1].plot(time, amplitude)
axs[1,1].set_title("Dynamic time scaling")

##Noises
time = np.arange(0, 10, 0.1);
amplitude  = np.sin(time)+np.random.normal(0,0.1,100)
axs[2,1].plot(time, amplitude)
axs[2,1].set_title("Noises")<hr/>第二节：现有的时间序列相似度度量方法(Time Series Similarity Measure)分类以及简要介绍？

Time Series Similarity Measure大概可以分为四类：

• 基于形状的(Shape Based Time Series Similarity Measure)
  
• 基于编辑距离的(Edit Based Time Series Similarity Measure)
  
• 基于特征的(Feature Based Time Series Similarity Measure)
  
• 基于结构的(Structure Based Time Series Similarity Measure)
  

• Shape Based Time Series Similarity Measure
  

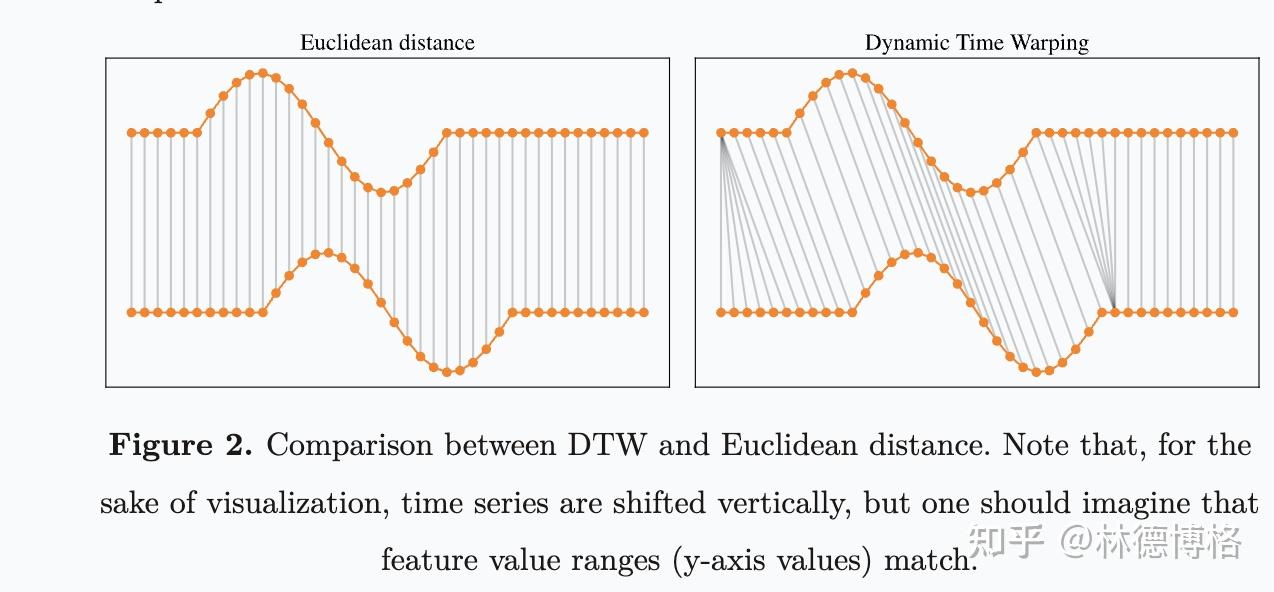
欧几里得距离和DTW距离比较(source:  https://rtavenar.github.io/blog/dtw.html)

这一类方法的基本思想是，通过比较时间序列的整体形状来计算相似度。这一类方法包括了大名鼎鼎的Euclidean distance 和 DTW。
主要包括以下方法：

• Euclidean Distance and other norms.
  
• Dynamic Time Warping (DTW)
  
• LB-Keogh (variant of DTW)
  
• Spatial  Assembling (SpADe)
  
• Optimal Bijection (OSB)
  
• DISSIM
  

2. Edit Based Time Series Similarity Measure



Longest Common Subsequence （source: https://www.enjoyalgorithms.com/blog/longest-common-subsequence ）

这一类方法的基本思想是，通过计算“最少需要多少步基本操作来把一段时间序列变成另外一段时间序列”来衡量相似度。举个例子，给定两个序列：ABC，ABD，以及三个基本操作“删除、添加、替换”，我们最少需要一个基本操作“替换”(C替换成D)，将ABC编程ABD. 主要包括以下方法：

• Levenshtein
  
• Weighted Levenshtein
  
• Edit with Real Penalty (ERP)
  
• Time Warp Edit Distance (TWED)
  
• Longest Common SubSeq (LCSS)
  
• Sequence Weighted Align (Swale)
  
• Edit Distance on Real(EDR)
  
• Extended Edit Distance(EED)
  
• Constraint Continuous  Edit(CCED)
  

3. Feature Based Time Series Similarity Measure



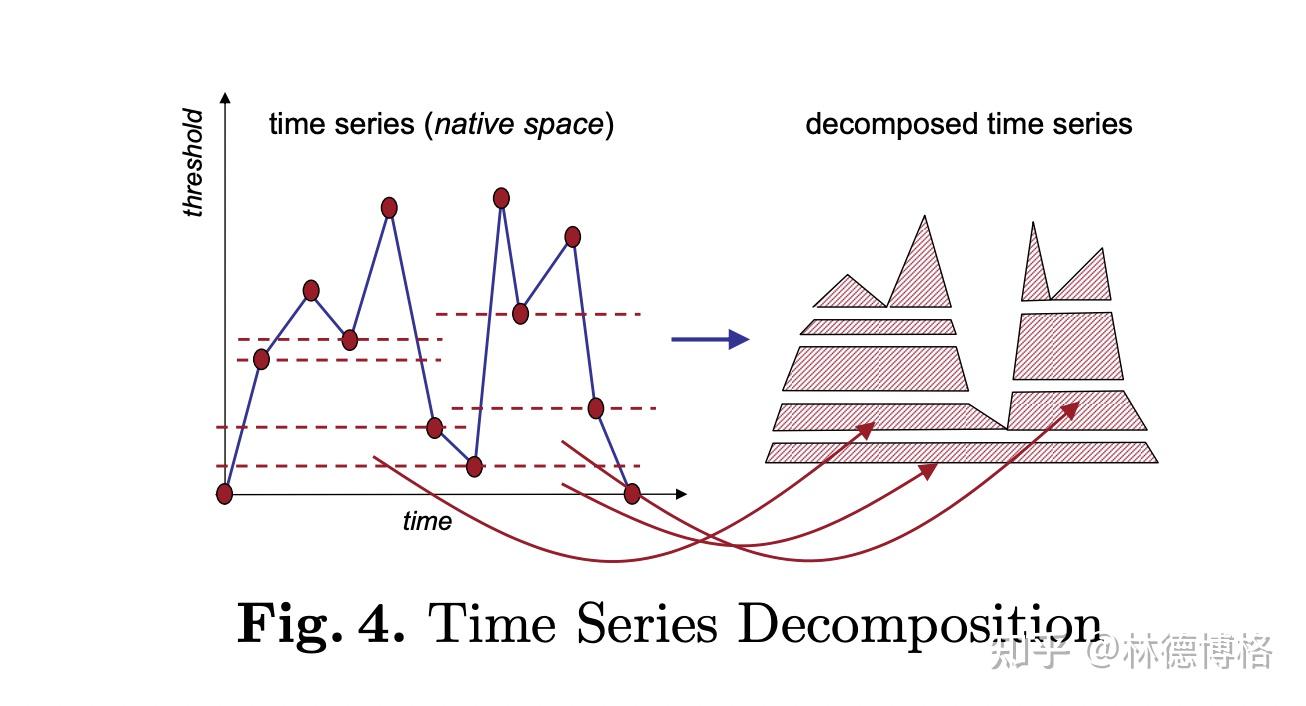
TQuest Distance(source: https://www.dbs.ifi.lmu.de/Publikationen/Papers/paper-edbt06_final.pdf)

这一类方法的基本思想是：首先提取出时间序列的特征，比如说统计学特征(最大值、最小值、均值，方差等)，或者是通过FFT提取出Amplitude, Energy, Phase, Damping Ratio, Frequency)等特征，然后直接计算这些特征之间的Eclidean distance 然后再求和。主要包括以下方法(也就是不同的特征提取和比较方法)：

• Likelihood
  
• Autocorrelation
  
• Vector quantization
  
• Threshold Queries (TQuest)
  
• Random Vectors
  
• Histogram
  
• WARP
  

4. Structure Based Time Series Similarity Measure
之前介绍的三种时间序列相似度度量方法适用于短的时间序列，然而对于较长的时间序列(比如说几万个点的时间序列)，前面三大类方法很可能会失效。于是，就有了第四类方法。前面三大类方法之所以失效，是因为它们过多关注局部特征(local feature)，而忽略了全局特征(Global feature)。而第四类方法的基本思想是：关注全局特征。
这一类方法可以进一步分为两类：基于模型的(model-based distance) 和 基于压缩的(Compression-based distance).
Model-based distance假设时间序列服从某个分布/模型，然后估计模型参数，最后通过比较模型参数之间的差异来反映时间序列的相似度。主要包括以下方法：

• Markov Chain(MC)
  
• Hidden Markov Models(HMM)
  
• Auto-Regressive(ARMA)
  
• Kullback-Leibler
  

Compression-based distance通过研究两个时间序列在一起压缩的压缩率来反映相似度。直观上，如果两个时间序列比较相似，则它们在一起压缩就比较容易。

• Compression Dissimilarity(CDM)
  
• Parsing-Based
  

第三节：现有的时间序列相似度度量方法(Time Series Similarity Measure)总结？

对于绝大部分同学来说，可能只知道Euclidean Distance的存在，更厉害一点的同学也知道DTW，或者还有LCSS. 然后，根据上面的梳理，大家可以看到，现有的时间序列相似度度量十分丰富，那么该如何选呢？这要取决于你的数据类型，以及你应用的领域。大体来说，根据[3]，可以给出以下几条建议：

• 如果你的时间序列比较短，并且通过双眼就能感觉出两个时间序列是否相似，那么建议选第一类方法Shape Based Time Series Similarity Measure.
  
• 如果你的时间序列的类型比较特殊，或者你有关于时间序列的一部分先验知识(比如说时间序列服从模型)，那么你可以选择第四类方法Structure Based Time Series Similarity Measure里面的model-based distance.
  
• 如果你的时间序列比较长，并且你对于时间序列本身一无所知。那么你可以考虑第四类方法Structure Based Time Series Similarity Measure里面的Compression-based distance.
  
• 如果你什么都不知道的话：如果你的时间序列是等长的，那么你可以用Euclidean Distance，DTW(大众的选择)。特别的，DTW的改进版本FastDTW计算起来也很快; 如果你的时间序列不是等长的，那么建议你选DTW.
  
• 此外，如果你要发论文，当选择一个时间序列相似度的时候，你需要考虑它是不是一个metric，以及它是否lower bound真实距离(不懂的同学可以直接跳过)。
  

最后放出一张总结表(感兴趣的同学可以去读原论文[3]，找每一个方法的参考文献)：



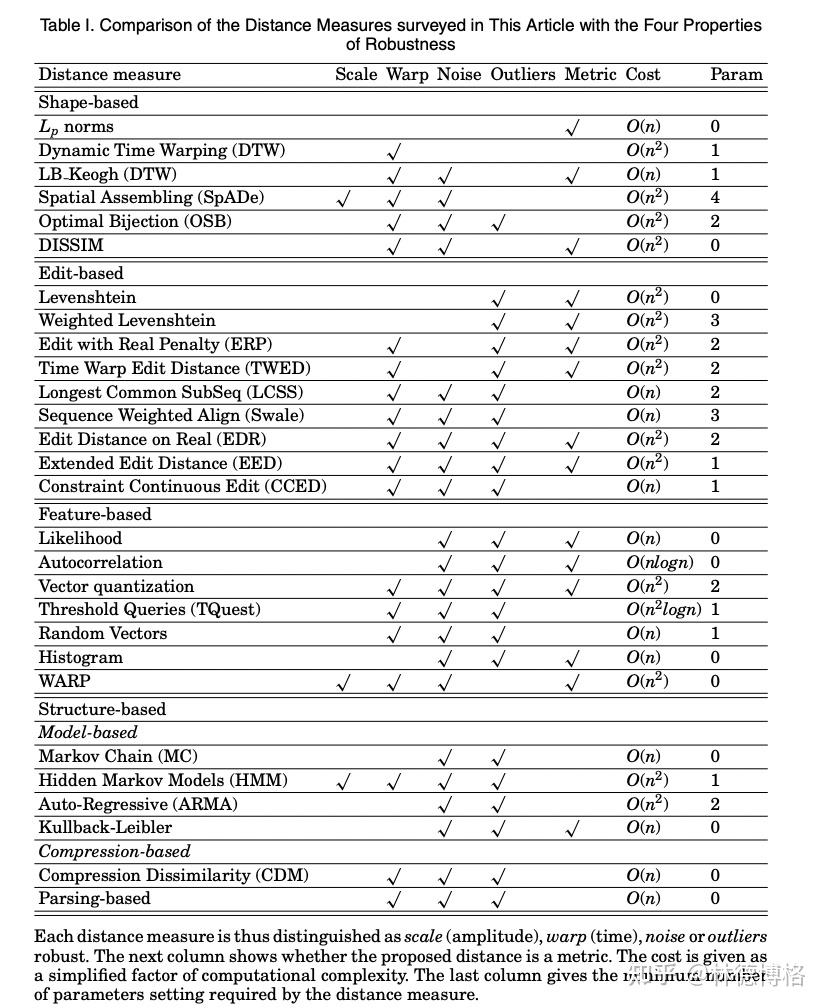
Source: [3]

<hr/>参考文献

[1] [PDF] Comparison of Leaf Recognition by Moments and Fourier Descriptors | Semantic Scholar
[2] Keogh Eamonn
[3] Esling, Philippe, and Carlos Agon. "Time-series data mining."ACM Computing Surveys (CSUR)45.1 (2012): 1-34.

同花顺

最近写了一篇文章，时间序列相似性的判断方法其实还挺多的，除了 Euclidean Distance，DTW 之外，还有挺多的判断方法。
时间序列的相似性
原文链接：时间序列的相似性
在文本挖掘中，可以通过 Word2Vec 生成的向量以及向量的内积，或者根据语义和词性来判断两个词语是否是近义词。在时间序列的挖掘中，同样可以找到一些方法来描述两条时间序列是否相似。
在介绍时间序列的距离之前，笔者感觉需要回顾一下数学中度量空间和内积空间的定义。
度量空间

在数学里面，集合 上的距离函数定义为 ，其中 表示实数集合，并且函数 满足以下几个条件：

• ，并且 当且仅当 ;
  
• ，也就是满足对称性；
  
• ，也就是三角不等式。
  

满足这三个条件的距离函数称为度量，具有某种度量的集合则叫做度量空间。
Remark.
在本文下面的时间序列距离的各种定义中，这些距离不一定满足三角不等式。例如动态时间算法（DTW）就不满足三角不等式。
内积空间

一个内积空间是域 （其中 或者 ）上的向量空间 与一个内积（映射）所构成， 上的一个内积定义为正定，非退化的共轭双线性形式，记成 ，它满足以下设定：
1. 对于任意的 ，有
2. 共轭双线性形式指的是：




3. 非负性：
4. 非退化：从 到对偶空间 的映射： 是同构映射。
基于欧几里德距离的相似度计算

假设两条时间序列曲线为 和 ，于是可以使用欧几里德空间里面的 范数来表示两个时间序列之间的距离。用公式来描述就是：




基于相关性的相似度计算方法

Pearson 系数（Pearson Coefficient）


其中，

Pearson 系数的性质如下：

• 如果两条时间序列 ，则 表示它们是完全一致的，如果两条时间序列 ，则 表示它们之间是负相关的。
  
• 
  

可以基于 Pearson 系数来制定两条时间序列之间的距离：


其中
The First Order Temporal Correlation Coefficient

这个相关性系数与 Pearson 系数类似，但是略有不同，其定义为：

的性质：

• 
  
• 表示两条时间序列持有类似的趋势， 它们会同时上涨或者下跌，并且涨幅或者跌幅也是类似的。
  
• 表示两条时间序列的上涨和下跌趋势恰好相反。
  
• 表示两条时间序列在单调性方面没有相关性。
  

基于 CORT，同样可以定义时间序列的距离，用公式描述如下：

其中， 可以用 来计算，而
是一个递减函数。
基于自相关系数的距离（Autocorrelation-based distance)

假设时间序列是 ，对于任意的 ，可以定义自相关系数为：

其中 分别表示该时间序列的均值和方差。该公式相当于是比较整个时间序列 的两个子序列的相似度（Pearson 系数），这两个子序列分别是 和 。
于是，通过给定一个正整数 ，可以对每一个时间序列得到一组自相关系数的向量，用公式描述如下：


对于 的情况，可以假定 和 。于是，可以定义时间序列之间的距离如下：

其中的 表示一个 的矩阵。它有着很多种选择，例如：
（1） 表示单位矩阵。用公式表示就是

（2） 表示一个 的对角矩阵，其中 。此时相当于一个带权重的求和公式。

除了自相关系数（Autocorrelation Coefficients）之外，也可以考虑偏自相关系数（Partial Autocorrelation Coefficients），使用 PACFs 来取代 ACFs。这样，使用同样的定义方式就可以得到 和 两个距离公式。
基于周期性的相似度计算方法

这里会介绍基于周期图表（Periodogram-based）的距离计算方法。其大体思想就是通过 Fourier 变换得到一组参数，然后通过这组参数来反映原始的两个时间序列时间的距离。用数学公式来描述就是：


其中 ， ， 。这里的 表示 Gauss 取整函数。
（1）用原始的特征来表示距离：

（2）用正则化之后的特征来描述就是：

其中 ， ， 和 表示 的标准差（sample variance）。
（3）用取对数之后的特征表示：

基于模型的相似度计算

Piccolo 距离

基于模型的相似度判断本质上是用一个模型和相应的一组参数去拟合某条时间序列，然后得到最优的一组参数，计算两个时间序列所得到的最优参数的欧几里德距离即可。
模型有自己的 AR 表示，因此可以得到相应的一组参数 ，所以，对于每一条时间序列，都可以用一组最优的参数去逼近。如果


分别表示 和 对于时间序列 和 的参数估计，则 Piccolo 距离如下：

其中 ， 当 ，并且 当 。 当 ，并且 当 。
Maharaj 距离

按照之前的描述，可以增加一个矩阵来修改 Piccolo 距离：

其中 和 表示 模型对于 和 的参数估计，和 Piccolo 距离一样。 ， 和 表示时间序列的方差， 和 表示时间序列的 sample covariance 矩阵。
基于 Cepstral 的距离

考虑时间序列 满足 的结构，i.e. ，这里的 表示 AR 模型的参数， 表示白噪声（均值为 0，方差为 1 的 Gauss 正态分布）。于是可以从这些参数定义 LPC 系数如下：

当
当
所以，LPC 的距离定义是：

总结

在本文中，介绍了时间序列之间距离的计算方法，包括基于 范数的距离，基于相关性的距离，基于周期图表的计算方法，基于模型的计算方法。

长长的路

• 之前做过一个对time series进行burst prediction的项目，比较相关. 衡量的方法主要是DTW Distance和LB Keogh Distance.
  
• 至于如何更好地为两段或多段时间序列抽取feature，我主要用了两个feature，一个是feature_polynominal_coefficient，另一个是feature_symbolic_sequences. 其他的feature可能也会有一些帮助，比如z_normalization, mean, std_value, max_value, mean_value, idx_max, etc.
  
• 更多feature细节，可以参考下述论文的Time Series Features Section.
  
• Reference: https://arxiv.org/pdf/1401.2018.pdf
  

大力水手

可以了解一下shape based distance. 这种距离能很好地识别时间序列之间的trend的差别。详情可以参考Paparrizos和Gravano的paper: k-Shape: Efficient and Accurate Clustering of Time Series.

继续前进

好问题，我抛砖引玉吧
关于这个问题，私以为有篇文章总结的很好

2.1. Euclidean distance
2.2. Fourier coefficients
2.3. Auto-regressive models
2.4. Dynamic time warping
2.5. Edit distance on real sequences
2.6. Time-warped edit distance
2.7. Minimum jump costs dissimilarity

论文实验结果表明，这么多种距离，其实效果还是DTW和TWED最好哈哈
Ref：An empirical evaluation of similarity measures for time series classification