登陆有奖并可浏览互动!
您需要 登录 才可以下载或查看,没有账号?立即注册


×
方向导数和梯度概念辨析
我们在学习多元函数的时候,经常会困惑于方向导数和梯度的区别以及他们的几何意义,今天让我们来一起辨析一下。
一、什么是方向导数?
定义:函数的增量
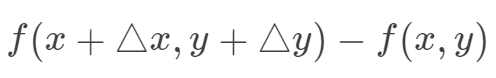
与
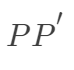
两点间的距离
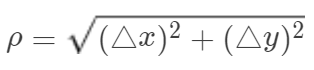
的比值,当
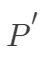
沿l趋近于P时,如果此比的极限存在,则称这极限为函数在P 点沿l的方向导数。记作
。
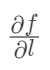
*也就是
。
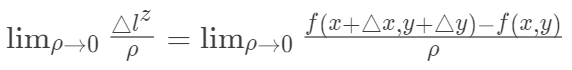
定义永远是晦涩的,如果我们来形象的类比一下,之前学到的偏导数是指当一个变量变化(例如:x、y),然后函数随着另一个固定变量的方向进行变化,偏导数就是变化的趋势。那么到这里的方向导数就是将偏导数的范围扩大化,从一个变量变化到两个变量甚至多个变量同时变化,但是这个变化同样是沿着空间中的一条线l。
我们来看方向导数的几何解释就会更直观的理解:

如图所示,图a指xoy平面内,曲线l的投影,我们所求的
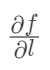
方向向量图b中就是p点上方z=f(x,y)曲线沿着曲线l切线的斜率,可以这么说:方向向量是你用一把名为切线的尺子在这个曲面上来回的摩擦,而这个方向向量就是你在各个l方向各个位置,这把切线尺子的斜率。
让我们在对照着图a,引出线面的定理:
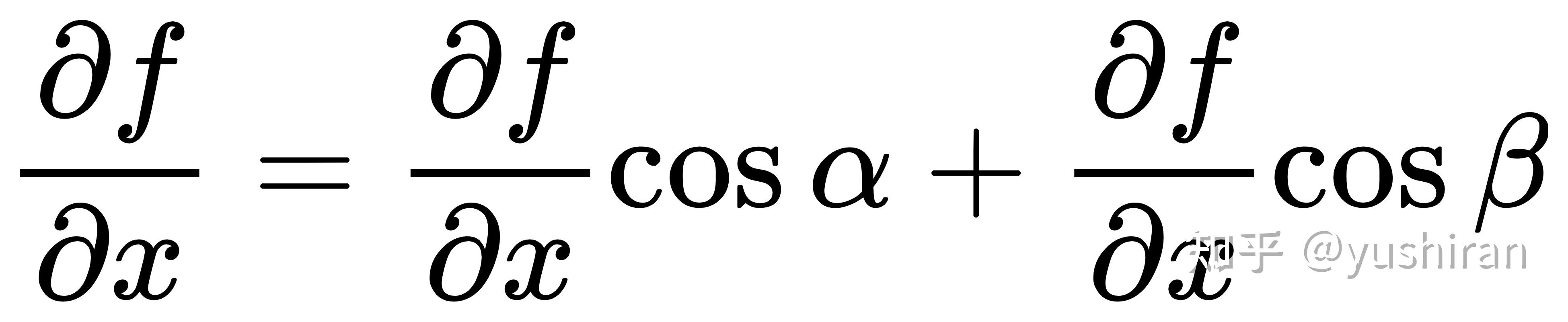
,其中
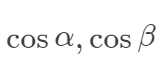
是方向l的方向余弦。
不难理解,其实方向向量可以用x和y两个方向的偏导数进行组合来表示,证明如下:
函数可微,那么等量可以表示为:
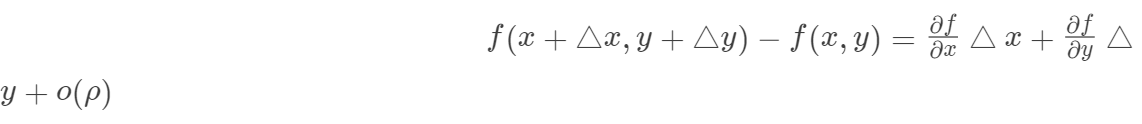
我们两边同时除以
,得
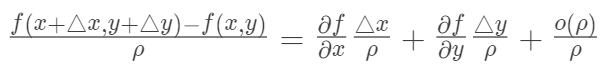
那么
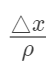
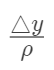
就是
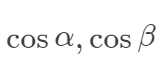
所以有
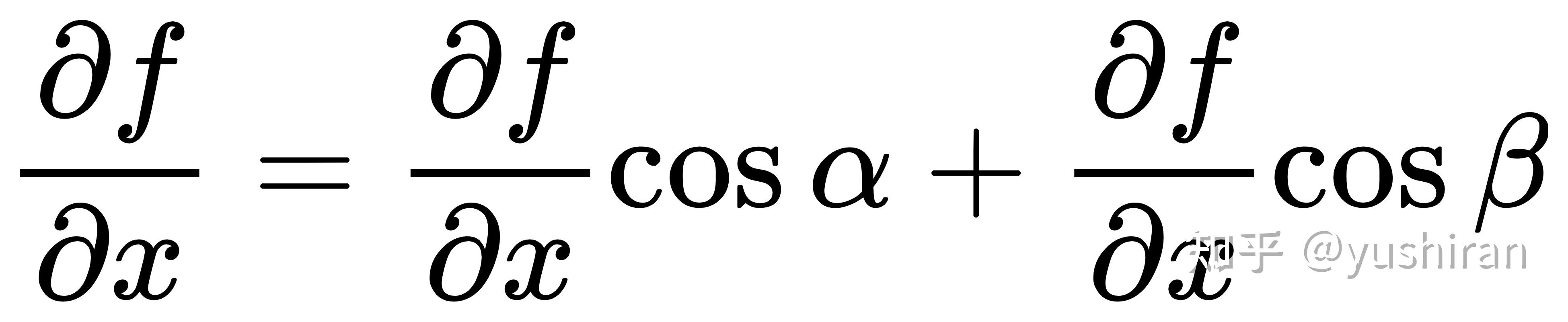
warning:
1、在这里我们要继续对偏导数和沿x、y轴的方向导数进行辨析:偏导存在是比沿x、y轴的方向导数存在更高级的概念,偏导存在能推出沿x、y轴的方向导数存在,反之不行。
2、以上概念都能推到多元函数。
二、什么是梯度?
定义:设函数z = f (x, y)在平面区域 D 内具有阶连续偏导数,则对于每一点

,都可以定出一个向量
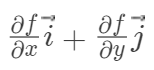
,这向量称为函数z=f(x,y)在点P(x,y)的梯度,记作
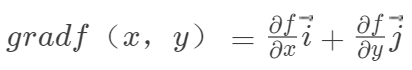
。
我们和方向向量进行比较,我们可以发现方向导数就是梯度乘以l方向上的单位向量。
可以这么说在梯度的方向上是方向向量取最大值的时刻,是函数值增加最快的时刻,如果用更形象的方法来比喻,
函数梯度方向和函数在这点等高线的发现的方向相同,且是从低等高线指向高等高线,而且模就是这个函数在这个法线方向的方向导数。
总结:函数在某点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为
方向导数的最大值.梯度的模为
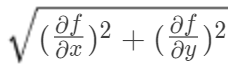
总结:
1、方向导数是数
2、梯度是向量
3、梯度的方向就是函数在这点增长最快的方向,以此类推,降低最快的就是梯度的反方向,变化最慢的就和梯度垂直。
最后,感谢你阅读完以上内容,你的赞是我继续记录的最大鼓励。
原文地址:https://zhuanlan.zhihu.com/p/360884968 |
 /3
/3 