金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
摘要
似乎所有人都知道时间的特殊性,但物理学——迄今最精密、最成功的科学怎么处理它?梳理2000多年来物理学的基本运动理论的发展,一个初步的脉络呈现在我们面前。亚里士多德认为时间维度与空间维度是互不影响的,空间维度可能更为重要——天上和地面的运动规律是不一样的。牛顿引入绝对时间与绝对空间的概念,在经典力学中时间维度是与空间维度地位平等的。牛顿提出三大运动定律以后,物理学的基本运动理论一分为三:爱因斯坦的(狭义)相对论力学、量子力学和演化力学。三个力学理论分别引入一个普适物理常数:真空中光速c、普朗克常数h和玻尔兹曼常数k,各自界定了对物理世界认识的一个极限:光速不变性、不确定性和不可逆性。对时间的认识也一分为三:量子力学基本沿用经典力学的时间概念;基于相对论力学时间与空间统一了,可以在一定程度相互转换,但基本的时序是相对性不变的,时间与空间有所不同;基于热力学第二定律和耗散-涨落定理所代表的不可逆性,演化力学给予了时间一个特别地位。这些显然还不是最后答案。三种普适力学若是统一,以后时间的作用怎样?
撰文 | 敖平(上海大学物理系、定量生命科学国际研究中心,上海交通大学系统生物医学研究院,现为四川大学教授)
从人类文明的曙光开始几乎所有人都知道、或觉得知道时间是什么,都感觉到时间在不停地流逝,过去、现在和未来是不同的。从古至今一直有人幻想能回到过去或知道未来,如各种穿越剧所演示。还有不少人想方设法让时间流动变缓、甚至停滞下来,众所周知的埃及法老企图用木乃伊来实现永生、秦始皇寻求长生不老之术就是这种不太成功的努力。人类对自然知识的积累到一定水平后开始理性地解释世界,试图了解时间这一现象的本质是什么和如何被描述,产生了各式各样系统的理论猜测和玄思。有起源于近东的宇宙有始有终的线性型体系;有印度的周期、轮回;也有我国《易经》里的不停变化。现存系统、努力去接近经验观察的体系由希腊亚里士多德提出并总结在他的《物理学》和《天论》两部著作中(图1)。这个古希腊知识体系强调逻辑的一致性,追求现象背后的动因和本质,明确认定时间的独立地位,同时也认为天空上星体的运动与地面附近物体的运动是截然不同的。这是物理学中的运动规律明确表达的开始,垂范学术界近2000年[1]。
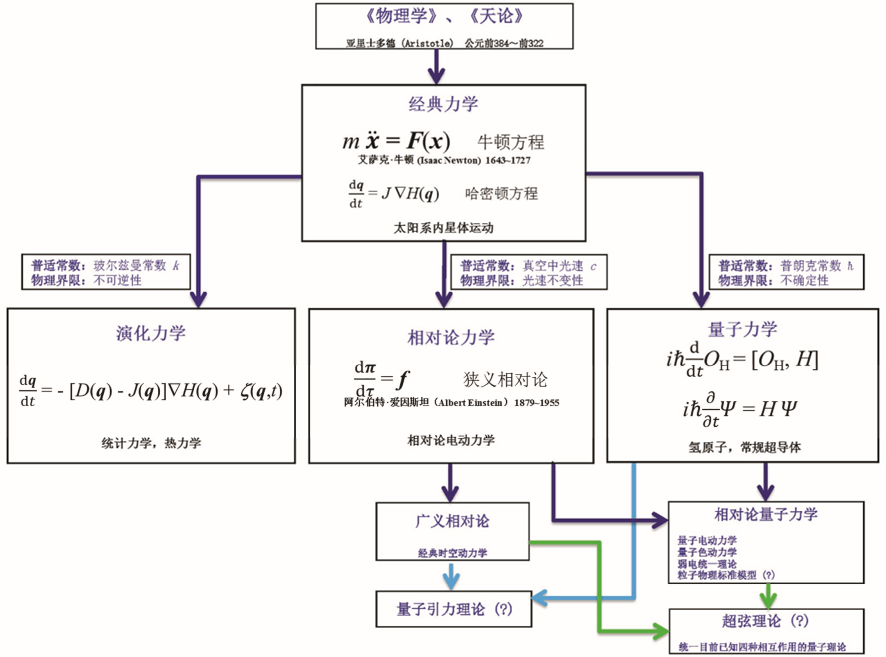
图1
01 牛顿的绝对时间
经过2000年左右的探索,人类逐渐认识到亚里士多德体系的不足,首先有对时间概念上的持续困惑。如对亚里士多德研究很深的著名宗教学者圣·奥古斯汀(St Augustine)很早就说道,“什么是时间?如果没人问我,我很清楚;如果有人希望我解释,我则不清楚”。亚里士多德运动规律与实验的偏差也积累到一个不可调和的程度,传说中的伽利略(Galileo)比萨斜塔实验非常有效和形象地说明当时的流行理论与实验的不符合。在总结前人的研究成果和他自己的实验、理论研究的基础上,牛顿在1687年系统地提出了著名的三大运动定律:
第一定律:每个物体如果没有外界影响使其改变状态,那么该物体仍保持其原来静止的或等速直线运动的状态;
第二定律:动量的变化与所施加的力成正比,并沿力的作用方向发生;
第三定律:对于每一个作用力,总存在一个与之相等的反作用力和它对抗。
三大定律与牛顿发现的万有引力定律一起实现了对天空中星体和地面上物体运动认识的统一[2],也让人类第一次有了对自然规律的定量、精密的描述,成为经典力学的基础。
为了更好地描述运动,牛顿发明了微积分(我怀疑可能是好的工具帮助他发现了新的运动规律)。不过由于这个数学方法太新,牛顿在他的书中仍然用古老但传统的数学方式——几何来表述三大运动定律,这导致我们现在阅读这部巨著的困难。我们现在常用的牛顿方程表述F=ma是牛顿提出三大运动定律50年后由伯努利(Bernoulli D)给出(图1),加速度a由牛顿记号表示,
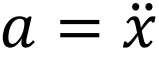
,物体位置x对时间t的二阶导数。牛顿方程在不同的问题中取同一形式——在经典力学中能应用于所有问题,但其中的力F和物体的质量必须由具体考虑的问题确定,如伯努利把牛顿方程从离散的有限粒子数系统推广到连续性的无穷粒子数系统,建立了流体力学。为了刻画物体位置,我们需要空间x,为了刻画运动,我们需要时间t这个维度。牛顿仔细地考虑了当时所有的实验结果,在逻辑一致性的要求下,他提出了绝对时间和绝对空间的概念。
牛顿第一定律界定了惯性参考系的存在,由于伽利略相对不变性的保证,时间的变化在所有惯性系中是一样的——时间的绝对性。惯性系需要的空间是欧几里德(Euclid)空间,甚至经过严谨、具有批判精神的哲学家之一康德(Kant)的分析,仍认为是先验地存在的。时间和空间在经典力学中是相互分离的,是两个不同的物理量或维度,但作为坐标具有一种平等的地位。
应用万有引力定律牛顿初步解决潮汐(月球和太阳的引力所导致)这一2000年难题,伯努利在1740年进一步发展平衡潮理论,结合牛顿方程,拉普拉斯(Laplace)在1776年提出动力潮理论,完整地解释了潮汐;哈雷(Halley)预测了一个慧星的运动周期——哈雷彗星在1758年如期归来;科学家们预测了新的行星的存在,海王星在1846年被观察到。经典力学取得了巨大的、前所未有的成功,它成为了科学理论的一个范本,影响远逾物理学的范围。
经典力学清楚地表明定量描述一个物理现象需要3个基本要素:运动方程——牛顿方程;物体本构方程——确定质量和力;初始和边界条件。运动方程和初始条件与时间关联,而力或相互作用的陈述和边界条件需要空间。物体在时空中的行为是可确定的。经典力学的成功给我们提供了一个普适物理理论的例子:能描述非常广泛的实验和经验事实、没有确定已知的实验反例、没有可预见的应用边界。经典力学有很多数学上等价表述形式,与我们论述相关的是著名的哈密顿(Hamilton)方程。它是关于物体在相空间q中的运动方程,用能量或哈密顿量H替代力 F的地位——相空间中H的梯度是广义的力(图1)。相空间q= (x, p) 由物体位置x和动量
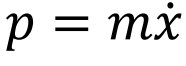
构成,图1中矩阵
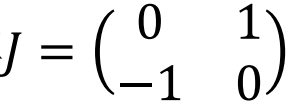
是对于x, p的反对称矩阵[3]。在哈密顿方程中,时间和空间的相对独立性被更清晰地体现。
但是,200年后经典力学在解释实验上开始出现困难,理论中隐含的矛盾逐渐明显。
02 相对论力学中的时间
第一个成功的突破口就是在绝对时间和空间这对概念。爱因斯坦长时间地思考了麦克斯韦(Maxwell)方程中伽利略相对不变性的不成立这个理论不一致问题,认为应该修改经典力学的相对性概念——扬弃伽利略相对不变性中时空的绝对性。1905年,爱因斯坦[4]提出了两条简洁的原理,相对性原理和光速不变原理:
(1)凡是对力学方程适用的一切惯性坐标系,对于电动力学和光学的定律也一样适用;
(2)光在真空中的速度c同发射体的运动状态无关.
这两条原理构成狭义相对论的理论基础,带来一系列观念的革命性变化。变化之一是同时性的可操作性建立,在不同的惯性系中不再有同一的同时性,时间的流逝在不同的惯性系中会是不一样的,狭义相对论和经典力学的时间同时性的不同,被著名的双生子佯谬形象地揭示。另一个直接的推论是时间维度、空间维度不再是相互独立,它们可以相互转化,一起构成四维时空,经典力学的绝对时空理论上不再成立。
重新定义相对性不变的四维力f和四维动量π,用固有时间或原时τ表示时间,力学运动方程仍具有同样简洁、优美的形式(图1),能与麦克斯韦方程完美地一致结合。相对论力学还预测能量和质量不再相互独立,可以相互转化——爱因斯坦著名的质能关系E=mc2。当然,在低速极限下,相对论力学回归经典力学。
100多年过去了,(狭义)相对论力学通过了迄今为止能做的、针对它的实验的检验,它的应用也给我们日常生活带来巨大影响。它已替代牛顿方程成为一个普适运动方程,是现代物理学的基础之一。1915年,爱因斯坦再次推广相对性原理为广义相对性原理,把万有引力也纳入相对论力学的框架中,进一步发展对时空的理论,再次增进了我们对时空的理解。他用黎曼(Riemann)几何替代欧几里德几何,用弯曲的时空替代平直的时空。我们所处的时空不单不是绝对或先验的,还依赖于其中的物质运动,时空可能会有起点。
从认识论的角度,黎曼空间的存在和应用也提示我们欧几里德空间不是哲学意义下先验的,广义相对论再次促成了对整个时间、空间观念的变革。从物理学本身发展的角度,相对论力学这个发展的例子告诉我们一个成功的新物理理论需要具备3个基本条件:包括旧理论的适用范围;预测新实验并通过其检验;有孕育新思想、新概念的能力。另一个众所周知的例子是经典力学:作为稳态极限,它成功地吸收了静力学如著名的阿基米德(Archimedes)浮力定律并具备上面讨论过的其他两个基本条件。
尽管相对论力学把时间、空间结合在一起,四维时空给我们时间维度、空间维度等价的想象,但它们之间的变换不像空间维度之间的变换那样任意。类时、类空和类光的四维时空是相对性不变的,我们不能把类时变换为类空。四维时空中发生的事件仍然有一个基本时序。时间维度与空间维度仍然不一样。
03 量子力学中的时间
第二个成功的突破口的成果是量子力学[5]。量子力学基本上还是沿用经典力学的时间概念,但从一个完全不同的角度变革了我们关于空间的概念:描述物体运动的相空间是有结构的。简单的例子是相空间中的位置x和动量p满足一个对易关系,[x, p]=ih,不再相互独立,它们的乘积不能交换,xp≠px。这个对易关系也是一对共轭物理量之间不确定性关系的典型例子。从1900年普朗克(Planck)发现普适常数到1925年海森堡(Heisenberg)发现第一个量子力学的表述花了至少两代物理学家四分之一世纪的时间。海森堡方程用算符OH表示物理量,直接用了对易关系(图1)。1926年建立的薛定谔(Schrödinger)方程也是常用的表述,用波函数ψ描述物体的时空状态,把相空间结构和对易关系隐含在其中。这两种描述绘景都需要首先确定系统的哈密顿量。在普朗克常数很小的条件下,量子力学回归到经典力学。
量子力学立即在从玻尔(Bohr)开始氢原子的理论研究中取得成功。一个非常成功的应用例子是超导现象:在我们熟知的一些科学家如费曼(Feynman)、朗道(Landau)等没有取得成功的情况下,一个由教授、博士后、研究生组成的理想的研究团队——但直到今天在专家范围外仍然不知名的团队在1957年发现了巴丁-库珀-施里弗(Bardeen-Cooper-Schrieffer)常规超导理论(巴丁是迄今为止唯一得过两次诺贝尔物理学奖的科学家)。这是一个非常深刻的理论,影响到物理学很多领域的发展,包括基本粒子物理的希格斯(Higgs)机制。与相对论力学一样,量子力学是现代物理学的基础之一,也对我们的日常生活有巨大影响,这是替代经典力学的第二个普适理论。
量子力学对时间、空间还各有一点重要突破。除了指明相空间有结构之外,量子力学明确表明描述物体运动的相空间不限于我们常见的三维空间(相空间是六维),别的维度也一定存在,别的空间方式也可用——恰当的一般空间是希尔伯特空间,完全脱离经典力学的相空间。例如基本粒子如电子的自旋,必须作为独立的、额外的自由度接受下来,这对后续量子场论的发展影响巨大。在时间上,量子力学表明一定程度的逆时间运动是可能的,从它的路径积分表述来看尤其明显:逆时间路径没有被排除,它的物理后果迄今还没有被探索清楚。量子力学与相对论力学相结合的狄拉克(Dirac)方程获得瞬时的成功。经过各自多年的几番努力,电磁相互作用、强相互作用、弱电相互作用的相对论量子场论化也获得成功。粒子物理的标准模型,统一电磁、弱和强相互作用的理论,也获得一定成功。这些成功理论的数学结构都属于杨振宁、米尔斯(Mills)所发现的规范场。但是,万有引力或广义相对论的量子化,还没有成功,有很强的理论矛盾;从量子场论的角度来包括广义相对论,如超弦理论,也还没有成功,还没有一个新的实验验证,它们在图1中用问号标识。在一定意义下我们又回到1905年之前的状态:各个理论之间还不完全融洽。这表明存在很深刻的理论问题,关键很可能是时间与空间在相对论中和在别的一般物理理论如量子力学中到底有何差别,有待我们继续探索。
04 演化力学中的时间
尽管它们的物理内容和数学结构完全不一样,量子力学与相对论力学的运动方程都有一个从经典力学带过来的共同性质:对于时间反演动力学是可逆的,孤立系统的能量是守恒的,信息或熵也是守恒的。有时人们会被自己手中的问题误导,会忘掉这个重要性质,譬如霍金(Hawking)就曾经忽视它而输了关于黑洞的宇宙信息守恒的赌,现在他认为黑洞是会带量子“软毛”的,会保留信息[6]。但是,过度强调这个守恒性质可能会导致另一个极端,把时间从物理规律的表述中取消,没有时间这个维度,从而把时间的存在看成是一种幻象[7]。这也是可以理解的:如果把能量看成“天”,把信息或熵看成“道”,我们已知两种普适动力学对于孤立系统无非是说“天不变、道也不变”。我们好奇的是,经典力学以后是否还有别的、不守恒的、第3种普适力学结构的可能?
事实上,19世纪中叶出现的热力学首先对这个问题提供了肯定回答的可能。早于相对论力学和量子力学的发展,热力学第二定律[8]明确陈述一般动力学过程是不可逆的,它是人类发现的普适规律之一,迄今没有任何实验、经验上的例外。但是,热力学不是真正的动力学,这让它催生了两个重要问题:它的存在与已知的普适运动规律相容吗?如果相应新的运动方程存在的话,一般形式会是什么?
从麦克斯韦、玻尔兹曼(Boltzmann)、吉布斯(Gibbs)等开始的150多年研究对第一个问题给出了肯定回答:相容;并产生了一门对应的、应用范围与热力学一样广泛和成功的学科——统计力学[9],是现代物理学的一块重要基石。对第二个问题的回答有两个相反的努力方向:不可逆性仍然由可逆的运动规律中产生;或寻找全新的结构。从玻尔兹曼开始的物理学主流希望不可逆性能够从已知的运动规律产生:经典力学和量子力学。很遗憾,这种努力经过150多年还没有成功:常见的问题是明确地或隐蔽地总是把不可逆性的假设引入到论证过程中。其余的研究要么论证过程有错、要么系统太特殊。但这个探索带来了很多重要成果,加深了我们对运动规律的理解,例如混沌的发现与研究[10]。
第二个方向把研究者们带到全新的领域,遇到的不可逆的运动方程太多了,可用的方法真是“八仙过海,各显神通”,一般的意见对能否得到肯定的答案一直是不确定的。譬如直到最近(甚至现在)很多人对一般非平衡过程中是否存在类似的能量函数H、统计力学是否存在一个普适的力学框架仍然持一个怀疑态度[11]。幸运的是,第一个对应于统计力学或热力学的一般运动方程终于出现了,它的形式也非常“简单”(图1)。
这个演化方程[12]很新,我国物理学家对它的建立有主要贡献。首先,与另外的基本力学理论类似,方程的形式是理论假设,演算结果是可以被实验检验的。演化方程是在相空间q中表述的,ζ是相空间中的随机“力”,是高斯白噪声,它的平均值是零,〈ζ〉=0,
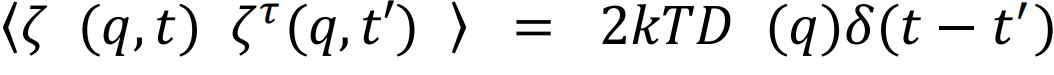
,其中:k是玻尔兹曼常数,T是温度,上标τ表示转置,δ(t)是狄拉克δ函数,D是相空间中的扩散矩阵。J(q)是一个一般的反对称矩阵。如果稳态极限存在,其分布函数是标准的玻尔兹曼-吉布斯分布形式,
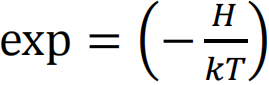
,是统计力学中重要的正则分布。
这个演化方程显然满足成功的新物理理论所需要具备的3个基本条件之一——包容旧理论的适用范围。当D=0,它回到经典力学——孤立系统运动的哈密顿方程;它直接导出统计力学的正则分布,不需要通常教科书中的大粒子数条件[13];也与从完全不同视角得到的运动方程一致[14]。另一个基本条件也满足——孕育了新思想、新概念:它统一平衡态和非平衡态过程的描述;指出存在一种全新的不同于常见伊藤(Ito)和斯卓妥诺维奇(Stratonovich)积分的随机积分[15],对应的随机微分方程自发现以来不停地在被研究[16-19]。从演化力学用极限(D=0)包容经典力学的例子中看到,随机力的起源是系统的开放性:系统之外的、别的自由度存在,它们的影响导致随机力,一般来说随机力含有系统力学量或相空间的变量,具体形式必须由具体问题决定。演化方程的很多特殊例子已经被很多研究者发现[14],但对其隐含的普适性认识不足,目前为止的主流认为应该从守恒的运动方程导出,忽视了这种推导需要一组全新的额外假设[13]。
随机“力”ζ与扩散矩阵D的关系是统计物理中著名的耗散-涨落关系的一个特例,但在演化力学的表述中是作为定义出现的,可称为“F定理”,这意味着它在演化力学中普遍成立,实验上是可以检验的。这个定义可以看成牛顿第三定律的一个推广:物理体系如何与未知的世界相互作用。更进一步的研究发现系统的扩散矩阵和摩擦矩阵还应该满足一个普适的关系[12],爱因斯坦关系——摩擦系数与扩散系数乘积是常数——在高维、非线性、无细致平衡情况下的推广,是一个新的预测,也能被实验检验。
演化力学预测了一系列随机动力学等式,其中一部分是熟知的热力学不等式的推广,可由实验检验[12]。它也指出目前基于平均场意义下的热力学第二定律会在涨落大的情况下出现与实验的偏差,应该重新检验其陈述。演化方程所依赖的新的随机积分[14]在物理系统中也是可以检验的,意义类似于广义相对论中空间是否弯曲。成功的新物理理论所需要具备的3个基本条件演化力学都能满足。数学上,演化力学是基于新发现的一个强有力的数学结构[16, 19]:一个随机过程中总存在一个类似于物理中能量的函数,记为H,动力学过程可以分解为两部分:保持H不变的部分,记为J让H减少的部分,记为D,由随机项的方差确定。演化力学可以作为第3个普适力学,是现代物理学的另一基础。
演化力学提供了描述非平衡态过程的一般框架,它的稳态极限——统计力学是目前应用广范、成功的物理理论[20]。不但成功地运用在宏观世界,而且也成功地运用在量子场论描述的微观世界和广义相对论表述的宇观世界。演化力学以一种完全不同于量子力学的方式引入不确定性,假设物理体系是开放的、实际过程总是不可逆的。在量子力学中不确定性是关于相空间或共轭物理量的,而运动过程是可逆的。演化力学中的可逆性类似于科学的重要基石之一——测量,测量过程是不可逆的。在经典力学中测量对系统的影响在理论上可以无限地小以至于能被忽略不计,而在量子力学中测量有小单位,~hIn2,普朗克常数和比特。从这个角度演化力学会对解决量子力学中的测量问题——玻尔和爱因斯坦终生讨论但没有获得共识的问题提供一个重新考虑的思路。
与量子力学一样,演化力学基本沿用经典力学的时间概念,在惯性系之间不做区别,对空间的要求也与量子力学一样,可以是任意空间。这让它甚至能应用到物理学的范围以外,事实上它的发现就受到生物学中达尔文(Darwin)演化过程的启发[12]——玻尔兹曼就曾经这样猜测过,但他卡在怎样处理无细致平衡的运动。它与量子力学和相对论力学(包括经典力学)大的不同是:在演化力学中能量和信息都不守恒了,把不可逆性显式地容纳在内,明确揭示时间维度和空间维度的不一样。
05展望
从运动规律的发展历程中我们看到时间维度是如何与其他维度不一样的。目前我们所知的3种普适力学各有一个普适常数:c,h和k,分别揭示了物理世界的一个认识界限:光速不变性、不确定性和不可逆性(图1)。其中,两个界限与时间相关,在一定程度上物理学已回答了时间为何不同于其他维度。更完整的回答可能涉及对一个客观世界的根本规则——因果关系的更深刻理解,也许要等到对3种普适力学有更进一步理解之后。
此外还有一系列的与时间相关的问题需要回答,难度也许要小一点:我们注意到相对论量子场论是相对论力学与量子力学的优美结合,但它连接到演化力学或统计力学就显得特设性很强,目前好的做法之一是久保-马丁-施温格(Kubo-Martin-Schwinger)条件,在理论上还可以比这个条件做得更好吗?超弦理论中的多宇宙理论已经在应用演化理论,后者的角色可以更大吗?我们能把3种普适力学都统一在一个理论构架中吗?这个统一是会在统一四种相互作用之前还是之后?我们的宇宙到底是孤立的还是开放的?等等。对有志探索的人们,也许第一步是了解物理学已经取得的、比较确定的成就[21]。然后,体验、享受你的探索历程。或者,纯粹来欣赏人类理解时间这一艰苦卓绝的奋斗。
参考文献
[1] Aristotle. Complete Works of Aristotle (v1). New York: Princeton University Press, 1984
[2] Newton I. The Principia: Mathematical Principles of Natural Philosophy. New York: University of California Press, 1999 [Newton I. 赵振江, 译. 自然哲学的数学原理. 北京: 商务印书馆, 2006]
[3] Peng H W, Xu X S. Introduction to Theoretical Physics (in Chinese). Beijing: Peking University Press, 1998 [彭桓武, 徐锡申. 理论物理基础. 北京: 北京大学出版社, 1998]
[4] Zhang Y Z. Experimental Foundation of Special Relativity (in Chinese). Beijing: Science Press, 1979 [张元仲. 狭义相对论实验基础. 北京: 科学出版社, 1979][5] Wang Z X. Principle of Quantum Mechanics (in Chinese). 2nd ed.. Beijing: Peking University Press, 2008 [王正行. 量子力学原理. 第 2 版. 北京: 北京大学出版社, 2008]
[6] Hawking J W, Perry M J, Strominger A. Black holes have soft quantum hair. Phys Rev Lett, 2016, 116: 231301
[7] Barbour J. The End of Time. New York: Oxford University Press, 2000
[8] Wang Z X. Thermodynamics (in Chinese). 2nd ed. Beijing: Peking University Press, 2014 [王竹溪. 热力学. 第 2 版. 北京: 北京大学出版社, 2014]
[9] Gibbs J W. Elementary Principles in Statistical Mechanics. New York: Charles Scribner’s Sons, 1902 [Gibbs J W. 毛俊雯, 译. 统计力学的基本原理. 合肥: 中国科学技术大学出版社, 2016]
[10] Hao B L. Directions in Chaos (1&2). Singapore: World Scientific, 1987, 1988
[11] Lu X Y, Lin J Z. Can we develop a general theory of the dynamics of turbulent flows and the motion of granular materials (in Chinese)? Chin Sci Bull, 2017, 62: 1115–1118 [陆夕云, 林建忠. 能否发展关于湍流动力学和颗粒材料运动学的综合理论? 科学通报, 2017, 62: 1115–1118]
[12] Ao P. Emerging of stochastic dynamical equalities and steady state thermodynamics from Darwinian dynamics. Commun Theor Phys, 2008, 49: 1073–1090
[13] Ao P. From N=∞ to N=1: Arrival of dynamical foundation for statistical mechanics (in Chinese). In: TD Lee Library, ed. Essays in Honor of the 90th Birthday of TD Lee. Shanghai: Shanghai Jiao Tong University Press, 2016. 281–287 [敖平. 从 N=∞到 N=1: 期望已久的统计力学普适动力学基础已到来. 李政道图书馆, 编. 心通天宇——李政道教授九十华诞文集. 上海: 上海交通大学出版社, 2016. 281–287]
[14] Ao P, Kwon C, Qian H. On the existence of potential landscape in the evolution of complex systems. Complexity, 2007, 12: 19–27
[15] Qian H, Ao P, Tu Y, et al. A framework towards understanding mesoscopic phenomena: Emergent unpredictability, symmetry breaking and dynamics across scales. Chem Phys Lett, 2016, 665: 153–161
[16] Ao P. Potential in stochastic differential equations: Novel construction. J Phys A, 2004, 37: L25–L30
[17] Kwon C, Ao P, Thouless D J. Structure of stochastic dynamics near fixed points. Proc Natl Acad Sci USA, 2005, 102: 13029–13033
[18] Ma Y A, Tan Q J, Yuan R S, et al. Potential function in a continuous dissipative chaotic system: Decomposition scheme and role of strange attractor. Int J Bifurc Chaos, 2014, 24: 1450015
[19] Yuan R, Tang Y, Ao P. SDE decomposition and A-type stochastic interpretation in nonequilibrium processes. Front Phys, 2017, 12: 120201
[20] Ao P. The work of David J Thouless: The discovery of topological phase transition led by curiosity (in Chinese). Chin Sci Bull, 2017, 62: 1199–1203 [敖平. 大卫 邵勒斯的治学和建树: 纯粹探索凌绝顶. 科学通报, 2017, 62: 1199–1203]
[21] Brown L M, Pais A, Pippard B. Twentieth Century Physics (I-III). New York: CRC Press, 1995 [Brown L M, Pais A, Pippard B. 刘寄星, 译. 二十世纪物理学(1–3). 北京: 科学出版社, 2014]
本文原文发表于《科学通报》2018年第2期,经作者授权发表于《返朴》。 |
|
 /3
/3 