使用Probit法探寻核酸检测的边界与底线

二、Probit 方法计算LOD的实验要求

1. 最小实验设计

针对每个待评估的测量程序，建议的最小样本量和配置如下：

2. 关键：稀释液的分布要求

    稀释梯度的设计直接决定了 Probit 回归的拟合质量。如果所有数据点都是 100% 或 0% 检出，模型将无法收敛。因此要求：

• 中间区间：至少有 3 个 稀释度的阳性率落在 0.10 到 0.90 之间（即 10%-90% 阳性率）。

• 高位区间：至少有 1 个 稀释度的阳性率 > 0.95（确保包含 LoD 附近的点）。

  

3. 基因型与亚型

如果被测物（如病毒、细菌）存在遗传变异，实验设计应纳入所有主要基因型的代表性样本，确保 LoD 覆盖临床常见的亚型。

4. 数据分析步骤

汇总数据：计算每个浓度点的阳性率。

模型拟合：使用统计软件（如 SAS, JMP, R, Minitab 等）进行 Probit 回归。

质量检验：使用 Pearson 卡方检验评估拟合优度。如果拟合不佳（p < 0.05），可能需要增加稀释点或重复次数。

计算 LoD：从模型中推导出 95% 概率对应的浓度值。

最终定值：如果评估了多个试剂批次，应取各批次 LoD 计算值的最大值作为该产品的最终 LoD。

三、 Probit 方法计算原理与公式

    Probit 方法是一种统计回归分析技术，核心在于将非线性的“浓度-概率”关系转化为线性的数学模型。主要用于评估分子测量程序（如核酸检测或传染病检测）的检测限 (LoD)，这些程序的检测能力以阳性率（即阳性结果数与重复测试总数之比，也称为 Hit Rate）来衡量,。

1. 阳性率（Hit Rate）计算

对于第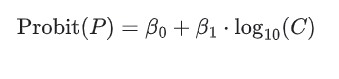 

• Probit(P)：阳性率对应的标准正态分布分位数。可以查标准正态分布分位数表。或者利用 Excel 函数将阳性率（P）转换为标准正态分布的分位数（即 Probit 值）Y = NORM.S.INV(P)
  

  例如，95% 的阳性率对应的 Probit 值约为 1.645 。

  注意：如果阳性率为 0% 或 100%，该函数会报错（返回无限大）。实际操作中，通常将 0% 修正为 1/2N，将 100% 修正为 1 - 1/2N，其中 N是重复次数。

• C：分析物浓度（通常取 log10 以改善拟合效果）。

• β0，β1 ：通过最大似然估计法（MLE）计算出的回归系数。

• β0：为拟合直线的截距（ Intercept），β0=Intercept（Y值集合，X值集合）
  

• β1：为拟合直线的斜率 （Slope），β1=slope（Y值集合，X值集合）

  
  3. LoD 的计算

  当设定目标阳性概率为 95% 时（即β= 0.05），将对应的 Probit 值（1.645）代入方程反解出浓度 C：

  

  

• 四、 实例解析：流感病毒荧光定量 PCR (Flu qPCR)
  

      在 CLSI EP17-A2 指南及 Probit 回归分析中，系数β0（截距）和 β1（斜率）的获取通常有两种途径：“专业统计软件法（最大似然估计 MLE）” 和 “Excel 简易估算法（线性回归近似）”。

  对于大多数实验室用户，如果没有 SPSS 或 SAS 等专业软件，可以使用 Excel 进行线性回归近似计算，虽然精度略逊于 MLE，但在 LoD 评估中通常是可以接受的。

1 实验数据收集

    我们制备了一系列已知浓度的流感病毒 RNA 标准品（单位：copies/mL），并对每个浓度进行了 20 次重复检测。数据如下：

2 数据分析步骤

Excel 计算演示（以流感 qPCR 为例）：

假设重复次数 N=20。

• X = log10(C)，Y=Probit 值

• 计算 β1：=斜率SLOPE(Y列, X列)≈ 2.78

• 计算 β0：=截距INTERCEPT(Y列, X列)≈ -2.53

    得到方程：Y =  2.78 X-2.53