分析测量范围即定量检测项目的线性检测范围,是整个检测系统(包括仪器、校准品、试剂、质控品、操作程序以及检测人员)对应于系列分析物浓度(活力)的仪器最终输出的信号间是否呈恒定比例的性能。
下面本篇从定义,及CLSI EP-6中分析测量范围的评价方案两方面来进行介绍。
分析测量范围:指患者样本未经任何处理(稀释、浓缩或其他预处理),由检测系统直接测量得到的可靠结果范围,在此范围内一系列不同样品分析物的测量值与其真实浓度(真值)呈线性比例关系。
临床可报告范围:指定量检测项目向临床能报告的检测范围,患者样本可经稀释、浓缩或其他预处理。
对于临床可报告范围大于分析测量范围的检测项目,需进行最大稀释度验证试验,并结合临床决定水平和功能灵敏度来共同确定该项目的临床可报告范围。
若临床可报告范围小于分析测量范围,则需进行最大浓缩度验证试验确定临床可报告范围。
线性范围:指覆盖检测系统的可接受线性关系的范围,非线性误差小于设定标准。当某分析物浓度或活性的测量值与真值呈数学上的直线关系时,则认为这种定量测定方法是线性的。
线性:检测样本时,在一定范围内可以直接按比例关系得出分析物含量的能力。
线性偏离:也称非线性程度,当某组数据被评价为非线性时,在某一浓度处最适二次(三次)多项式与一次多项式(线性)拟合模型的差值。
允许偏差/误差:在一个监测系统中,来自各种因素的,用户能够承受并能满足医学要求的分析偏差大小。通常单次检测的允许误差范围用样本测量的靶值±允许误差来表示。
回归标准误差:多次重复检测结果的均值和可接受参考值的一致性。
早在1986年CLSI就发布了EP6-P的建议性文件,但由于其采用单一直线回归处理,采用最小二乘法回归分析拟合最适直线,统计学方法为线性失拟误差,这种方法的缺点是易受检测方法的精密度影响。
如果精密度很好,在线性的表现上稍有非线性,统计就认为无线性,方法被否认;若精密度稍差,线性即使有问题,统计可能得出“线性”的结论,无法客观反映线性状况。
2003年新发布EP 6-A指南,文件中采用多项式回归作为分析现行的评价方法。该文件采用了二元一次直线回归、二次与三次的曲线回归统计处理,以统计估计值与实际检测值的差异(统计误差)来判断,统计误差最小的为最适合直线或曲线。
而且在分析过程中和临床应用紧密结合,设定临床允许偏差。但线性评价的结果从统计学上认为非线性,但是若采用线性方式处理患者结果,引入的误差不超过临床允许误差,可以接受作为先行处理,称为临床可接受限性,这与之前相比做了很大改善。
熟悉仪器设备:进行评价分析的操作人员必须十分熟悉仪器的操作,质量控制和校准方法,以及正确的收集样本。
实验时间:全部试验尽可能在较短时间内完成,如可能,单个分析实验最好在一天完成。
实验样本:
样本数量:5个测量点为最低要求,因为判断“S”形曲线至少需要5个点。
证明线性范围:5~7个样本;验证声明:7~9个样本;
建立线性范围:9~11个样本。每个样本重复2~4次。样本浓度差异可以不是等间距。
基质效应:
样品类型应与临床测试所用样品类型相似,且不含厂家所声称的干扰因素(溶血,黄疸,脂血等)。理想样本为患者样品。
当高浓度患者样品不易获得时,可通过在低浓度水平的患者样品中添加分析物的方法来制备所需浓度,但原则上加入分析物浓溶液的体积要少于总体积的10%。低浓度的样品可以从患者样品中获得,可以用来稀释高浓度样品,或与高浓度样品共同配制中间浓度水平的样品。
分析范围:
选择的分析范围应包括或等于厂家所声称的最低和最高浓度范围。其重要注意几个重要的浓度:最低分析浓度或线性范围的下限,不同的医学决定水平值,最高分析浓度或分析测量范围的上限。
样品准备和浓度计算:
分别准备高浓度样品(接近或位于线性范围上限,H)和低浓度样品(接近或位于线性范围下限,L),用两者配置成一系列浓度水平的待测样品(至少5个待测样品),每水平浓度计算公式为:
测量前,必须保证仪器的校准和质控状态。
测量顺序应该是随机的。
如果存在携带污染,则需在每个检测样品之间加入至少2份低值样品(L),且这2份低值样品检测结果,不纳入统计。
离群值检查:EP 6-A中,离群值是指检测结果不适用其它数据所拟合的模型,可以通过统计学方法计算,但在对线性区间评估时,可通过目视检查检测值与预期值就可以发现离群值。
需要注意的是这里的离群值是指单个检测结果,而不是只某个浓度水平的多次测量结果的均值。如果离群值≤1个,可以直接删除此离群值;如果离群值超过1个,则需重新评估检测系统的精密度。
确定分析测量范围:在此过程中需分两部分进行,第一步判断用非线性多项式拟合数据是否比线性好,以此确定是否用非线性拟合;
第二步是当非线性多项式拟合数据点优于线性拟合时,要判断最适非线性模型与线性拟合之间的差值是否小于预先设定的该方法的允许偏差。
一次多项式模型为直线,判断某种方法是否呈线性的方程;
二次多项式模型为抛物线反应曲线,b2为非线性系数。有增加或减少的趋势两种情况;
三次多项式模型为“S”形反应曲线,b2,b3为非线性系数。在测量范围内的两端呈非线性。
第一步确定过程:分别对测量数据进行,可依据统计学软件进行一次,二次,三次多项式拟合。并对二次,三次多项式模型,需要判断非线性系数是否具有统计学意义,即与0之间是否有无差异。统计学方法为t检验,
中SEi为截距b0的标准差;
为将各个X带入一次多项式拟合方程计算的值,
为实测均值与回归计算值的差值,n为总测量次数。
自由度为df=L·R-Rdf,L为不同浓度的样本数,R为重复检测次数,Rdf为回归分析时占用的自由度。如果t<t0.05,则认为非线性系数不显著,是线性回归;如果t≥t0.05,则认为非线性系数显著,是非线性回归。
第二步确定过程:
判断非线性程度是否小于预先设定的允许偏差。每个浓度处的线性偏离计算公式为DLi=p(xi)-(b0+bixi)。p(xi)为第一步所确定的最适多项式回归模型在xi处的值,二次或三次多项式和一次多项式的预期值及线性偏离结果进行分析。
其中DLi与该测量值浓度单位一致,如果要换算成百分比,则将每个DLi除以该浓度值(已知值)或测量均值(相对浓度)在乘100%。
为方便大家理解,下面举例说明。
比如验证某检测项目的线性,对6个不同稀释浓度的样品进行测试,每个样本按随机方式重复测定2次,在同一天内完成。分别作一次,二次,三次多项式回归,根据本篇中所介绍的公式可得出以下数据。








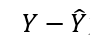


 /3
/3 





 浙公网安备33010802005999号
浙公网安备33010802005999号


