请问假设检验（hypothesis testing)的意义到底是什么，它的原理是什么样的？

病理医师

我明白具体的计算以及基本原理，题目什么的都会做了，但是不是很明白hypothesis testing 这个方法是如何发明出来了，有没有什么推导方法以及具体原理。题主是物理系小白，数学不好，可能太专业的数学语言会有点搞不明白…………

原文地址：https://www.zhihu.com/question/323210651

长长的路

假设检验简单来说，就是下面4步的推理逻辑：


为了你更容易理解，我还是从一个生活中的例子开始聊起。
这个例子里举王宝强和马蓉的例子并没有恶意，只是想说明假设检验的背后逻辑，而这个例子更容易让你理解清楚。

有一天，宝强怀疑妻子有可能出轨，但是自己逻辑能力太弱，于是就请了我这个侦探来帮他破案。
于是，我就拿出了自己的杀手锏武器，也就是破案的套路：假设检验。

第1步，我需要明确问题是什么。

问题：宝强要检验马蓉是否出轨
根据这个问题我提出来下面两个互为相反的假设。
零假设：马蓉没有出轨
备选假设：马蓉出轨了


为什么要提出两个假设呢？
因为从逻辑学来看，如果我们能够证明某个零假设不成立，那么其对立假设（也就是备选假设）肯定为真。
零假设和对立假设在逻辑方面是互补的，也就是说，如果其中一个假设为真，则另一个假设为假；如果我们推翻了其中一个假设，那就必须承认另一个假设。

对应这个例子里，如果我能找到足够强的证据来否定零假设（也就是马蓉没有出轨），那么我就能有效的说明零假设不成立，那么备选假设成立。

好了，接下来的问题就是：如何找到证据了。下面图片我们看下第2步

第2步：证据是什么？

根据中心极限定理，我们知道，合理足够多的样本可以代表总体。所以我要找到马蓉合理的样本数据来做证据。

接下来，我随机调查了马蓉这几年的样本数据，包括上网，开房，财务等。
根据这些样本数据显示出来的证据，我利用自己的统计概率知识，计算出了，在零假设成立的前提下，马蓉没有出轨的概率。


不算不知道，一算吓一跳。在零假设成立的前提下，样本数据计算出马蓉没有出轨的概率是0.01%

这个概率值在统计概率中有个专门的术语叫p值。也就是，在零假设成立的前提下，得到样本观察结果出现的概率。

在这里p值就是在零假设成立的前提下（马蓉没有出轨），用样本证据计算出的马蓉没有出轨的概率，p=0.01%

现在我们来看第3步：判断标准是什么

我不能说有了证据就立马说明人家马蓉出轨，错误的判断会造成宝强家庭的毁灭性破坏。
所以，提前制定好一个定罪的标准，有助于我能做到：绝不能冤枉一个好人，但也不可放过一个坏人。

因为我定的零假设是：马蓉没有出轨。所以这里定的标准是，如果马蓉没有出轨的概率<=5%，那么就直接否定了零假设，也就是马蓉没有出轨不成立。

这里比较拗口，马蓉没有出轨的概率<=5%，反面就是马蓉出轨的概率大于95%，所以马蓉有很大概率出轨，因此把零假设：马蓉没有出轨否定了。

这里用于做出决策的标准5%，在假设检验里叫做“显著水平”，用符号α：Significance Level (Alpha)表示，是一个概率值。

第4步：做出结论

那么，马蓉到底有没有出轨呢？

我们将样本证据计算出的p值与判断标准α比较下就可以了：
如果p< =α，那么拒绝零假设，也就是备选假设成立。
如果p>α，那么零假设成立

这代表什么意思呢？
α是判断标准，也就是小于这个值就表示零假设不成立。
p值在零假设成立前提下，用样本证据得出的概率，在这里表示有样本证据得出马蓉没有出轨的概率。

通过比较这两个值，我们发现：p远远小于α。

马蓉小姐姐，样本证据对你大大不利啊。本想零假设证明你没有出轨的，但是样本数据给出的证据，也就是你没有出轨的概率只有0.01%，这个概率远远小于判断标准5%

所以，我可以大胆的拒绝零假设。

回到我们一开始提出的假设：如果零假设不成立，那么预备假设成立。
现在样本数据显示零假设不成立，所以预备假设成立，也就是马蓉出轨了。

我将这个毫无破绽的推理过程告诉宝强后，宝强顺藤摸瓜发现名下财产也被马蓉卷跑。最后再考虑各种解决方法后，选择了求助于法律手段。并在微博上公布了这件事情，求助于舆论的压力。



福尔摩斯说：一旦排除所有的不可能，剩下的不管多么难以置信，一定就是真相。
在唐人街探案中，刘昊然和王宝强破案时，也引用了这句话

总结

最后，我们总结下假设检验的逻辑套路，你就更清楚了。


第1步：问题是什么？
确定你要研究的问题是什么。
根据这个问题我提出来下面两个互为相反的假设。
零假设：马蓉没有出轨
备选假设：马蓉出轨了

第2步：证据是什么？
在零假设成立的前提下，我们认为手头已有的数据是从零假设为真的总体中随机抽样得到的一个样本，但是这个可能性是多少？所以我们需要计算出这个概率，就是p值。
在例子中就，我们得出的证据显示，马蓉没有出轨的概率p=0.01%

第3步：判断标准是什么？
需要建立判断标准来检验证据是否有效。
假设检验常用的判断标准是与0.1%，1%，5%，在假设检验里叫做“显著水平”，用符号α，
它是一个概率值，用于表示不可能发生和可能发生的临界值。

第4步： 做出结论
根据你找到证据，和自己的标准，你做出了正确的结论。这是一种使用数据和概率来做决策的过程。

我们将样本证据计算出的p值与判断标准α比较下就可以了：
如果p< =α，那么零假设不成立，也就是预备假设成立。
也就是如果得到样本平均值的概率p值小于显著水平（5%或者1%或者0.1%），那么通常被视为不太可能发生，拒绝零假设。

在前面的例子中，p值是指在零假设成立前提下，用样本证据得出的概率，在这里表示有样本证据得出马蓉没有出轨的概率。

如果p>α，那么零假设成立

通过比较这两个值，我们发现：p远远小于α。
从而证明零假设不成立，备选假设成立，也就是马蓉出轨了。

假设检验这个过程，虽然套上了统计概率的外衣，但是说白了，底层思想其实很简单，就是：一种逻辑推理的套路。
这个逻辑推理，其实我们每天都在用。我们平常说某个人心思细腻，逻辑严谨。其实你也可以做到，那就是掌握今天的逻辑推理套路：假设检验。
参考资料：
他是如何用批判思维的工具：假设检验，改变自己命运的
假设检验更多的案例，以及如何使用Python进行假设检验的项目
<hr/>
数据分析入行指南：助你互联网行业发展有「钱」途

感恩由您

说实话，这个问题我曾经学hypothesis testing（HT）假设检验的时候也问过！
题主已经明白具体的基本原理，题目什么的都会做，现在开始思考背后的东西，这是一种个人非常认可的思考问题方式！

什么是假设检验？

无论是通俗易懂的表述还是technical的解释我相信已然一抓一大把了，这里就不赘述了。总而言之，这次的中文构成无非就是，"假设”和“检验”（当然英文其实也是如此）。
那什么是假设呢？顾名思义，假设就是我们对于数据所在“总体”的一些假定，比如其数据的概率分布， 比如说总体的一些统计特征，均值，方差等等， 又比如总体的趋势变化特征（ordinal的数据），上升下降，甚至严格单调上升下降，当然这里推广一下还有Rank的变化。
那为什么要有这些假设呢？
因为是想要对数据的总体趋势有一定的直观的了解，而且这种直观的了解可以被方便地量化验证！
这里就引出了假设检验的中的第二个关键词，“检验”！
那么什么是检验呢？顾名思义，检验就是我们根据已有的“样本”对已经被假设的内容进行确认的过程， 比如我们对数据总体的分布进行假设，而现在要通过已有数据的empirical分布来验证其是否大概率来自于一个我们已知特性的分布，比如是不是正态分布的呀！

假设检验如何是如何操作的呢？

Again，具体的操作tutorial实在太多了， 甚至总结都多的不能再多了，这里我就高度抽象的再总结一下.
之前说到我们对于假设检验，至少先要有假设，对吧？那有了假设之后现实无非就是两种情况：

• 假设成立
  
• 假设不成立
  

因而，其实更具体一步来说，无非是考虑，在关于总体的假设成立情况下，我们的样本数据应该是什么样子，在假设不成立的情况下样本数据应该是什么样子，对吧！
举个例子来说吧，给定一组数据，1，2，3，4，5，6，7，8。。。。。，然后我说假设这组数据的总体来自于正态分布，那其实我们要去做的其实就是比较，这组数据和真正正态分布下的产生的数据一些特征，以此来判断这个假设是否正确，即testing。
当然这里例子简单了，一眼看过去，就知道这个假设是应该是错的，因为正态分布最基本的特征就是中间的数据说，两头少，而这堆数据显然是均匀的，自然不会是正态分布！即事实上我们可以观察到是这组数据是“假设不成立”的时候可能得到的样本数据！
这就是假设检验中的，原假设null hypothesis，以及备择假设alternative hypothesis!
继续上面那个例子，即便是1，2，3，4，5，6，7，8。。。。。。，这组数据是不是就一定不可能来自于正态分布总体呢？
emmm，其实也不尽然吧？因为这个数据看上去太离散了，或许正好呢，我们抽样抽到的数据刚好就是那么平均，对吧，严格意义上这也有可能的吧，只不过这种事件发生的概率真的的确太小了。
这里其实引入假设检验中第二个关键的概念：显著水平， significant level = alpha， 即我们在多大程度上会犯错，更确切一点说则是，其实这个是在考虑以下两种情况：

• 事实上假设是对的， 但是我们根据样本计算各种统计量之后给出的推断出现了偏差，即我们拒绝了假设
  
• 事实上假设是错的，但是我们根据样本计算各种统计量之后给出的推断出现了偏差，即我们接受了假设。
  

借用互联网上的一些图来说：


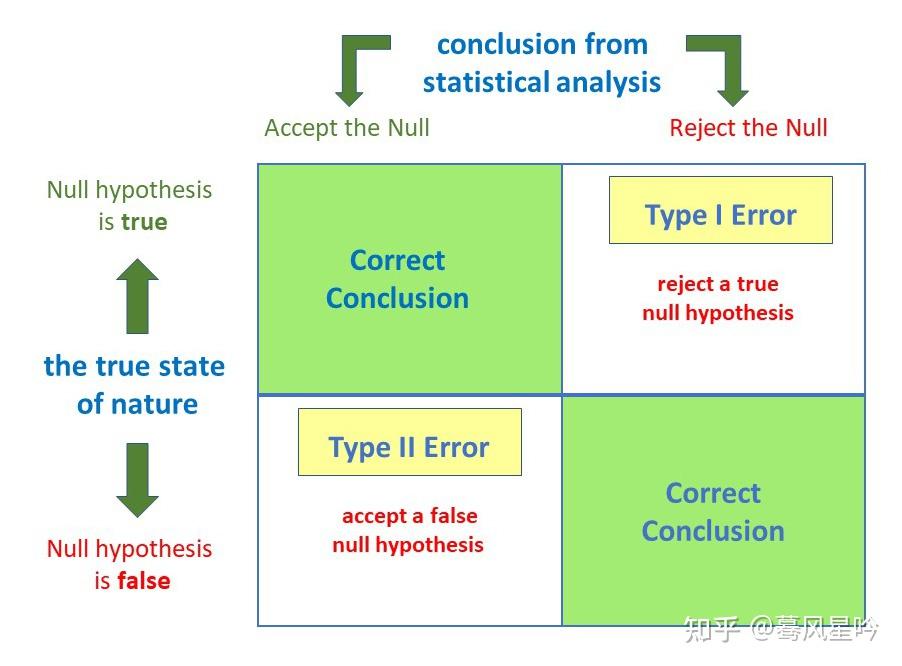
前者的错误被称做是Type 1 error，记作是alpha,也即是我们所说的显著水平（significant level）alpha. 而后者则称作是Type 2 error，一般记作是beta。
其实这两种error其实都是在描述我们在多大程度上会犯错，只不过视角不同，下面这个图就很好的解释了这种差别：


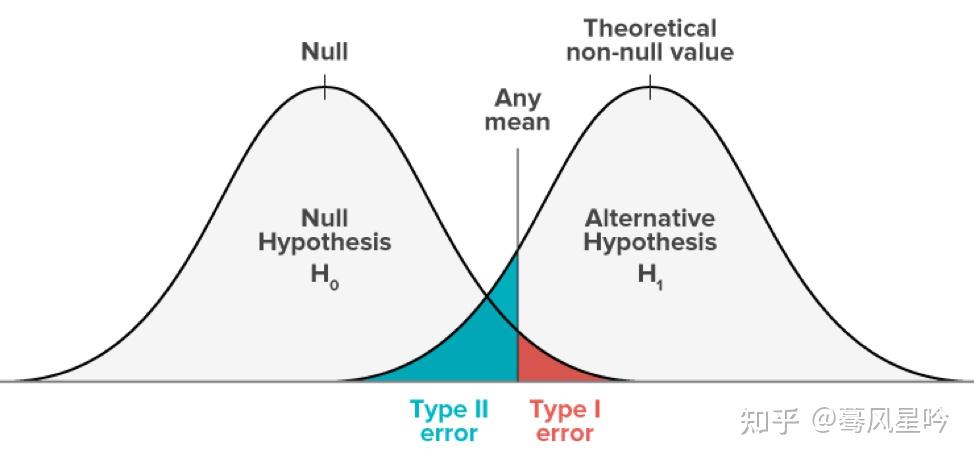
其实这也对应着假设检验中考虑这个问题的角度的不同：

• 第一种情况，Type 1 error。我们其实是在考虑，样本数据是不是会出现在假设总体中的极端情况， 若答案是“YES”， 那就意味着原本的假设是对，只不过我们一顿辛辛苦苦的操作下来，恰好落入了意外会发生的情况中，因而我们给出了错误的结论。
  
• 第二中情况， Type 2 error。我们其实是在考虑， 总体假设不成立的情况下是不是正好恰好意外包含样本数据，若答案是“YES”， 那就意味着原本的假设的总体就是错的，而这种错误又阴差阳错的正好被样本数据计算出来的信息所支持， 因而我们给出了错误的结论。
  

假设检验作为一种科学的统计工具， 之所以科学是因为它不光给出了统计推断的结论，还告诉你了这个结论有多大可能是错的！理论上这种描述其实从alpha看和从beta看其实没有差别，但是通常我们会更多的使用alpha。
这是为什么呢？
原因在于假设检验作为一种统计学工具，最后我们写进论文或者分析报告的肯定是最终的深思熟虑之后的结果，换言之，要是连假设本身就是错的，那这个论文或者报告还谈何深思熟虑呢？所以大多数情况下，最后会写在论文和报告的，事实上都会默认假设是对的，然后去刻画错误，这时候看到就只有Type 1 error啦，所以对应的一般情况我们会更多使用alpha而不是beta。
回到刚才之前那个例子，即给定一组数据，1，2，3，4，5，6，7，8。。。。。，然后我说我要做的假设检验是，这组数据的总体来自于正态分布。这种事情后者说这种愚蠢的操作，理论上并不应该是出现，毕竟如果你数字感觉正常，那么你都不会真的把这个假设作为hypothesis里面的null hypothesis。
当然你非常执着的坚信这个假设，那么在给定一个非常非常大，接近1的alpha的情况下，你仍然可以实用假设假设的全套操作，并且得到一个肯定的结论！
说到这里其实又引出一个概念，检验的效力的问题，即这个所谓的显著水平的问题。如果有人告诉你，这个结论有1%的概率可能是错的，以及， 这个结论有98%概率可能是错的。你一定会觉得后者一定是在逗你玩！
这个统计检验的效率其实会随着alpha的变化而变化， 越小对应的结论正确可能性越大，即效力越高！
其实说了那么多有的没的，或许大多数人来说，假设检验中能记得住可能只有critical value和p-value，所以有人一定会问，为什么你谈了那么多有的没的，为什么还有这两个概念呢？
讲实话，个人觉得如果你能深刻理解上面说的内容的话，这两个概念对你来说肯定是非常自然的！

继续上面说的内容， 现在我们只考虑Type 1 error以及alpha，那么其实我们在考虑研究的重点其实就是个假设总体特征所对应的分布， 如果现在，在给定alpha的情况下（即肯定了总体分布，但是意外落在了总体分布的极端情况下），我们要比较这个总体特征的分布以及样本数据的分布，其实只能有两个途径：

• 从样本数据出发，检查其是否符合总体的特征
  
• 从总体特征出发，检查其是否包含样本数据的情况
  

前者样本数据出发，我们知道在假设检验中我们需要算各种各样的统计量，比如t统计量，z统计量之类的，即根据样本数据与一些公式，总而言之可以算出一个数字来 。根据这个数字 ，我们去following之前说的对总体的假设，自然可以算出这个样本数据出现在总体中的tail里面的概率。这里可以想象一下，一个已知概率密度函数 的分布，给你一个 ,自然可以算出一个概率 ，当然也可以算个积分 ，即可以知道累计密度了，对吧？当然其实更多时候我们一般会曲线救国思想， 即计算 ，更为确切的可以详见wiki：


总而言之，言而总之，反正最后算出来的p，其实就是大名鼎鼎的p-value。记住这个p-value本质就是概率哦！
那么下面我们要做什么呢？
当然是比较这个算出来的p-value与我们之前说给定的alpha啦！
如果小于给定的alpha，也就是说这个样本数据落在了总体假设前提下，不太可能发生的区域，即不太可能发生的发生了，这不就是我们之前讨论的Type 1 error的情况么？ 因此，这也说明了，根据样本数据提供的证据，可以表明样本数据可能是发生了Type 1 error的！从而我们需要拒绝原假设，从而去被迫考虑备择假设。因此，通常我们alpha对应极端情况区域称之为“拒绝域”，一旦落入其中，即拒绝原假设。
第二种考虑问题的方式，即是从总体出发，因为我们已经知道了这个Type 1 error的alpha，即如果是来自是总体的情况，不可能发生但又发生的区域的概率是多少！不光如此，其实我们还假定了总体的分布（或者其特征），固然根据给定累计概率密度，自然可以算法对应的 ,对吧？这里的 也就被称之为critical value. 现在回过头去看，通过样本数据，其实我们可以计算各种各样的统计量，这些形形色色的统计量其本质都是 , 所以本质上critical value就是.
那下面我们要做什么呢？
当然是比较根据样本数据计算得到的统计量与之前根据alpha和分布算出来的critical value啦！
若是统计量大于critical value ， 其说明统计量在critical value的右边，其实看一下图就知道，所谓右边即是刚才所说的拒绝域！若落入拒绝域，当然是要拒绝原假设，从而介绍备择假设啦！



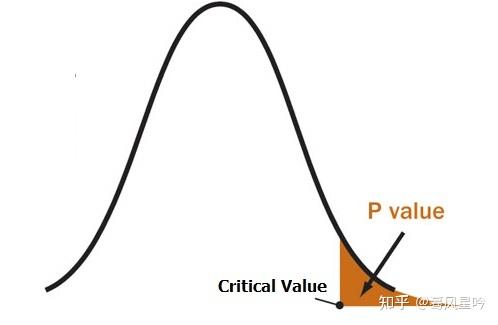
所以本质上来说，p-value与critical value其实是同一张图片，你看的内容不同罢了！
真正理解了就不会出发，反之则说明理解有待加深哦！

假设检验的意义是什么？

所以总的来说，假设检验虽然并不完美，但是它在统计学意义下，为广大定量研究的学科提供了一条非常实用的途径去考察，从“样本”到“总体，”从“猜”到“证”的一个大致框架！这个框架本身是相对科学的，各种的技术细节通常也是有严格的数学保证。

假设检验与参数估计

最后我其实还想说说假设检验与它的孪生兄弟的关系。
我相信大多数中文教材的设置，应该都是会先讲参数估计然后在讲假设检验的吧，当你熟练掌握各种计算和做题技巧后，不知道你是否发现，这两者的操作本质没有差别，只不过是看待问题的角度不同罢了！
什么是参数估计？
当然这是个很大的问题，暂时就不多说了。点估计？区间估计？对，在参数估计中，想必你一定已经算了好多好多的区间估计，同时你也一定已经发现在区间估计中有一个跟显著水平很像的东西， 它叫置信水平confidence level，并且这个数值上来说一般都很大，对吧？对应置信水平的概念就是置信区间啦！
这个置信区间说的是什么呢？
根据我们已有的样本数据， 对于总体中参数的估计，这个估计原来是一个点，考虑到总体分布或者其渐进分布，其实这个点可以扩展成为一个区间，而置信区间在是包括被估计值的一个“大概率”所落在的区域。
这么说的其实有点太抽象了，还是拿之前那个例子，给定数据1,2,3,4,5, 6, 7, 8.......， 现在我们要估计其均值，当然这句话完整来说就是，我们要用样本数据的均值与估计总体的均值！
这里总体的均值其实就是总体中一个参数， 这个这个过程就是参数估计。并且由于统计学的基石，中心极限定理，我们可以得到其渐进分布，大魔王， 正态分布！
完整来说这句话就是说， 这个样本数据的均值这个统计量作为一个随机变量，经过适当标准化后依分布收敛于标准正态分布！这些是极其复杂的东西，这里就不多叙述了，本文重点不在这里哈！
既然现在有了分布，自然我们得到所谓的“极大可能发生的区域”以及“不太可能发生的区域”！对于正态分布来说，2 simga甚至是3 simga原理说的是这个区域是个大概率的区间，即对于标准正态分布，mean+- 1.96*sigma就可以占据原来分布的95%！
那这个95%说明了什么呢？
说明的是总体参数正出现在这个由样本数据估计出来的区间的概率是95%， 换句话说，即总体参数估计没有问题，但是我们的推断错了的概率是5%
因而这里，即显著水平alpha = 5%，置信水平 = 95%！这就是为什么两者相加是1啦！
说回正题，为什么我说两者某种意义下两者是孪生兄弟？

• 因为置信区间可以用来做假设检验！
  

举个例子来说就是，比如检验总体的均值是不是给定的 。这里由于之前说的标准化之后其渐进分布是标准正态分布，
那么自然通过给定alpha之后得到的critical value （这里自然是需要考虑是单侧还是双侧检验啦！一般考虑双侧， ）计算得到其逆标准化后的值就是个范围啦！

那么下面就是去检查那个给定的 究竟是不是在刚才这个关于 的估计的置信区间中呢？
如果在，那就是说明我们可以介绍原假设，反之则拒绝！

2. 在多数时候假设检验过程中计算的内容可以直接被用于构造参数的区间估计
从上面的例子就可以看出，这里的其实不就是给定alpha的时候的critical value么？至于 自然就是个均值统计量啦！至于 其实都会是原问题的给定的哦！

现在抛开上面这些非常粗糙的技术细节，我们仔细来想想，这个区间估计与假设检验的异同：
同： 都是关于总体的参数， 都需要计算统计量，都“可以”实用critical value。
异： 假设检验，从头到尾是个验证的过程，我们的目标是验证假设！而区间估计，或许我们会又一系列假设，但是默认其是对，我们要的是一个参数大概率落在的范围！

PS: 本文并不适合对于假设检验和区间估计零基础的小伙伴！

同花顺

假设检验其实挺好懂：以小概率事件在一次观测中难以出现为基础，尝试接受或拒绝虚无假设（粗糙点说就是什么事情也没发生）的过程。
说起来，在假设检验中，根据实验和测试的要求，可以把100%的概率切成两块（粗糙一些）：

• 备择假设：的确是假设中的变量产生了效应（比如，观测到的差异来自于药物的影响）；
  
• 虚无假设：假设中的变量不能产生效应（比如，观测带的差异来自于随机误差）。
  

毫无疑问，两个假设互斥，概率之和等于1。
那么下面，就要用特定的假设检验方法（比如z-test，t-test，F-test等）计算，在虚无假设为真的假设下，此效应出现的概率。即先假设虚无假设为真（有点奥卡姆剃刀味道），然后计算观察到的效应到底多大概率可以出现。
倘若概率小于临界值（每个学科要求不同），即表明以虚无假设为真作为前提话，这样的结果出现的概率极小（也不是不可以，就是概率太低，比如扔100次正常硬币，次次朝上；你不能否认这可以出现，但是是扔100次一回的话，的确难以出现）。因此，尝试拒绝虚无假设，即接受备择假设。反之，接受虚无假设。

大力水手

我尽量用朴素的语言和简单的例子来说明假设检验。
我们现在有两套搜索引擎，就算是百度和搜狗，想看看哪家搜索做的更好。分别使用5个搜索词到百度和搜狗搜了一下，看了下前10个结果里我们想要的结果有几个。我们用满意度来评价每次搜索的效果，满意度就定义为 想要的结果 / 展示的结果，例如想要的结果有5个，展示结果10个，满意度就是0.5。我们把百度和搜狗的满意度绘制如下表：

搜索词	杨幂	艾尔登法环	JOJO的奇妙冒险	新概念英语	双城之战	均值
百度	0.6	0.4	0.5	0.8	0.3	0.52
搜狗	0.4	0.5	0.3	0.7	0.4	0.46
difference	+0.2	-0.1	+0.2	+0.1	-0.1	0.06

似乎百度的搜索满意度均值高于搜狗的满意度均值，我们可以下结论说，百度搜索做的更好吗？
我们知道生活中有各种各样的随机事件，在搜索这件事上同样可能受到随机因素的影响，我们需要看看百度搜索满意度和搜狗搜索满意度的差异，是不是来自于偶然。（可能在这5个搜索词上搜狗的运气就是差一些呢？）
这时候，我们就不能只看均值了，不如来看看每个搜索词的胜负吧。

搜索词	杨幂	艾尔登法环	JOJO的奇妙冒险	新概念英语	双城之战	胜率
胜负	胜	负	胜	胜	负	0.6

我们并不知道搜索满意度满足什么分布（这是另外一个话题了），我们不如认为这世界上有一个无上意志，每次搜索的时候，他就会掷一次骰子，骰子正面则让百度胜，骰子反面则让百度负。那我们来算算掷5次骰子，其中正面次数大于3次的累积概率（p-value的定义，单侧检验）：

大跌眼镜的事情发生了，p-value是0.5 > 0.05，百度和搜狗没有显著的差异。因为之前观察到的差异完全可以用掷骰子解释。
上面做的事情就是假设检验，假设检验里的非参数检验方法 - 符号检验（sign test)
无论什么样的假设检验方法，本质上都是在验证我们看到的数据，是不是来自于偶然（随机）。

队长是我

谢邀。
假设检验(hypothesis testing)用的方法是“反证法”，原理是“小概率事件原理”，即小概率事件在我们日常观察中一般是不会发生的。
比如我们上学的时候都可能会遇到这样的事情，因为教室里人比较多，老师点一次名需要10多分钟，那么老师就说我会随机抽一次点名，但是如果那一次你没有到，那么算你一直没有来，可能平时分就要没了。那为什么会这样？其实这就是“小概率事件原理”，如果你经常去，那么发生“点名那次恰好不在”这件事的概率是非常小的。
假设检验也是这样子，你先做出假设，然后通过你的样本(SRS), 算得假设的概率是多少，也就是常说的P-Value（probability value）。而显著性水平(significance level， )就是你认为的小概率事件发生的概率大小。
如果 也就是小概率事件发生了，那么我们认为这是不正常的，因为样本是简单随机样本，我们随机取一组样本就发生了，天下没有那么凑巧的事，所以我们就认为假设错误，于是reject null hypothesis。