关于高中的“独立性检验”

幸福侠侣

关于“独立性检验”
高二下学期，讲到统计最后一章“独立性检验”的时候，老师给出了统计量 的计算公式，也就是每次考试都会在大题里恶心你计算的一个式子，它长成这样：
\chi^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}
上式中的各个字母也就是一个2×2列联表里的：

X=0	X=1	总和
Y=0	a	c	a+c
Y=1	b	d	b+d
总和	a+b	c+d	n=a+b+c+d

但有意思的是，这个公式从何而来？为什么它能去“检验独立性”？这是本篇文章试图去解释清楚的两个问题。
首先，我们需要弄清楚“检验独立性”的对象是谁？其实回看课本我们不难发现，独立性检验一般安排在第三节，前两节分别是成对数据的统计相关性和一元线性回归模型，这两个工具的对象都是数值变量，也就是它们的取值是实数，大小和运算是有实际意义的。



湘教版高中数学选择性必修第二册

但很多时候我们很难对一种现象进行“量化”，比如我们去调查听情歌是否会让人想谈恋爱，那问卷的选项无非是“不想”“想”或许有时候还会有“特别想”这种选项，但本篇文章主要讨论2×2的情况，所以先将情况简化，分为“想谈恋爱”“不想谈恋爱”“听情歌”“不听情歌”这四种。为了方便在数学的角度上描述问题，我们引入了一种新的变量，称为分类变量。为了方便区分，我们给分类变量编上号，比如想谈恋爱为Y=1，那么不想谈恋爱就是Y=0 。显然这里的数值并不能说明什么东西，如果你愿意的话，你可以把想谈恋爱规定为Y=π，不想谈恋爱规定为Y=e。方便起见，我们沿用前者。我们将听情歌记为X=1，不听情歌规定为X=0。
像它的名字一样，我们计算这个统计量是为了去检验独立性，也就是去判断这两个变量是独立无关的还是有关联能够相互影响的。直接去判断好像没什么思路，所以我们先提出一个假设：
H_0:听情歌与想谈恋爱无关
换句话说，这是在假设听情歌与想谈恋爱是独立的，我们假设听不听情歌跟想不想谈恋爱没关系，那么你想谈恋爱的概率不会因为你听情歌就上升。转换成数学语言，也就是：
H_0:\ \ P(Y=1\ | \ X=1)=P(Y=1\ | \ X=0)
这个式子是在说，听情歌时，我想谈恋爱的概率和不听情歌时我想谈谈恋爱的概率是相等的。这个跟我们一开始用自然语言说的假设是等价的。那么根据条件概率的相关知识，我们能推导出如果 H_0 成立，那么下面的式子也成立：
首先根据条件概率的定义：
P(Y=1\ | \ X=1)=P(Y=1\ | \ X=0) \Rightarrow \frac{P(Y=1,X=1)}{P(X=1)}=\frac{P(Y=1,X=0)}{P(X=0)}=\frac{P(Y=1)P(X=0\ |\ Y=1)}{P(X=0)}  
由于X=1与X=0是对立事件，所以
P(X=1)=1-P(X=0)   
P(X=0\ |\ Y=1)=1-P(X=1\ |\ Y=1)  
代入上式
\frac{P\left(Y=1,X=1\right)}{P\left(X=1\right)}=\frac{P\left(Y=1\right)\left[1-P\left(X=1\ |\ Y=1\right)\right]}{1-P\left(X=1\right)}  =\frac{P\left(Y=1\right)-P\left(Y=1,X=1\right)}{1-P(X=1)}  
交叉相乘一下
P\left(Y=1,X=1\right)-P\left(X=1\right)P\left(Y=1,X=1\right)  
=
P\left(X=1\right)P\left(Y=1\right)-P(X=1)P\left(Y=1,X=1\right)  
会发现等式两边的 P\left(X=1\right)P\left(Y=1,X=1\right) 消掉了，留下来了最后的精华：
P\left(Y=1,X=1\right)=P(X=1)P(Y=1)
说明一下， P\left(Y=1,X=1\right) 就是Y=1且X=1发生的概率，也就是听情歌且想谈恋爱的情况。这个结论直接利用两个事件独立的定义也可以得到，湘教版的教材直接利用了定义，而人教版的教材是这样子给出 H_0 的等价形式，这里的推导也是为了方便说明X=1与Y=1独立等价于X=1与Y=0独立，X=0与Y=1独立，X=0与Y=0独立。
那么按照 H_0 的假设方法，我们也能得到其它三个等价假设：
P\left(Y=1,X=0\right)=P(X=0)P(Y=1)   
P\left(Y=0,X=1\right)=P(X=1)P(Y=0)   
P\left(Y=0,X=0\right)=P(X=0)P(Y=0)  
根据我们的统计问卷，我们可以得到下列的表：

X=0	X=1	总和
Y=0	a	c	a+c
Y=1	b	d	b+d
总和	a+b	c+d	n=a+b+c+d

因为我们假设 H_0 成立，由频率稳定于概率的原理，我们能算出：
P\left(X=1\right)P\left(Y=1\right)=\frac{\left(c+d\right)\left(b+d\right)}{n^2}   
P\left(Y=1,X=1\right)=\frac{d}{n}  
为了方便计算，我们考虑二者的频数，毕竟可以少除一个n，我们把前者的频数称为频数的期望值，也就是说成立时我们希望我们调查问卷中的频数是这个值，也就是让d 这个实际频数很接近我们的期望频数，这样的话就说明我们的假设是对的，想谈恋爱和听情歌是没有关系的。也就是说
|d-\frac{\left(c+d\right)\left(b+d\right)}{n}|
这个值要足够小，那么同理，我们可以得到其它三个表达式也要足够小，也就是
|a-\frac{\left(a+b\right)\left(a+c\right)}{n}|
|b-\frac{\left(a+b\right)\left(b+d\right)}{n}|
|c-\frac{\left(a+c\right)\left(c+d\right)}{n}|  
这三个值要足够小，就能说明我们的假设是成立的
好，这离我们的卡方独立性检验的公式已经很接近了，最后我们要考虑的，是将这四个值统一在一起，我们先考虑将四者直接相加，但由于绝对值的本身不具有很好的性质（这一点在最小二乘法里大家应该有所体会，最小二乘法里的 \hat{a} 和 \hat{b} 的计算公式就是利用了平方求导的简便性，还有在规定方差时用的也是平方而非绝对值），所以我们先选择将前文的四者平方后加一块。
\left[a-\frac{\left(a+b\right)\left(a+c\right)}{n}\right]^2+\left[b-\frac{\left(a+b\right)\left(b+d\right)}{n}\right]^2+ \left[c-\frac{\left(a+c\right)\left(c+d\right)}{n}\right]^2+\left[d-\frac{\left(c+d\right)\left(b+d\right)}{n}\right]^2  
但人教版的课本中给四个项都除以了它们期望值，理由是当样本数据过多时，算出来的期望值过大，那么你这个“小”可能相对于你的样本数量级已经很小了，但是客观来看还是有点大，这不能使得我们的统计检验量成为一个“普适”的工具，所以通过除以期望值来减少样本量的影响，我觉得这是一个合理的解释。
也就是:
\chi^2=\frac{\left[a-\frac{\left(a+b\right)\left(a+c\right)}{n}\right]^2}{\frac{\left(a+b\right)\left(a+c\right)}{n}} +\frac{\left[b-\frac{\left(a+b\right)\left(b+d\right)}{n}\right]^2}{\frac{\left(a+b\right)\left(b+d\right)}{n}} +\frac{\left[c-\frac{\left(a+c\right)\left(c+d\right)}{n}\right]^2}{\frac{\left(a+c\right)\left(c+d\right)}{n}} +\frac{\left[d-\frac{\left(c+d\right)\left(b+d\right)}{n}\right]^2}{\frac{\left(c+d\right)\left(b+d\right)}{n}}  
上文大都是对课本的解读，接下来的部分就是关于这个式子如何化简的问题。首先，我们观察每一个式子中的“差值”部分
a-\frac{\left(a+b\right)\left(a+c\right)}{n}=\frac{\left[na-\left(a+b\right)\left(a+c\right)\right]}{n} =\frac{\left[\left(a+b+c+d\right)a-\left(a+b\right)\left(a+c\right)\right]}{n}=\frac{\left[\left(c+d\right)a-\left(a+b\right)c\right]}{n} =\frac{ad-bc}{n}  
    对于上面四个部分的分子，算出来的差值的平方应该是“相同的”，因为都是和对角线的值的乘积减去另一个对角线的乘积，然后平方就不用担心正负的问题了。那么，我们的独立性检验的公式就可以写成：
\chi^2=\frac{\left(ad-bc\right)^2}{n}\bullet \left[\frac{1}{\left(a+b\right)\left(a+c\right)}+\frac{1}{\left(a+b\right)\left(b+d\right)}+\frac{1}{\left(a+c\right)\left(c+d\right)}+\frac{1}{\left(c+d\right)\left(b+d\right)}\right]
=\frac{\left(ad-bc\right)^2}{n}\bullet[\frac{\left(c+d\right)\left(b+d\right)+\left(a+c\right)\left(c+d\right)+\left(a+b\right)\left(b+d\right)+\left(a+b\right)\left(a+c\right)}{\left(a+b\right)\left(a+c\right)\left(b+d\right)\left(c+d\right)}]
=\frac{\left(ad-bc\right)^2}{n}\bullet[\frac{\left(c+d\right)n+\left(a+b\right)n}{\left(a+b\right)\left(a+c\right)\left(b+d\right)\left(c+d\right)}]
=\frac{\left(ad-bc\right)^2}{n}\bullet[\frac{n^2}{\left(a+b\right)\left(a+c\right)\left(b+d\right)\left(c+d\right)}]
=\frac{{n\left(ad-bc\right)}^2}{\left(a+b\right)\left(a+c\right)\left(b+d\right)\left(c+d\right)}
写到这，那么接下来的检验就很简单了，我们只需要把值代进去一算，看算出来的 \chi^2 是“较大”还是“较小”。如果较小，说明我们有理由去说明假设 H_0 是成立的，如果较大，那说明我们没有足够的理由去说明 H_0 是不成立的，也就是说，谈恋爱是跟听情歌有关系的。关于较大较小是如何判断的，考试时会贴心地给你一张表，但这个表是如何算出来的，这就涉及到一些本科的知识了。接下来的是拓展内容， \chi^2 的概率分布服从一个名为卡方分布的东西，它的概率密度函数长这样：
P\left(\chi^2\right)=\frac{1}{2^\frac{n}{2}\Gamma(n/2)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}
其中n是自由度，数学家已经证明了在 H_0 成立的前提下，我们在两个分类变量下算出来的 \chi^2 服从n=1的卡方分布， \Gamma(x) 是gamma函数，它长成这个样子：
\Gamma\left(x\right)=\int_{0}^{+\infty}{x^{n-1}e^{-x}dx}
所以：
P\left(\chi^2\right)=\frac{1}{\sqrt2\Gamma(1/2)}x^{-\frac{1}{2}}e^{-\frac{x}{2}}
它的图像大概长这样：



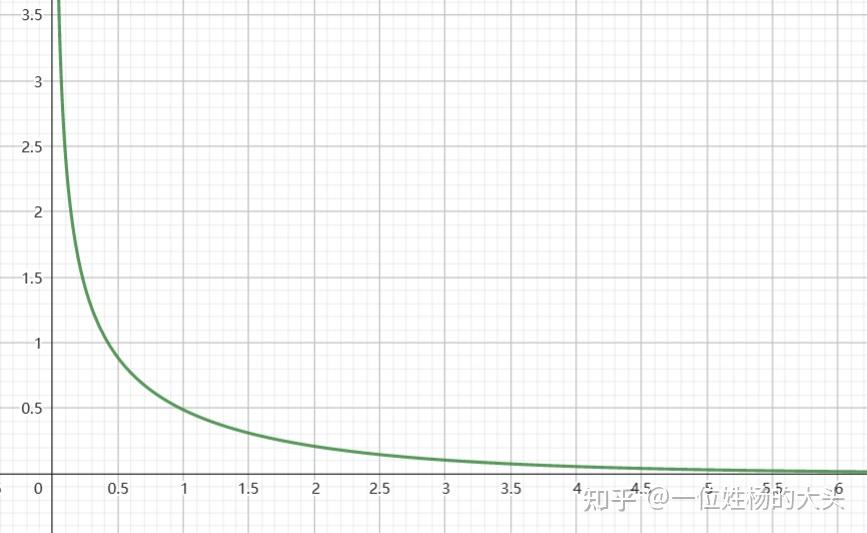
cr：geogebra

回到前面的问题，如何去判断我们计算出的卡方值是较大还是较小呢？就需要我们设定一个值 x_0 ，当我们算出的卡方值大于 x_0 时，我们就拒绝 H_0 ；如果小于 x_0 ，说明我们没有足够的理由拒绝 H_0 ，就接受。
那么 P\left({\ \chi}^2\geq x_0\right)=\int_{x_0}^{+\infty}{P({\ \chi}^2)}dx ，其实不用被积分符号吓到，就把它和正态分布类比，就是图像底下的面积，其中积分号告诉你了是哪里到哪里的面积，这里是 x_0 到正无穷。回到这个公式，它是在说， H_0 成立的前提下，你算出的 {\ \chi}^2\geq x_0 的概率是 \int_{x_0}^{+\infty}{P({\ \chi}^2)}dx ，那么，当我们算出来的 {\ \chi}^2\geq x_0 时，我们拒绝 H_0 时犯错误的概率就是 \int_{x_0}^{+\infty}{P({\ \chi}^2)}dx ，为什么？犯错误是指 H_0 成立但是我们认为它不成立，此时 H_0 成立的概率就是 \int_{x_0}^{+\infty}{P({\ \chi}^2)}dx
根据我们的直觉，当卡方值算出来很大时，我们可以去选择更大的 x_0 ，使得图像下的面积越来越小，也就是 H_0 成立的概率也会很小，那么拒绝 H_0 时我犯错误的概率就会更小了。
其实我们也可以先选定我们可以接受的犯错误的概率，反求出 x_0 ，然后看我们计算出的 \chi^2 是否大于 x_0 ，和上面的做法是差不多的。
这就是这篇文章的全部了，很感谢各位能看到这里，在最后我想说的是，在高中，我们往往觉得统计不是那么的重要，就像弄懂卡方检验的公式没有什么必要，知道卡方分布好像对高考也没什么帮助。但我觉得，对某种事物的追求是我活着的证明，在写这篇文章的时候，我尝试着去解释一些细枝末节的问题，像是为什么卡方检验用的是平方而不是绝对值，为什么要各项要除以期望值。在追寻这些问题的答案时，我真切地感受到活着，体会到一种收获知识并想把这一份知识传递给他人的激动。死亡诗社里说诗，美，浪漫，爱，是我们生存的原因。我想数学也是如此散发着美丽，吸引着从古至今的人俯首称臣，前仆后继。
谢谢大家。

原文地址：https://zhuanlan.zhihu.com/p/634777437