主成分分析(principal component analysis)

风云

一、主成分分析的思想
  主成分分析是数据处理中常用的降维方法。我们需要处理的数据往往是高维数据，把它看成是由某个高维分布产生。高维分布的不同维之间可能具有较强的相关性，这也就为数据降维提供了可能。为了叙述清楚主成分分析的思想，我们通过二维数据进行叙述，即数据是由随机向量 (X_1,X_2) 产生，并假设 X_1=X_2 。通过该分布得到的样本点如图下所示：


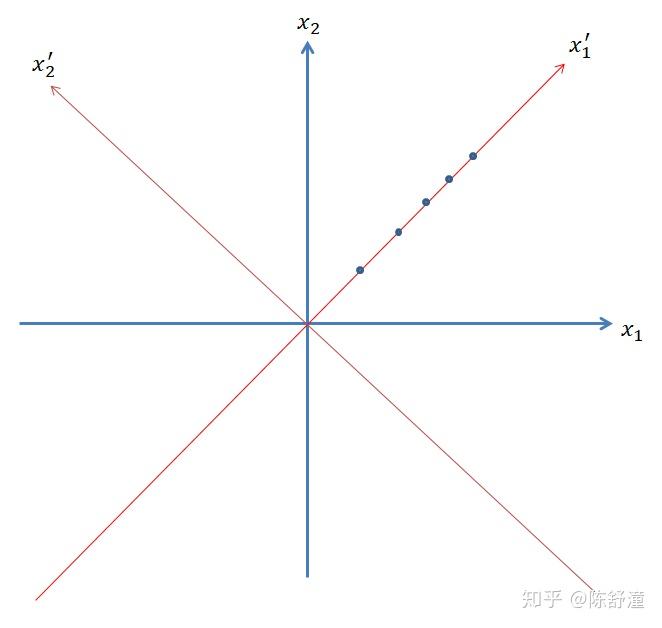
如果我们把每个数据点用 (x_1,x_2) 表示，那么，每个数据是二维的。实际上，容易发现，我们只需要将坐标系进行旋转，旋转到红色坐标系位置，此时，每个数据点在新坐标系下的表示形式为为 (x_1^{'},0) ，由于每个数据点的第二维坐标都是 0 ，所以每个数据点只需要用一个数表示就行了，这样就把数据的维数从二维降到了一维。接下来考虑不是完全线性关系，但是具有强相关性的情况，如下图所示：


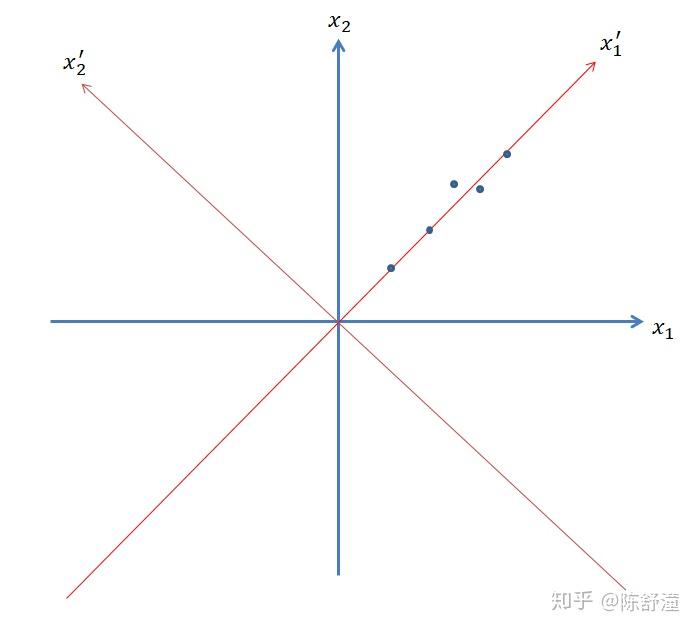
在这种情况下，我们不可能通过坐标系的平移与旋转，使所有点都落在一根轴上，即不可能精确地把数据用一维表示。但是注意到 (X_1,X_2) 仍然有强相关性，我们仍然将坐标轴旋转到红色位置，可以看出，将数据在 x_1^{'} 上的投影近似代表原数据，几乎可以完全反映出原数据的分布。直观看，如果要将数据投影到某根轴，并用投影来表示原数据，将数据压缩成一维，那么投影到 x_1^{'} 是最好的选择。因为投影到这跟轴，相比于投影到其他轴，对原数据保留的信息量最多，损失最小。如何衡量保留的信息量呢？在主成分分析中，我们用数据在该轴的投影的方差大小来衡量，即投影后方差越大（即投影点越分散），我们认为投影到该轴信息保留量最多。从这种观点看，投影到 x_1^{'} 确实是最好的选择，因为投影到这根轴，可使得投影点最分散。我们将数据的中心平移到原点（即新坐标轴的原点在数据的中心位置），为了消除单位的影响，我们将数据的方差归一化。进一步考虑如下数据分布：


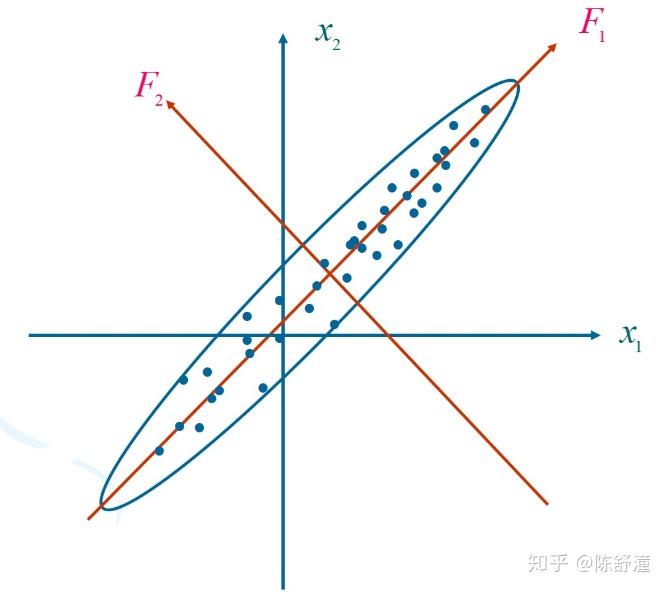
根据上述，如果要将数据压缩为一维的，那么应该选择 F_1 轴进行投影，如果用该投影表示原数据的损失过大，我们可以再选择第二根轴进行投影，第二根轴应该与 F_1 垂直（保证在两根轴上的投影是不相关的）并且使得数据在该轴上投影方差最大，即图中的 F_2 轴（如果是二维情况，第一根轴确定后，第二根轴就确定了。但是对于三维情况，第一根轴确定后，第二根轴在与第一根轴垂直的平面内选取，这样的选取方式有无穷多种，通过投影最大来确定第二根轴在该平面内的选取方式。高维空间同理），这样，每个数据点由原来的用在 x_1,x_2  轴下的坐标表示变成了用在 F_1,F_2 下的坐标表示。 F_1,F_2 的方向依次称为第一主成分方向，第二主成分方向。数据在 F_1,F_2 上的投影依次称为该数据的第一主成分，第二主成分。容易看出， n 维数据有 n 个主成分。

二、随机向量的主成分
1、随机向量的主成分的定义与计算
  由上述例子受到启发，我们先对随机向量的主成分进行定义。假设随机向量为 X=(X_1,X_2...X_n)^T ,轴 l 的单位方向向量 l=(l_1,l_2...l_n)^T ，那么随机向量 X 的在轴 l 上的投影为 X_l=l^TX ，该投影随机变量的方差 D(X_l)=D(l^TX)=l^{T}\Sigma l ，其中 \Sigma 是 X 的协方差矩阵。由上述讨论，给出随机向量的主成分的定义如下：
定义一、随机向量的主成分的定义：对于 n 维空间的随机向量 X=(X_1,X_2...X_n)^T
(1)、在 n 维空间中寻找一个方向 \alpha_1 ，使得 X 在该方向上投影的方差最大，该方向称为第一主成分方向， X 在该方向上的投影称为 X 的第一主成分
(2)、在与 \alpha_1 正交的所有方向中，寻找一个方向 \alpha_2 ，使得 X 在该方向上投影的方差最大，该方向称为第二主成分方向， X 在该方向上的投影称为 X 的第二主成分。
...如此归纳下去：
(n)、在与 \alpha_1,\alpha_2...\alpha_{n-1} 正交的所有方向中，寻找一个方向 \alpha_n ，使得 X 在该方向上投影的方差最大，该方向称为第 n 主成分方向， X 在该方向上的投影称为 X 的第 n 主成分。
下面定理给出了求解 n 个主成分方向的方法：
定理一、设X 的协方差矩阵 \Sigma 的特征值为： \lambda_1\geq\lambda_2\geq...\geq\lambda_n\geq0 ，对应的单位特征向量记为 \alpha_1,\alpha_2...\alpha_n 。则
(1)、 \alpha_k 恰好为第 k 主成分的方向
(2)、 \lambda_k 恰好为第 k 主成分的方差
(3)、 X 的第 k 主成分为 \alpha_k^{T}X
我看过的所有机器学习、多元统计分析的书，都是构造拉格朗日函数，利用微积分的方法（对向量求偏导求极值）证明。我并不喜欢在纯线性变换中应用微积分去计算最值，下面我给出一种线代证法。
首先证明:在由 \alpha_k,\alpha_{k+1}...\alpha_n 张成的特征空间中，使得 l^{T}\Sigma l 取到最大值的单位向量 l 就是 \alpha_k ，且投影方差的最大值 \alpha_k^{T}\Sigma\alpha_k=\lambda_k
证明、对于该特征空间的任意单位向量 l ，存在 c_k,c_{k+1}...c_n ，使得
l=c_k\alpha_k+c_{k+1}\alpha_{k+1}+...+c_n\alpha_n ，由 (l,l)=1 与 (\alpha_i,\alpha_i)=1\;(k\leq i\leq n) 知 c_k^{2}+c_{k+1}^{2}+...+c_n^{2}=1 。
l^{T}\Sigma l=(c_k\alpha_k+c_{k+1}\alpha_{k+1}+...+c_n\alpha_n)^T\Sigma(c_k\alpha_k+c_{k+1}\alpha_{k+1}+...+c_n\alpha_n)=
(c_k\alpha_k+c_{k+1}\alpha_{k+1}+...+c_n\alpha_n)^T(\lambda_k c_k\alpha_k+\lambda_{k+1} c_{k+1}\alpha_{k+1}+...+\lambda_nc_n\alpha_n)=
\lambda_kc_k^{2}+\lambda_{k+1}c_{k+1}^2+...+\lambda_nc_n^{2}\leq \lambda_k(c_k^{2}+c_{k+1}^{2}+...+c_n^{2})=\lambda_k
当且仅当 l=a_k 取等号。我们利用这个结论立即可以得到 n 个主成分计算方法,将 n 个主成分方向记为 l_1,l_2...l_n ，则：
（1）第一主成分是在全空间寻找 l_1 使得 l_1^{T}\Sigma l_1 最大，全空间可以看成是由特征向量 \alpha_1...\alpha_n 张成的，由上述定理，当 l_1=a_1 时，方差 l_1^{T}\Sigma l_1 最大，最大值为 \lambda_1
（2）由实对称矩阵的性质，与 a_1 正交的空间恰好可以由 \alpha_2...\alpha_n 张成，由上述定理，当 l_2=a_2 时，方差 l_2^{T}\Sigma l_2 最大，最大值为 \lambda_2
（3）与 \alpha_1,\alpha_2 均正交的空间恰好可以由 \alpha_3...\alpha_n 张成，由上述定理，当 l_3=a_3 时，方差 l_3^{T}\Sigma l_3 最大，最大值为 \lambda_3
该过程进行 n 次，定理证毕。
记矩阵 A=(\alpha_1,\alpha_2...\alpha_n) ，则 Y=A^TX 是 X 的 n 个主成分（第 k 行为第 k 个主成分）。

2、随机向量的主成分的性质
这些性质的证明极其简单，下面不给出证明，只叙述结论：
(1)、 Y 的各分量是不相关的（这就是要取正交系的原因），即 Y 的协方差矩阵是对角阵，
cov(Y)=diag(\lambda_1,\lambda_2...\lambda_n)
(2)、 n 个主成分的方差之和等于 X 的各分量的方差之和，即用 n 个主成分（所有主成分）来表示原数据是不损失信息量的。使用主成分分析，方差较大的方向（即信息量较大的方向）集中在前面较少的几个方向中，因此可以用前面较少的方向来近似表示原数据，使得数据信息量损失较少，从而实现降维。

三、基于主成分分析的最佳逼近
现在需要将 n 维数据压缩成 q 维，并使得保留的信息最大（即 q 个方向的方差总和最大），考虑如何选取这 q 个方向。需要注意的是，现在并不能说这 q 个方向就是前 q 个主成分方向 \alpha_1,\alpha_2...\alpha_q ，因为这里我们需要同时确定 q 个方向，在主成分分析中，是逐个确定方向的，不排除这个可能性：存在另外的 q 个方向 \beta_1,\beta_2...\beta_q ，虽然 X 在 \alpha_1 上的投影方差比在 \beta_1 上的大，但是在后面某些 \beta 上的投影方差比在对应的 \alpha上的大，使得在 \beta_1,\beta_2...\beta_q 上的投影方差总和比在 \alpha_1,\alpha_2...\alpha_q 上的方差总和大。下面定理说明，这是不可能的。
定理二、要在n 维空间确定 q 个正交的投影方向，使得 X 在这 q 个方向的投影方差总和最大，则这 q 个方向恰好是 X 的前 q 个主成分方向。
证明、假设矩阵 B_{m\times q} , B 的列向量组是两两正交的 n 维向量，每个列是一个投影方向，则 X 在 q 个方向上的投影为： B^TX ，它的第 i 行为 X 在第 i\;(1\leq i\leq q) 个方向的投影。随机向量 B^TX 的协方差矩阵为 B^T\Sigma B ，在 q 个方向的方差总和为 tr(B^T\Sigma B) 。现问题归结为求矩阵 B ，使得 tr(B^T\Sigma B) 最大。与上文一样，令 A=(\alpha_1,\alpha_2...\alpha_n) ，则存在矩阵 C ，使得 B=AC 。
tr(B^T\Sigma B)=tr(C^TA^T\Sigma AC)=tr(C^T\Lambda C)=tr(\sum_{j=1}^{n}\lambda_jc_jc_j^{T})=\sum_{j=1}^{n}\lambda_jtr(c_jc_j^{T})
=\sum_{j=1}^{n}\lambda_jtr(c_j^{T}c_j)=\sum_{j=1}^{n}\sum_{k=1}^{q}\lambda_jc_{jk}^{2}=\sum_{j=1}^{n}(\lambda_j\sum_{k=1}^{q}c_{jk}^{2})\;\;\;\;\;\;(1)
其中 c_j 是 c 的第 j 列。
由于 A 是正交阵，那么 C=A^TB ， C^TC=B^TAA^TB=B^TB=I_q ，所以 C 的列向量组也是正交的。于是
tr(C^TC)=q
即 \sum_{j=1}^{n}\sum_{k=1}^{q}c_{jk}^{2}=q\;\;\;\;\;\;(2)
由扩充定理，可以找到矩阵 D ，使得 [C,D] 构成一个正交矩阵，记该矩阵的第 j 行为 d_j ，则 d_jd_j^{T}=1 ，又 c_jc_j^{T}\leq d_jd_j^{T} ，所以 c_jc_j^{T}\leq 1 ，即
\sum_{k=1}^{q}c_{jk}^2\leq1\;\;\;\;\;\;\;(1\leq j\leq n)\;\;(3)
令 \sum_{k=1}^{q}c_{jk}^{2}=a_j\;\;\;\;\;\;(1\leq j\leq n) ，则 (1)(2)(3) 可改写为如下形式：在如下约束条件：
\lambda_1\geq \lambda_2\geq...\geq\lambda_q\geq...\geq\lambda_n
0\leq a_j\leq1
\sum_{j=1}^{n}a_j=q
下，求 a_j 使得 \sum_{j=1}^{n}\lambda_ja_j 最大。显然当 a_j=1\;(1\leq j\leq q),a_j=0\;(q\leq j\leq n) 时取到最大值，此时当且仅当 B 的列向量组是 \alpha_1,a_2...a_q ，在不考虑排列顺序的情况下，矩阵 B 是唯一的。证毕。
定义二、第 k 个主成分 y_k 的方差（信息）贡献率为 y_k 的方差与总方差之比，记为 \eta_k ，
\eta_k=\frac{\lambda_k}{\sum_{i=1}^{n}\lambda_i} 。 k 个主成分累计方差贡献率定义为 k 个方差之和与所有方差之和的比，即 \sum_{i=1}^{k}\eta_i=\frac{\sum_{i=1}^{k}\lambda_i}{\sum_{i=1}^{n}\lambda_i} .
通常 取 k 值使得累计方差贡献率达到给定的百分比以上，累计贡献率反映了主成分保留信息的比例。

四、样本主成分分析
样本主成分分析与整体主成分分析完全类似。只需要将上文的整体协方差矩阵 \Sigma 用样本协方差矩阵 S 代替即可。通过计算 S 的n 个单位特征向量的方向，就可以得到该数据的 n 个主成分方向。将样本往这些方向投影，即可得到该样本的各个主成分。证明与结论与随机向量的主成分分析完全一致，不再赘述。
PS、样本协方差矩阵 S 是总体协方差矩阵 \Sigma 的一个无偏估计，样本相关矩阵是总体相关矩阵的一个无偏估计， S 的特征值和特征向量是 \Sigma 的特征值与特征向量的最大似然估计。证明参考多元统计教材。
由于主成分分析只是数据降维的一种方法，即数据预处理的一种方法。这里不给出实现。后面的文章将会给出结合主成分分析与朴素贝叶斯分析，对手写数字图片进行识别的例子。

原文地址：https://zhuanlan.zhihu.com/p/150097862