时间序列单位根检验(1)：DF/ADF/PP检验统计量计算

心中u你

文章题图来源SAS单位根检验 - SAS专版 - 经管之家(原人大经济论坛)
时间序列的单位根检验用于判断时间序列的平稳性，目前已经构成一个庞大的体系，方法众多。多数时间序列分析教材都会叙述DF（Dickey and Fuller，1979）、ADF（augmented Dickey-Fuller，1981）、PP（Phillips and Perron,1988）三种检验方法，但大多数叙述都侧重于对如何应用SAS、Eviews等软件的介绍，缺乏计算细节。最近在项目造轮子过程中研究了相应的计算方法，总结如下（对照可以实现和SAS一样的计算结果）：
（1）DF检验统计量计算
①普通AR(1)过程
y_{t}=\rho y_{t-1}+\varepsilon_{t}
H_{0}:|\rho |\geq1\ vs\ H_{1}:|\rho|<1
检验统计量 t=\frac{\hat{\rho}-1}{\hat\sigma_{\rho}}
计算检验统计量采用最小二乘法，设样本 Y_{T}=（y_{1},y_{2},...,y_{T})
记 X=(y_{1},y_{2},...,y_{T-1})\ ,Y=(y_{2},y_{3},...,y_{T})
容易得到 \hat\rho=\frac{l_{xy}}{l_{xx}} , \hat\sigma_{\rho}=(\frac{s_{t}}{l_{xx}})^{\frac{1}{2}}
s_{t}=\frac{1}{T-2}\Sigma_{i=1}^{T-1}(y_{i}-\hat y_{i}) ， \hat y_{i}=\hat\rho x_{i}，i=1,2,...,T-1

②带漂移项的AR(1)过程
y_{t}=\rho y_{t-1}+a+\varepsilon_{t}
原假设和检验统计量同上
记 X=\begin{bmatrix} 1 & y_{1}\\ 1 & y_{2}\\ \vdots & \vdots \\ 1 & y_{T-1} \end{bmatrix}，Y=(y_{2},...,y_{T})&#39;
则 \begin{bmatrix} \hat a \\ \hat\rho \end{bmatrix} =(X&#39;X)^{-1}X&#39;Y
\hat \sigma_{\rho}= (s_{t} \begin{bmatrix} 0 & 1 \end{bmatrix} (X&#39;X)^{-1} \begin{bmatrix} 0\\ 1 \end{bmatrix} )^{\frac{1}{2}}
s_{t}=\frac{1}{T-3}\Sigma_{i=1}^{T-1}(y_{i}-\hat y_{i}) ， \hat y_{i}=\hat\rho x_{i2}+\hat a，i=1,2,...,T-1

③趋势平稳AR(1)过程
y_{t}=\rho y_{t-1}+a+\beta t+\varepsilon_{t}
原假设和检验统计量同上
记 X=\begin{bmatrix} 1 & y_{1} & 2\\ 1 & y_{2} & 3\\ \vdots & \vdots &\vdots \\ 1 & y_{T-1} &T \end{bmatrix}，Y=(y_{2},...,y_{T})&#39;
则 \begin{bmatrix} \hat a \\ \hat\rho \\ \hat\beta \end{bmatrix} =(X&#39;X)^{-1}X&#39;Y
\hat \sigma_{\rho}= (s_{t} \begin{bmatrix} 0 & 1 &0 \end{bmatrix} (X&#39;X)^{-1} \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix} )^{\frac{1}{2}}
s_{t}=\frac{1}{T-4}\Sigma_{i=1}^{T-1}(y_{i}-\hat y_{i}) , \hat y_{i}=\hat\rho x_{i2}+\hat a +\hat\beta x_{i3}，i=1,2,...,T-1

（2）ADF检验统计量计算
ADF即为“增广的”Dickey-Fuller检验，对于一个AR(p)模型，可以将其改写成以下形式
y_{t}=\Sigma_{i=1}^{p}\phi_{i}y_{t-i}+\varepsilon_{t} =\rho y_{t-1}+\Sigma_{i=1}^{p-1}\zeta_{i}\Delta y_{t-i}+\varepsilon{t}  
可以证明 \rho =\Sigma_{i=1}^{p} \phi_{i}
类似（1）的三种情况，ADF检验也有对应的三种情况（显然DF检验是ADF检验在p=1时的特例）
①普通AR(p)过程
标准形式为：y_{t}=\Sigma_{i=1}^{p-1}\zeta_{i}\Delta y_{t-i}+\rho y_{t-1} +\varepsilon{t} =x_{t}&#39;R+\varepsilon{t}
其中 R=(\zeta_{1},...,\zeta_{p-1},\rho)&#39;
H_{0}:|\rho |\geq1\ vs\ H_{1}:|\rho|<1
检验统计量 t=\frac{\hat{\rho}-1}{\hat\sigma_{\rho}}
样本数据集为 Y=(y_{p+1},...,y_{T})&#39;
X= \begin{bmatrix} \Delta y_{2} & \Delta y_{3} & \cdots & \Delta y_{p} & y_{p} \\ \Delta y_{3} & \Delta y_{4} & \cdots & \Delta y_{p+1} & y_{p+1}\\ \vdots & \vdots & \ & \vdots & \vdots \\ \Delta y_{T-p+1} & \Delta y_{T-p+2} & \cdots & \Delta y_{T-1} & y_{T-1} \end{bmatrix}  
则 \hat R =(X&#39;X)^{-1}X&#39;Y
\hat \sigma_{\rho}= (s_{t} e_{i}&#39;(X&#39;X)^{-1} e_{i})^{\frac{1}{2}}
其中： e_{i}=[0,...,0,1]&#39;=(e)_{p \times 1}
s_{t}=\frac{1}{T-2p}(Y-\hat Y)&#39;(Y-\hat Y)，\hat Y =X\hat R

②带漂移项的AR(p)过程
标准形式为： y_{t}=\Sigma_{i=1}^{p-1}\zeta_{i}\Delta y_{t-i}+a+\rho y_{t-1} +\varepsilon{t} =x_{t}&#39;R+\varepsilon{t}
其中 R=(\zeta_{1},...,\zeta_{p-1},a,\rho)&#39;
原假设和检验统计量同上
X= \begin{bmatrix} \Delta y_{2} & \Delta y_{3} & \cdots & \Delta y_{p} & 1& y_{p} \\ \Delta y_{3} & \Delta y_{4} & \cdots & \Delta y_{p+1} & 1 &y_{p+1}\\ \vdots & \vdots & \ & \vdots &\vdots & \vdots \\ \Delta y_{T-p+1} & \Delta y_{T-p+2} & \cdots & \Delta y_{T-1} &1 & y_{T-1} \end{bmatrix}
Y=(y_{p+1},...,y_{T})&#39;
\hat R=(X&#39;X)^{-1}X&#39;Y
\hat \sigma_{\rho}= (s_{t} e_{i}&#39;(X&#39;X)^{-1} e_{i})^{\frac{1}{2}}
其中： e_{i}=[0,...,0,1]&#39;=(e)_{(p+1) \times 1}
s_{t}=\frac{1}{T-2p-1}(Y-\hat Y)&#39;(Y-\hat Y)，\hat Y =X\hat R

③趋势平稳AR(p)过程
原假设和检验统计量同上，标准形式
y_{t}=\Sigma_{i=1}^{p-1}\zeta_{i}\Delta y_{t-i}+a+\beta t +\rho y_{t-1} +\varepsilon{t} =x_{t}&#39;R+\varepsilon{t}
R=(\zeta_{1},...,\zeta_{p-1},a,\beta,\rho)&#39;
X= \begin{bmatrix} \Delta y_{2} & \Delta y_{3} & \cdots & \Delta y_{p} & 1& p+1 & y_{p} \\ \Delta y_{3} & \Delta y_{4} & \cdots & \Delta y_{p+1} & 1 & p+2 &y_{p+1}\\ \vdots & \vdots & \ & \vdots &\vdots &\vdots &\vdots \\ \Delta y_{T-p+1} & \Delta y_{T-p+2} & \cdots & \Delta y_{T-1} &1 & T & y_{T-1} \end{bmatrix}
Y=(y_{p+1},...,y_{T})&#39;
\hat R=(X&#39;X)^{-1}X&#39;Y
\hat \sigma_{\rho}= (s_{t} e_{i}&#39;(X&#39;X)^{-1} e_{i})^{\frac{1}{2}}
其中： e_{i}=[0,...,0,1]&#39;=(e)_{(p+2) \times 1}
s_{t}=\frac{1}{T-2p-2}(Y-\hat Y)&#39;(Y-\hat Y)，\hat Y =X\hat R

（3）PP检验统计量的计算
PP检验优化的是DF统计量，通过非参数方法来修正DF统计量，使其具有滞后期估计功能
对于（1）中三种情况计算的DF统计量t，PP检验统计量如下计算：
首先令
u=Y-\hat Y
其中 \hat Y 为（1）中对应三种情况计算  的 估计值，显然u为一个长度为T-1的向量
然后计算各阶滞后期下的残差自协方差估计
\gamma_{q}=\frac{1}{T-1}\Sigma_{t=q+1}^{T-1}u_{t}u_{t-q}
如下计算Newey-West估计量
\lambda^2(q) =\gamma_{0}+2\Sigma_{j=1}^{q}(1-\frac{j}{q+1})\gamma_{j}
PP检验统计量为:
\tau=\sqrt\frac{\gamma_{0}}{\lambda^{2}(q)}\ t+ [\frac{\lambda^{2}(q)-\gamma_{0}}{2(\lambda^{2}(q))^{\frac{1}{2}}}] \frac{(T-1)\hat\sigma_{\rho}}{MSE}  
t和 \hat\sigma_{p} 同样分（1）的三种情况计算
对应（1）中三种情况的  MSE分别计算如下
MSE=\frac{1}{T-2}u&#39;u (情况①）
MSE=\frac{1}{T-3}u&#39;u (情况②）
MSE=\frac{1}{T-4}u&#39;u (情况③）

对应的ADF和PP检验计算结果  如下，和SAS计算结果一致








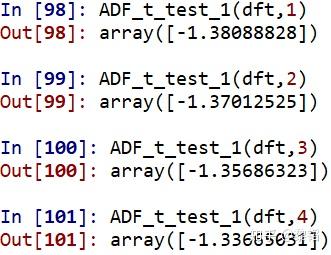
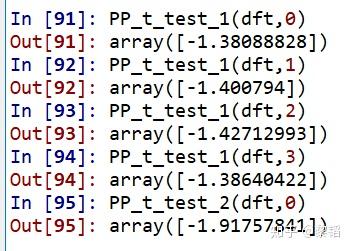
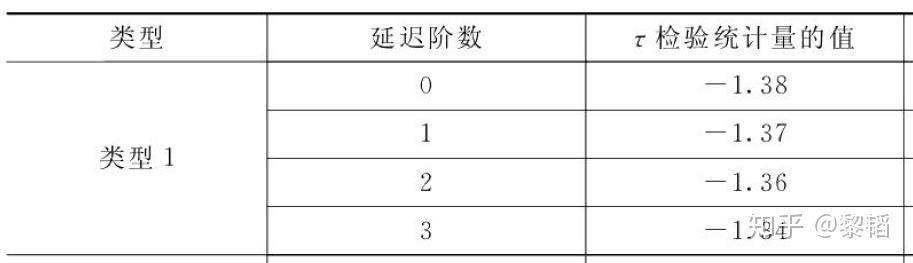
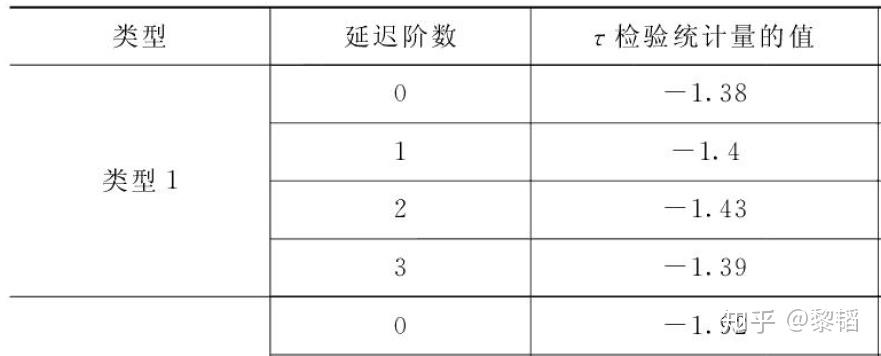
(测试数据来源：王燕《应用时间序列分析》(第四版)P229-233)

原文地址：https://zhuanlan.zhihu.com/p/40017350