金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
登陆有奖并可浏览互动!
您需要 登录 才可以下载或查看,没有账号?立即注册


×
一、Z检验统计量Z检验也称u检验。在原假设成立时,检验统计量服从标准正态分布,故称z检验。1、单个正态总体均值的检验设x1,x2,…xm是来自正态总体N(μ,δ2)的样本,在总体方差已知的情况下,如果需要对总体的均值进行检验,就可以假设H0: μ=μ0,H1: μ≠μ0,此检验可以使用的检验统计量为
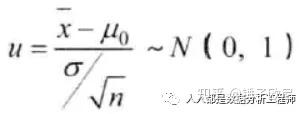
例如,一个由50名学生组成的样本其平均身高为174.94cm,标准差为6.42cm,假设样本是抽自平均身高为172.50m的总体,这样样本的值与总体均值间的误差(X—-μ)=174.94-172.50=24m,问这一误差是否属于抽样误差?假定显著性水平为0.05。解:1)、陈述假设:H0: μ1=μ2,H1: μ1≠μ22)、识别检验统计量并计算

3)、规定显著性水平:α=0.05。
4)、双侧检验如果Z>Z1-α/2=1.96,则拒绝零假设。5)、因为Z=2.68>Z1-α/2。=1.96,所以应拒绝零假设。这就是说,在0.05显著性水平下,由平均身高174.94cm的50名学生所组成的样本,不是抽自平均身高为172.50cm的总体,也就是所观察到的两者的误差,不是抽样误差。2、两个正态总体均值之差的检验设x1,x2,…xm是来自正态总体N(μ1,δ21)的样本,y1,y2,…yn是来自于另一个正态总体N(μ1,δ22)的样本,在两个总体方差已知的情况下对总体均值之差的检验。如果H0: μ1-μ2 = 0,H1: μ1-μ1≠0。检验的统计量为:
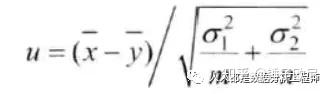
例:有两种方法可以用于制造某种以抗拉强度为重要特征的产品。以往经验表明,用这两种方法生产出来的产品,其抗拉强度都近似服从正态分布。方法1给出的标准差为6磅,方法2给出的标准差为8磅,工厂管理部门想知道这两种方法所生产出来的产品的平均抗拉强度是否不同?1)、陈述假设:H0: μ1-μ2 = 0,H1: μ1-μ1≠02)、检验统计量及其计算:
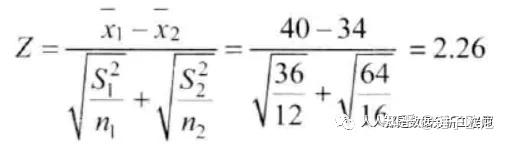
3)、指定显著性水平:α=0.05。4)、如果检验统计量的计算值大于或等于+1.96,或者小于或等于-1.96,就否定H0。5)、判断:因为2.26>1.96,所以否定H0由此可知,在样本数据的基础上,得出这两个总体平均值不相同的结论,即就平均来说,这两种方法不能生产出抗拉强度相同的产品。二、t检验统计量在原假设成立时,检验统计量服从t分布,故称t检验。1、单个正态总体在方差未知的情况下总体均值的检验。如果H0: μ=μ0,H1: μ≠μ0检验统计量为:
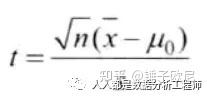
2、两个正态总体均值之差的检验设x1,x2,…xm是来自正态总体N(μ1,δ21)的样本,y1,y2,…yn是来自于另一个正态总体N(μ1,δ22)的样本,在两个总体方差未知的情况下,δ21=δ22=δ2,μ1-μ2的检验。如果H0: μ1-μ2 = 0,H1: μ1-μ1≠0。检验的统计量为:

其中,
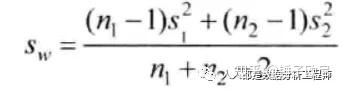
例:设两个由10人组成的样本,其身高均值分别为176.60cm与173.60cm,标准差分别为5.38cm与5.62cm。问这两个样本是否抽自同一总体,显著性水平为0.05解:1)、陈述假设:H0: μ1-μ2 = 0,H1: μ1-μ1≠0。2)、显著性水平:α=0.05。3)、将题中相应数代入统计量计算式:

4)、临界值: t0.05(10+10-2)=2.101。
5)、判断:t=1.22<t0.05=2.101,因而不能拒绝零假设,即认为这两个样本可能来自同一总体。
三、χ2检验统计量在原假设成立时,检验统计量服从χ2分布,故称χ2检验。设x1,x2,…xn是来自正态总体N(μ,δ2)的样本,对其方差的检验。检验的统计量为:
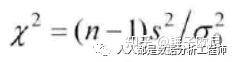
例:某类钢板的制造规格规定,“钢板重量的方差不超过0.016磅”。由25块钢板组成的一个随机样本,给出的方差为0.025。从这些数据能否得出钢板不合适的结论?解:1、陈述假设:H0:σ2<=0.016, H1:σ2>0.016。2、显著性水平:α=0.05。3、检验统计量:
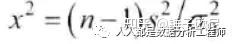
4、尺度:对于α=0.05和自由度为24,χ2的临界值为36.415。如果χ2的计算值大于或等于36.415,就否定H0。5、计算样本统计量的值:
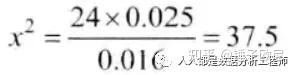
6、判断,因为37.5>36.415,应否定H0。分析结论为钢板的方差不合规格。
四、F检验统计量在原假设成立时,检验统计量服从F分布,故称F检验。设x1,x2,…xm是来自正态总体(μ1,δ21)的样本,y1,y2,…ym来自于另一个正态总体N(μ1,δ22)的样本,对两个总体方差的检验。如H0:σ21=σ22,H1:σ21≠σ22。检验的统计量为:
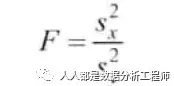
F检验的例子在后续课程中给出。五、各种检验统计量一览表
1、单个正态总体的均值与方差的假设检验设总体N(μ,δ2),给定量著性水平α。X1, X2, …, Xn为来自总体X的样本,
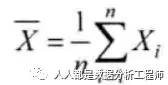
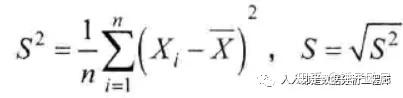
关于总体均值μ与方差δ2的假设检验,见下表
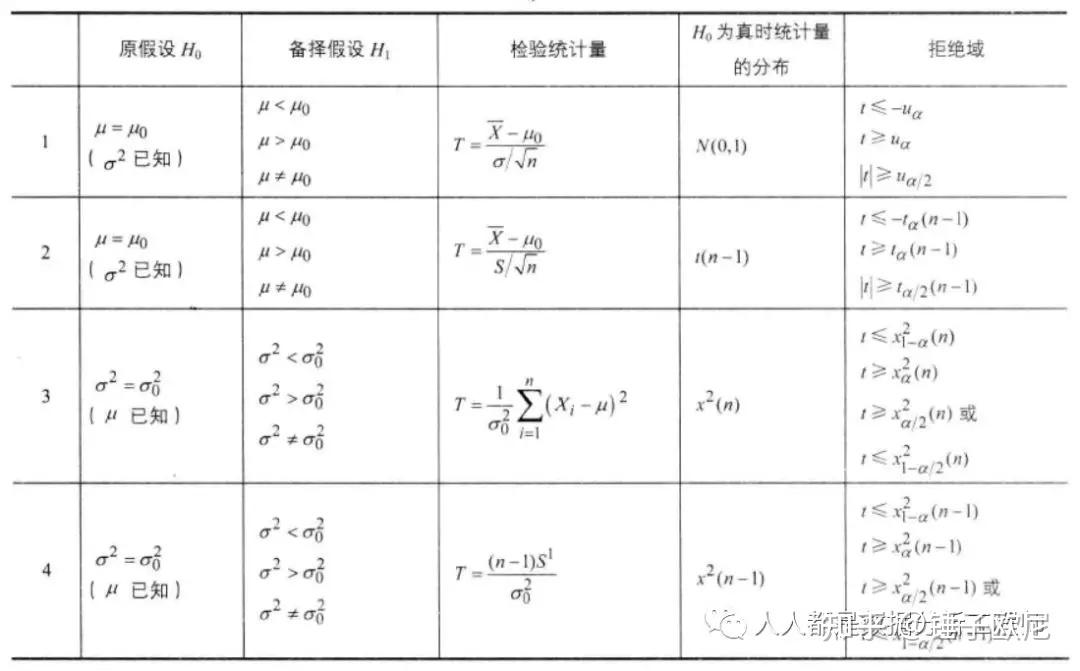
2、两个正态总体的均值与方差比的假设检验设有两个正态总体X~N(μ1,δ21), Y~N(μ2,δ22)X1, X2, …, Xn1 与 Y1, Y2, …,Yn2且X与Y相互独立。分别来自总体X与Y的两个互相独立的样本。
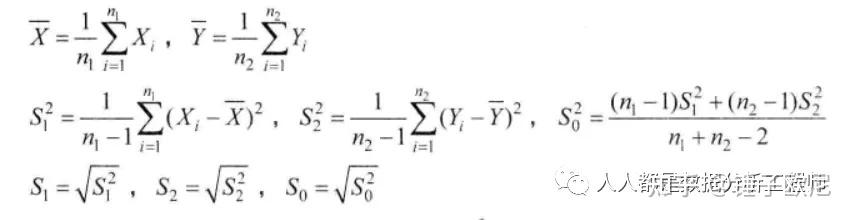
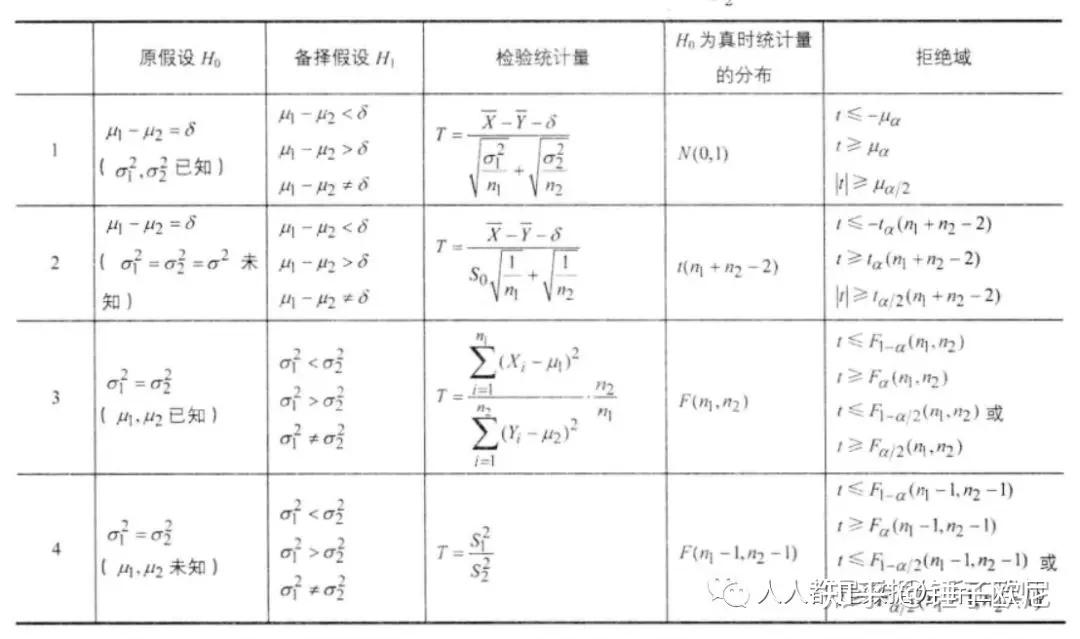
原文地址:https://zhuanlan.zhihu.com/p/423765543 |
|
 /3
/3 