车辆侧向运动学和动力学模型

HaHa

刚刚开始学习做自动驾驶路径规划，前辈推荐我先去了解汽车的结构，最近看到《车辆动力学及其控制》这本书上对车辆的运动学和动力学模型讲解非常到位。打算分享一下其中的内容，并对它省略的一些过程进行补充推导。
最近越来越感觉到对初学者来说数学真是一切的基石，虽然现在已经有各种各样的库，不用自己搞清楚具体是怎么算的，但是对于一名算法工程师我觉得还是很有必要去了解底层的数学原理。
首先区分一下的运动学模型（Kinetic Model）和动力学模型（Dynamic Model），这两个模型在刚听到的时候一直不了解其中的区别是什么。

• 运动学模型使用几何方法研究物体运动，只考虑物体的形状和运动关节，不考虑物体的质量和相互作用力，主要研究点和刚体的运动。
  
• 动力学模型研究力与运动的关系，以牛顿第二定律 F=ma 为核心，分析力、质量与加速度的关系。
  

直观地理解，运动学模型关注物体的位置和姿态，动力学模型关注物体的加速度、角速度。
单车模型

要控制车辆运动，首先需要对车辆建立数学模型，反映车辆的真实特性，并且模型尽可能的简单实用。自行车模型是一种常见的车辆运动学模型，如图1所示，单车模型主要是以下几个假设：

• 假设忽略车辆在垂直方向的运动，只考虑车辆在 XOY 平面下的运动，车辆是一个二维平面上的运动物体；
  
• 假设车辆的两个前轮有一样的转动角度和速度等，两个后轮同样如此，前后的轮胎可以各用一个轮胎来描述；
  
• 假设车辆运动和自行车一样，前轮控制转角，后轮提供运动速度；
  
• 车身及悬架系统是刚性的。
  

要重视假设部分，了解模型的研究范围，后续复杂的研究很多都是在强假设的基础下，一步步弱化假设条件。了解了模型的研究范围，至少能够知道在研究一个什么东西。
车辆侧向运动学和动力学模型的代码实现：
车辆侧向运动学模型推导

研究运动学模型，首先需要对车辆模型进行一定的假设：

• 车辆满足单车模型的假设；
  
• 假设车辆在低速情况下运行，车轮没有侧偏，车轮的速度方向就是车轮的转向角方向。
  

运动学模型，主要是研究车辆在低速的情况下的运动状态。低速状态下的车辆有一个非常好的性质，车轮没有侧偏，即车轮的速度矢量方向车轮转动的方向一致，即车轮转向角 \delta_f 和 \delta_r 表示的方向。
车轮的侧偏（可参考图3），是在车辆高速运动的情况下，轮胎与地面接触的地方扭曲了，轮胎实际受力的方向跟车辆转向机构转动的角度不一致。可以参考这个视频（车轮侧偏现象）1分20秒开始的现象，这时车轮的速度矢量方向和车轮的转动方向不一致。



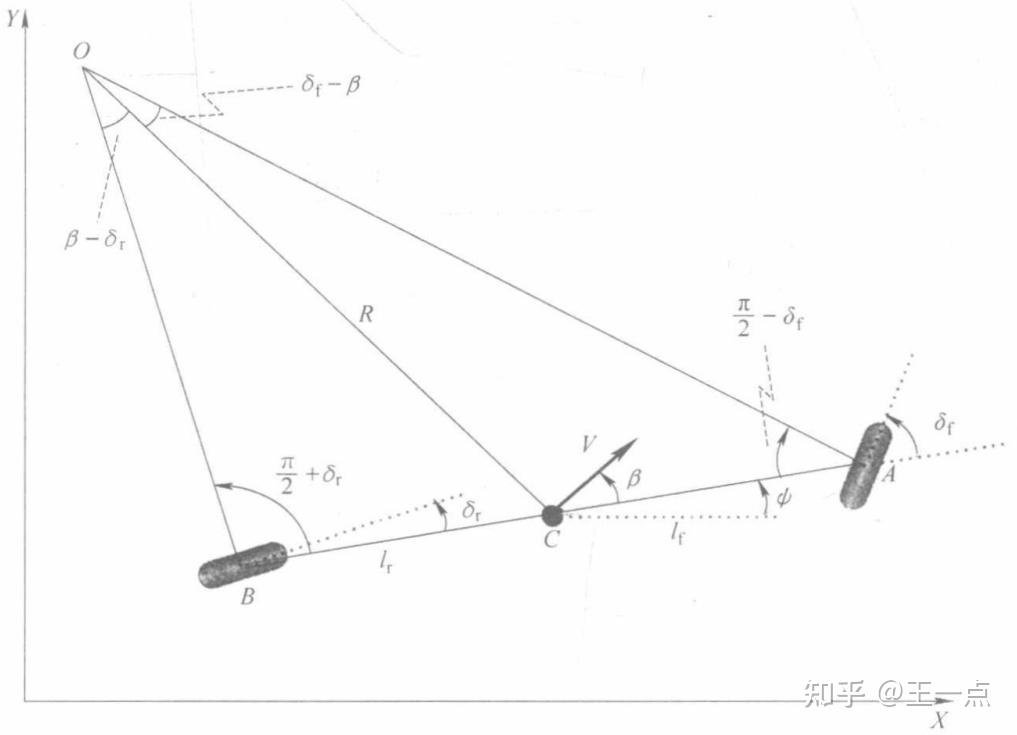
图1 车辆侧向运动学模型（图片来源：《车辆动力学及其控制》）

图中， A 、 B 、 C 分别表示车辆模型前轮、后轮和质心的位置；车辆质心到点 A 和到点 B 的距离分别为 l_f 和 l_r ，车辆的轴距 L=l_f + l_r ； \delta_f 和 \delta_r 分别表示前轮转角和后轮转角（实际情况中后轮转角一般为 0 ，书里为了理论的完整性引入了后轮转角）； R 表示车辆的转弯半径； V 表示车辆质心处的速度，表示车辆实际运动的速度； \beta 表示车辆的侧偏角，是车辆质心速度与车辆纵轴，即 AB ，之间的夹角； \psi 为车辆的横摆角，是车辆纵轴与世界坐标系之间的夹角，世界坐标系可以理解为最大的、不变的坐标系；车辆方向角（航向角、偏航角）为 \gamma = \beta + \psi 。图中有一些角度可以根据几何关系自行推导一下。
先给出最终需要求的车辆的侧向运动学模型（书中的模型是用质心来分析的，也可以用后轮中心来分析）：
     \left\{     \begin{aligned}         &\dot{x} = v\cos(\beta + \psi) \\         &\dot{y} = v\sin(\beta + \psi) \\         &\dot{\psi} = \frac{v}{L}\cos(\beta)\left(\tan(\delta_f) - \tan(\delta_r)\right) \\     \end{aligned}     \right. \tag{1}  
这是最终需要求解的模型，运动学模型是用 \dot{x}, \dot{y}, \dot{\psi} 三个物理量来描述车辆模型的运动状态。主要分析点和刚体的运动，不涉及物体受力情况。其中 \dot{x}, \dot{y} 就是速度在世界坐标系下 x, y 方向上的分量， \dot{\psi} 为车辆的横摆角速率。
其中的 \dot{x}, \dot{y} 比较好求，就是速度的分量，不展开分析。主要分析角速率 \dot{\psi} 的计算，用 v, L, \delta_f, \delta_r, \beta 这几个已知或比较容易测量的量来描述。
角速率 \dot{\psi} 的计算可以套用圆周运动角速度和线速度的公式 v = \dot{\psi} R 。
     \dot{\psi} = \frac{v}{R} \tag{2} 其中转弯半径$R$可以用两次正弦定理来计算：
    \left\{         \begin{aligned}             &\frac{OB}{\sin(\angle{OAB})} = \frac{AB}{\sin(\angle{AOB})} \\             &\frac{OB}{\sin(\angle{OCB})} = \frac{OC}{\sin(\angle{OBC})}     \end{aligned}     \right. \tag{3}
     R = OC = AB\frac{\sin(\angle{OAB})}{\sin(\angle{AOB})}\frac{\sin(\angle{OBC})}{\sin(\angle{OCB})} = L \frac{\cos(\delta_f)}{\sin(\delta_f - \delta_r)}\frac{\cos(\delta_r)}{\cos(\beta)} \tag{4}  
最后把式(4)代入式(2)就能得到车辆模型横摆角速度的表达式，至此完成车辆动力学模型的推导。
     \dot{\psi} = \frac{v}{R} = \frac{v}{L} \cos(\beta) (\tan(\delta_f) - \tan(\delta_r)) \tag{5}
车辆侧向动力学模型推导

侧向动力学模型，是车轮没有侧偏的假设不成立的情况，车在高速行驶时车轮存在侧偏，但同样是基于单车模型。书里为了推导简单，在推导动力学模型时就没考虑后轮转角（我觉得前面考虑了后轮转向角，后面又没考虑，有点混乱，但还是跟着书来），只用 \delta 表示前轮的转向角。



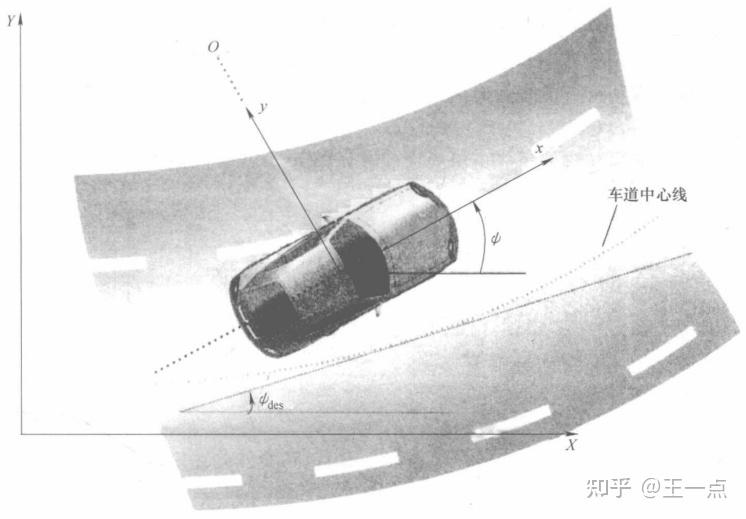
图2 车辆侧向动力学（图片来源：《车辆动力学及其控制》）



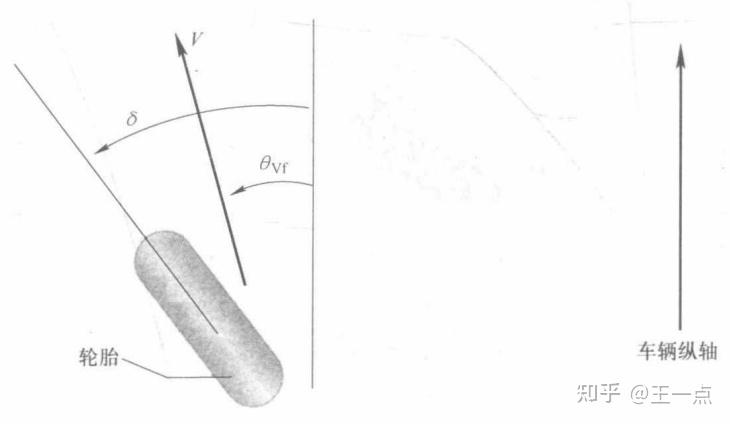
图3 轮胎侧偏角示意图（图片来源：《车辆动力学及其控制》）

如图2所示，考虑二自由度车辆，两自由度用车辆侧向位置 y 和车辆方向角 \psi 表示；车辆的侧向位置可沿车辆横向轴到车辆旋转中心点 O 测量得到，车辆方向角 \psi 由与系统 X 轴的夹角测得；车辆在质心处纵向速度用 v_x 表示。图3中 \delta 表示前轮的转向角， \theta_{Vf} 表示前轮的速度角， V 表示前轮的运动方向。
先给出最终要求的车辆的侧向动力学模型，因为比较复杂，所以给了状态空间方程，系统状态为 [y, \dot{y}, \psi, \dot{\psi}]^T ，控制输入为前轮转向角 \delta ：
     \begin{bmatrix}         \dot{y}     \\         \ddot{y}    \\         \dot{\psi}  \\         \ddot{\psi} \\     \end{bmatrix}     =     \begin{bmatrix}         0 & 1                                            & 0       & 0                                                         \\         0 & -\frac{2C_{\alpha f} + 2C_{\alpha r}}{m v_x} & 0       & -(v_x + \frac{2C_{\alpha f}l_f - 2C_{\alpha r}l_r}{m v_x}) \\         0 & 0                                            & 0       & 1                                                         \\         0 & -\frac{2l_r C_{\alpha f} - 2l_r C_{\alpha r}}{I_z v_x} & 0 & -\frac{2l_f^2 C_{\alpha f} + 2l_r^2 C_{\alpha r}}{I_z v_x}     \end{bmatrix}     \begin{bmatrix}         y          \\         \dot{y}    \\         \psi       \\         \dot{\psi} \\     \end{bmatrix}     +     \begin{bmatrix}         0                             \\         \frac{2C_{\alpha f}}{m}       \\         0                             \\         \frac{2l_f C_{\alpha f}}{I_z}     \end{bmatrix}     \delta     \tag{6}  
首先要对车辆进行受力分析，在忽略空气作用的情况下，车辆只受到地面的作用力 F 。因为这里只讨论车辆的侧向模型，所以用 F_y 表示车辆受到的侧向力，车辆侧向力由前轮侧向力 F_{yf} 和后轮侧向力 F_{yr} 组成。
     F_y = F_{yf}+F_{yr} = m a_y \tag{7}  
式中， m 表示车辆质量， a_y 表示车辆侧向加速度。车辆侧向的平动包括沿 y 方向的平移和绕点 O 的旋转两项，都是在侧向力 F_y 的作用下实现。沿 y 方向平移的加速度为 \ddot{y} ，绕点 O 旋转的向心加速度套用圆周运动公式为 \dot{\psi} v_x ，因此侧向加速度 a_y 为：
     a_y = \ddot{y} + \dot{\psi} v_x \tag{8}  
把式(8)代入式(7)可以得到第一条车辆侧向运动方程：
     m(\ddot{y} + \dot{\psi}v_x) = F_{yf} + F_{yr}\\ \tag{9}  车辆除了平动，还存在绕自身质心旋转的情况，这里套用转矩平衡方程，可以直接得到第二条车辆侧向运动方程：     I_z\ddot{\psi} = l_f F_{yf} - l_r F_{yr} \tag{10}式中， I_z 表示车辆的转动惯量， l_f 和 l_r 分别表示车辆质心到前轴和后轴的距离， \ddot{\psi} 表示车辆方向角的角加速度。
\left\{ \begin{aligned}     &m(\ddot{y} + \dot{\psi}v_x) = F_{yf} + F_{yr}\\     &I_z\ddot{\psi} = l_f F_{yf} - l_r F_{yr} \end{aligned} \right. \tag{11}  
接下来是对车辆的轮胎进行建模，如图3所示，分析轮胎侧向力 F_{yf} 和 F_{yr} 。试验结果表明当轮胎侧偏角较小时，轮胎侧向力与侧偏角成正比（具体可以看《车辆动力学及其控制》第13.4节）。这里直接给出结果，前轮和后轮的侧偏力为：
    \left\{     \begin{aligned}         &F_{yf} = 2C_{\alpha f}\alpha_f\\         &F_{yr} = 2C_{\alpha r}\alpha_r     \end{aligned}     \right. \tag{12}  
式中， \alpha_f = \delta - \theta_{v_f} 为前轮的侧偏角， \alpha_r = -\theta_{v_r} 为后轮的侧偏角， \theta_{v_f} 和 \theta_{v_r} 分别为前后轮的速度角，表示前后轮的速度方向， C_{\alpha f} 和 C_{\alpha r} 分别表示前后轮的侧偏刚度。侧偏刚度与轮胎的性质有关，可以通过实验测量得到。
关于前后轮速度角的计算，书里面没给出详细的说明，网上看到一个非常好的解释：



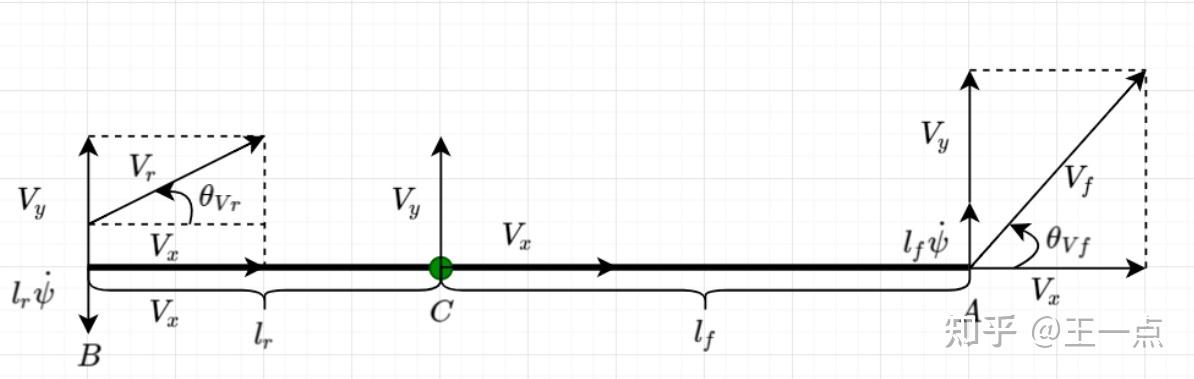
图4 车轮速度角计算示意图（图片来源：网络）

车辆的运动由平动和绕C点旋转组成，平动产生 v_x 、 v_y 两个速度分量，其中 v_y 用 \dot{y} 表示，旋转产生 l_f \dot{\psi} 、 l_r \dot{\psi} 两个线速度。根据几何关系可以计算速度角：
     \left\{     \begin{aligned}         &\tan(\theta_{v_f}) = \frac{\dot{y} + l_f \dot{\psi}}{v_x}\\         &\tan(\theta_{v_r}) = \frac{\dot{y} - l_r \dot{\psi}}{v_x}     \end{aligned}     \right. \tag{13}  
通常情况下速度角很小，用小角度近似原理得：
     \left\{     \begin{aligned}         &\theta_{v_f} = \frac{\dot{y} + l_f \dot{\psi}}{v_x}\\         &\theta_{v_r} = \frac{\dot{y} - l_r \dot{\psi}}{v_x}     \end{aligned}     \right. \tag{14}  
把式(14)代入式(12)，再把式(12)代入式(11)，可以得到式(15)和式(17)，分别计算状态量 \ddot{y} 和 \ddot{\psi} 与系统状态 [y, \dot{y}, \psi, \dot{\psi}]^T 以及控制输入 \delta 的关系，具体过程如式(16)和式(17)所示。
\ddot{y} + \dot{\psi}v_x = \frac{2C_{\alpha f}}{m}(\delta - \frac{\dot{y} + l_f \dot{\psi}}{v_x}) - \frac{2C_{\alpha r}}{m}\frac{\dot{y} - l_r \dot{\psi}}{v_x} \tag{15}  
     \begin{aligned}         \ddot{y} &= \frac{2C_{\alpha f}}{m}(\delta - \frac{\dot{y} + l_f \dot{\psi}}{v_x}) - \frac{2C_{\alpha r}}{m}\frac{\dot{y} - l_r \dot{\psi}}{v_x} - \dot{\psi}v_x \\         &= -\frac{2C_{\alpha f}\dot{y} + 2C_{\alpha f}l_f \dot{\psi} + 2C_{\alpha r}\dot{y} - 2C_{\alpha r}l_r \dot{\psi}}{m v_x} - \dot{\psi} v_x + \frac{2C_{\alpha f}}{m}\delta \\         &= -\left(\frac{2C_{\alpha f} + 2C_{\alpha r}}{m v_x}\dot{y} + \frac{2C_{\alpha f}l_f - 2C_{\alpha r}l_r}{m v_x}\dot{\psi}\right) - v_x \dot{\psi} + \frac{2C_{\alpha f}}{m}\delta \\         &= -\frac{2C_{\alpha f} + 2C_{\alpha r}}{m v_x}\dot{y} - \left(v_x + \frac{2C_{\alpha f}l_f - 2C_{\alpha r}l_r}{m v_x}\right)\dot{\psi} + \frac{2C_{\alpha f}}{m}\delta     \end{aligned} \tag{16}  
     I_z \ddot{\psi} = 2l_f C_{\alpha f}\left(\delta - \frac{\dot{y} + l_f \dot{\psi}}{v_x}\right) + 2l_r C_{\alpha r}\frac{\dot{y} - l_r \dot{\psi}}{v_x} \tag{17}
     \begin{aligned}         \ddot{\psi} &= \frac{2l_f C_{\alpha f}}{I_z}\left(\delta - \frac{\dot{y} + l_f \dot{\psi}}{v_x}\right) + \frac{2l_r C_{\alpha r}}{I_z}\frac{\dot{y} - l_r \dot{\psi}}{v_x} \\         &= -\frac{2l_f C_{\alpha f}}{I_z v_x}\dot{y} - \frac{2l_f^2 C_{\alpha f}}{I_z v_x}\dot{\psi} + \frac{2l_r C_{\alpha r}}{I_x v_x}\dot{y} -\frac{2l_r^2 C_{\alpha r}}{I_z v_x}\dot{\psi} + \frac{2l_f C_{\alpha f}}{I_z}\delta \\         &= -\frac{2l_f C_{\alpha f} - 2l_f C_{\alpha r}}{I_z v_x}\dot{y} - \frac{2l_f^2 C_{\alpha f} + 2l_r^2 C_{\alpha r}}{I_z v_x}\dot{\psi} + \frac{2l_f C_{\alpha f}}{I_z}\delta     \end{aligned} \tag{18}  
最后整理成矩阵的形式，得到车辆侧向动力学模型的状态空间方程。

原文地址：https://zhuanlan.zhihu.com/p/699299378