金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
登陆有奖并可浏览互动!
您需要 登录 才可以下载或查看,没有账号?立即注册


×
样本浓度的分析是根据标准品数据所生成的标准曲线完成的,要确保样本结果的准确性,就要保证标准曲线尽量能还原抗原抗体的动力学反应过程。
一般情况按照说明书推荐方法拟合标曲,可以用软件绘制也可以手动制作。标曲呈现s型曲线,两端趋于水平,中间趋于线性,中间部分为较佳的检测范围。当标准品的量超过与包被抗体结合的量,此时标准品已饱和,在增加标准品的量,其OD值不再变化,故当标准品达到一定浓度后,曲线趋于水平。按照科学分析方法,如果存在奇异点或者污点,直接采用线性分析不是很好,要对拟合曲线的几个点进行取舍,同时也可以改用双对数直线拟合或者四参数曲线拟合。
那么常用的曲线拟合回归方程主要为以下7种:
1.直线回归
直线回归是最简单的回归模型,也是最基本的曲线拟合回归分析方法,将所有的测试点拟合为一条直线。
其拟合函数方程式为:y=a+bx
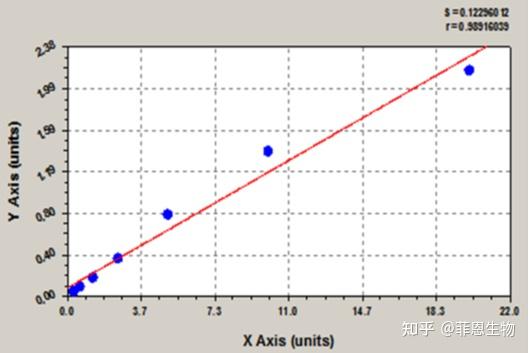
直线回归标曲
2.二次多项式拟合回归方程
二次多项式成抛物线状,开口向下或者向上,在很多ELISA实验中,拟合近似于二次多项式的升段或者降段,由于曲线的特性,同一个浓度值在曲线图上可能表现出没有对应的OD值、有一个OD值,或者两个OD值,所以使用二次多项式拟合时,最好保证取值的范围都落在曲线的升段或者降段,否则哪怕是相关系数很好也很可能与实际的值不一致。
其拟合函数方程式为:y = a + b x + c x2
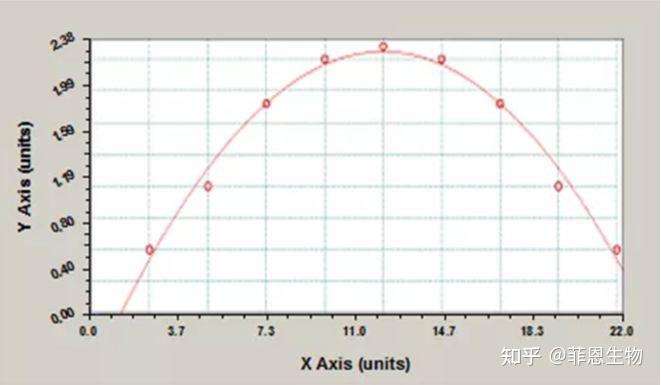
二次多项式拟合回归方程标曲
3.三次多项式拟合回归方程
三次多项式像倒状的‘S’形,在实验结果刚好在曲线的升段或者降段的时候,效果还可以,但是对于区间较广的情形, 由于其弯曲的波动,三次方程拟合模拟不一定很好.跟二次方程拟合一样,看曲线的相关系数的同时也要看计算的点在曲线上的分布,这样才算出理想的结果,本软件计算值时,选择性的取相对于浓度或者OD值,比较符合实际的那个结果,而没有将多个结果列出。
拟合函数方程式为:y = a + b x + c x2 + d x3
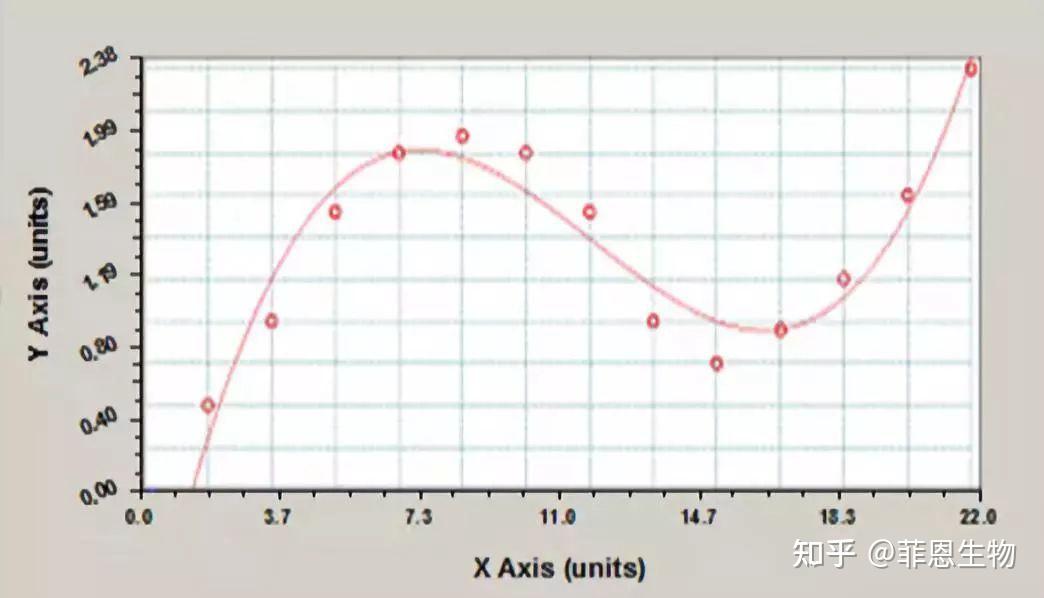
三次多项式拟合回归方程标曲
4.半对数拟合回归方程
半对数拟合即将浓度值取对数值,然后再和对应的OD值进行直线回归,理想的状态下,在半对数坐标中是一条直线,常用于浓度随着OD值的增加或者减低呈对数增加或者减少的情况,即浓度的变化比OD值的变化更为剧烈。在ELISA实验中较常用(有很多用EXCEL画图时,也常使用半对数)。
拟合函数方程式为:y = a lg(x) + b
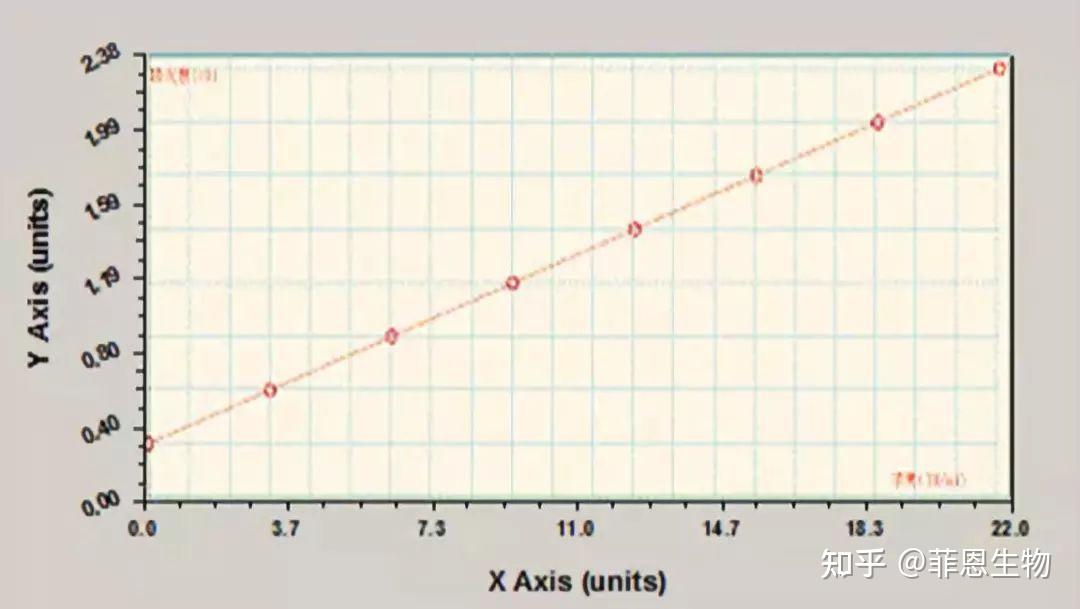
半对数拟合回归方程标曲
5.Log-Log拟合回归方程
Log-Log拟合和半对数相似,只是将OD值和对应的浓度值均取对数,然后再进行直线回归。
拟合函数方程式为:lg(y) = a lg(x) + b
Log-Log拟合回归方程标曲
6.Logit-Log拟合回归方程
Logit-log则是免疫学检测中的模型, 可用于竞争法。它最早用于 RIA,但在 ELISA 中也是可以应用的。Logit 变换源于数学中的 Logistic 曲线。在竞争法放射免疫分析(RIA) 及 ELISA 中,当竞争性反应物为 0 时结合率为 100%,如果某一浓度下结合率为 B,B=OD/OD(0),在对B进行 Logit 变换:y=ln[B/(1-B)],之后y与浓度的对数成线性关系,即:y = a + b lg(x),拟合函数方程式为:lg(y) = a lg(x) + b 就得到了Logit-log 直线回归模型,这个模型一般适用于竞争法的拟合,所以拟合时要求只有少有一个零浓度测试的OD值,并且此值为整个反应的最大值(也就是我们常说的至少要做一个空白对照)。
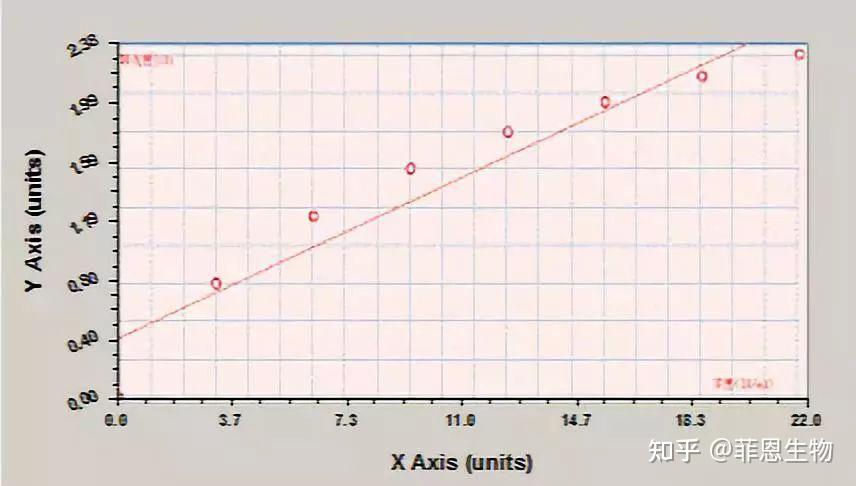
7.四参数拟合回归方程
竞争法和夹心法都可以用到。它的形状, 根据情况, 可能是一个单调上升的类似指数, 对数, 或双曲线的曲线, 也可能是一个单调下降的上述曲线, 还可以是一条 S 形曲线。它要求 X 值不能小于0 (因为指数是实数, 故有此要求)。在很多情况下它都可以拟合 ELISA 的反应曲线, 所以它也成了 ELISA 中应用最广的模型之一。
四参数方程的拟合函数表达式为:
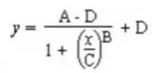
四参数方程的拟合函数
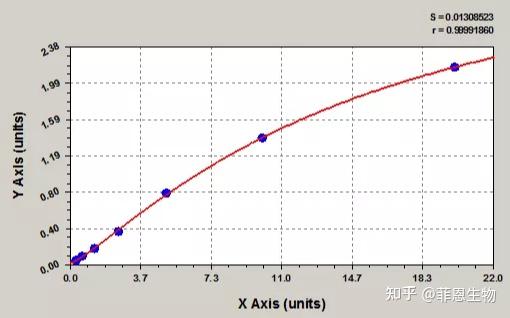
四参数拟合回归方程标曲
切记,在实验过程中,要根据各个实验本身的特点,选择最适合的曲线拟合模型,才能得到最合理的实验结果, 一般情况下,需要综合考虑标准曲线的趋势走向以及R值的大小,来最终选择适合自己的回归方程。
原文地址:https://zhuanlan.zhihu.com/p/666926729 |
|
 /3
/3 