傻傻分不清：时间趋势项与时间虚拟变量

临床医师 · 发表于 2024-11-3 21:58

登陆有奖并可浏览互动！

您需要登录才可以下载或查看，没有账号？立即注册

×

徐婷 (对外经贸大学), xt2544720640@foxmail.com
徐云娇 (厦门大学)，jilyo@stu.xmu.edu.cn

原文阅读：时间趋势项 v.s. 时间虚拟变量

Stata连享会主页 || 视频 || 推文

http://qr06.cn/B9EOq8 (二维码自动识别)
<hr/>Note: 助教招聘信息请进入「课程主页」查看。

因果推断-内生性专题 ⌚ 2020.11.12-15
主讲：王存同 (中央财经大学)；司继春(上海对外经贸大学)
课程主页：https://gitee.com/arlionn/YG | 微信版

http://qr32.cn/BlTL43 (二维码自动识别)

空间计量专题 ⌚ 2020.12.10-13
主讲：杨海生 (中山大学)；范巧 (兰州大学)
课程主页：https://gitee.com/arlionn/SP | 微信版

https://gitee.com/arlionn/DSGE (二维码自动识别)
<hr/>目录

<hr/>1. 时间趋势项与时间虚拟变量

1.1 时间趋势项

许多经济、金融时间序列会随时间有一个增长的趋势，我们称其具有时间趋势 (time trend)。假如在因果推断中我们忽视了两组序列具有相同或者相反的趋势，则很有可能错误地认为其中一个变量的变化是由另一个变量的变化所导致的，导致伪回归问题 (spurious regression problem)。
在回归方程中加入时间趋势项可以避免此问题，常见的时间趋势有线性趋势 (linear time trend)、指数趋势 (exponential trend) 与二次型趋势 (quadratic time trend)。
1.1.1 线性趋势

考虑以 y_t 作为被解释变量，有两个可观测解释变量 (x_{t1}, x_{t2}) 的线性回归方程：
y_{t}=\beta_{0}+\beta_{1}x_{t1}+\beta_{2}x_{t2}+\beta_{3}t+u_{t}  \tag{1}
系数 \beta_{3} 的含义是：其他变量不变的条件下，随时间流逝 y_{t} 从某一期到下一期所发生的变化，这种变化的大小固定为 \beta_{3} ，并且与 x_{t1}，x_{t2} 是无关的。假如回归中遗漏了变量 t ，那么我们将会得到有偏的 \beta_{1}，\beta_{2} 的估计值。值得注意的是，当 x_{t1} 和 x_{t2} 也存在时间趋势时，变量 t 的遗漏仍然会造成系数估计的偏误。
1.1.2 指数趋势

指数趋势是指时间序列每一期的增长率是相同的，具体回归模型可表示如下：
\log({y_t})=\beta_{0}+\beta_{1}\log(x_{t1})+\beta_{2}\log(x_{t2})+\beta_{3}t+u_{t}  \tag{2}
此时再来考察系数 \beta_{3} 的含义，仍然假设其他变量不发生变化，即当 \Delta x_{t1}, \Delta x_{t2}=0 以及 \Delta u_{t}=0 时：
\Delta\log({y_t})=\log({y_t})-\log({y_{t-1}})\approx(y_t-y_{t-1})/y_{t-1}=\beta_{3}  \tag{3}
由以上推导可以看出，\beta_{3} 代表的是 y_t 每期的增长率，并且其不随时间变化。
1.1.3 二次型趋势

另一种比较常用的时间趋势项形式为二次型，与上两种形式不同的是，二次型时间趋势会随时间发生变化，考虑以下回归模型：
y_{t}=\beta_{0}+\beta_{1}x_{t1}+\beta_{2}x_{t2}+\beta_{3}t+\beta_{4}t^2+u_{t}  \tag{4}
此时，假设其他变量不变，我们对 y_{t} 关于 t 求导数，得到时间对 y_{t} 的边际效应为 \beta_{3}+2\beta_{4}t，显然因变量 y_{t} 的时间趋势会随时间改变，此时我们可以借助于 margins 与 marginsplot 命令更直观地进行边际分析。详情请见 Stata因子变量：好用好用！ (微信版)。
这里需要注意的是，不是加入越多高次的时间趋势项就越好，因为当我们加入足够多的 t 的多项式时，任何一组时间序列都能很好地被刻画，但对于我们寻找哪些自变量会影响 y_{t} 没有什么帮助 (Wooldridge, 2016)。
1.2 时间虚拟变量

时间序列所具有时间趋势是可以定量度量的 (通过 t=1,2,3\ldots)，但也存在一些影响经济变量的因素无法定量度量，比如季节对某些产品 (如冷饮) 销售的影响，战争、金融危机对 GDP 的影响等。为了在模型中反映这些因素的影响，并提高模型的精度，我们需要引入时间虚拟变量 (time dummies)，根据这些因素的属性类型人工取值为 “0” 或 “1” (李子奈, 潘文卿, 2010)。
1.2.1 季节性虚拟变量

假如一组时间序列是季度或更高频的数据，那么其很可能含有季节性因素 (seasonality)，在进行进一步回归分析之前，我们有必要对数据进行季节性调整，可以选择的方法包括：回归法、移动平均比率法以及目前最权威的 X-12 方法 (陈强, 2014)。这里，我们介绍不对数据进行预处理，而引入月度 (或季度) 虚拟变量直接回归的方法：
\begin{aligned} y_{t}=&\beta_{0}+\delta_{1}feb_{t}+\delta_{2}mar_{t}+\delta_{3}apr_{t}+\ldots+\delta_{11}dec_{t} \\ &+\beta_{1}x_{t1}+\ldots+\beta_{k}x_{tk}+u_{t} \end{aligned} \tag{5}
其中，feb_{t}, mar_{t},\ldots, dec_{t} 是月度虚拟变量，当 t 为相应月份时取 1，否则为 0。以上模型中，一月份 (January) 为基准组，并且 \beta_{0} 为一月份的截距项。若在控制了 x_{tk} 后不存在季节性因素，那么 \delta_{1} 至 \delta_{11} 应全为 0，即无法通过 F 检验。
1.2.2 年份虚拟变量

如果我们收集的数据为年度数据，那么是否就不需要考虑时间虚拟变量了呢？
答案是否定的，我们有时仍需要引入时间虚拟变量，以反映某些冲击事件对特定年度经济数据的影响，比如 2008 年的全球金融危机导致这一年几乎每个国家的股市出现下跌，再如 2020 年的新冠疫情将导致全球经济萎缩 5.2% (世界银行半年度《全球经济展望》)。
年份虚拟变量设置的方法与季节性虚拟变量设置的方法十分类似，同样也是在回归模型中引入一系列代表特定年份的虚拟变量：
y_{t}=\beta_{0}+\sum_{j=1}^{T-1} \tau_{j} T_{j}+\beta_{1}x_{t1}+\ldots+\beta_{k}x_{tk}+u_{t}  \tag{6}
如以上公式所示，\tau_{j} 是年份虚拟变量 T_{j} 的系数，若观测值在 j 年，T_{j} 等于1，否则为 0。一般而言，当数据集中包含 T 期时，应该加入 T-1 个年份虚拟变量。
1.3 二者的区别

在程序语句上，时间趋势项在 Stata 因子分析中被标示为连续变量，运算符为 c.x，如 c.year；而时间虚拟变量在 Stata 因子分析中被标示为类别变量，运算符为 i.x，如 i.year。
在经济含义上，时间趋势项通常近似代表了社会中所发生的技术进步；而时间虚拟变量的目的是控制住某些特殊年份造成的影响，例如严重的自然灾害、战争以及金融危机，参见 ResearchGate Question: Is anyone familiar with Time Trends vs Time Dummies?
在适用范围上，时间虚拟变量因其所受约束更少所以应用更加广泛。当把时间趋势项纳入模型时，实际上我们隐含假设了某些单调性 (线性趋势) 或某种函数形式；但是时间虚拟变量则不受此约束，它可以表现为毫无规律的 “锯齿” 形态，也可以表现为时间趋势项那样的函数形式。在某种程度上，时间虚拟变量可以吸收掉所有的特定时间效应，包括时间趋势，参见 Economics Job Market Rumors 。
总结以上，时间趋势项相当于赋予了给定年份一个时间指数（如果样本区间是 2000-2010 年，则时间趋势变量给 2000 年赋值为 1，2001 年赋值为 2 等），它可以解释其他自变量解释不了的因变量的外生增加或下降。时间虚拟变量则是当观测值在指定的月份/季度/年份时等于 1，否则等于 0，它控制住了特定时间的固定效应，比如指定时间段的冲击影响。
当然，假如有明确的需要以及可靠的理论依据，那么模型就可以同时纳入时间趋势项与时间虚拟变量。
2. Stata 范例

下面本文基于数据集 gss.dta 来简要说明在模型中加入时间趋势项和时间虚拟变量的区别和联系。degree 为因变量，表示被调查者的受教育程度；coh 为时间趋势项，用被调查者出生的年份减 1900 后除以10来衡量；year 为时间虚拟变量，用被调查者出生的年份减 1900 后设置的虚拟变量来衡量。
.use "http://fmwww.bc.edu/repec/bocode/g/gss.dta", clear
.gen year = coh*102.1 加入时间趋势项

在这里，我们在模型一中同时加入时间虚拟变量i.year、时间趋势项c.coh，在模型二中仅加入时间虚拟变量。回归后分别求取拟合值 yhat1 和 yhat2 ，通过比较两种拟合值的差异来分析两个模型的异同。
.reg degree i.year c.coh
.predict yhat1
.reg degree i.year
.predict yhat2
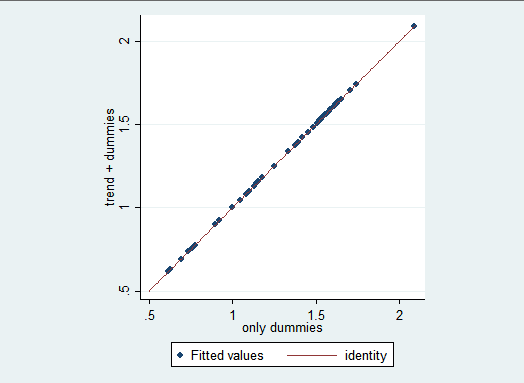
.twoway scatter yhat1 yhat2, aspect(1) || ///
      function identity = x, range(.5 2.1) ///
      ytitle(trend + dummies)             ///
      xtitle(only dummies)如下图所示，在包含时间虚拟变量的模型中加入时间趋势项后，并没有改变模型，只是将相同的信息以不同的系数进行区分。在本例中，两种模型得出的拟合结果是完全相同的。所以，如果在模型中同时加入时间虚拟变量和趋势项难以解释，在没有损失信息的情况下，可以去掉时间趋势项。

3.2 改变划分时间虚拟变量的时间跨度

在这里，我们将时间虚拟变量以每 10 年为单位进行划分，在模型三中同时加入以每 10 年为单位的时间虚拟变量i.decade、时间趋势项c.coh，在模型四中仅加入时间趋势项。回归后分别求取拟合值 yhat3 和 yhat4 ，再加上模型二的拟合值 yhat2 ，通过比较三个拟合值的差异来分析模型的异同。
.gen decade = floor(coh)
.reg degree i.decade coh
.predict yhat3
.reg degree coh
.predict yhat4
.sort coh
.by coh : gen byte mark = _n == 1
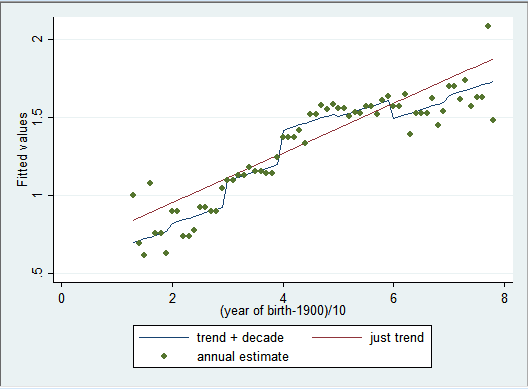
.twoway line yhat3 coh if mark ||          ///
      line yhat4 coh if mark ||          ///
      scatter yhat2 coh if mark,          ///
      legend(order( 1 "trend + decade"    ///
                  2 "just trend"       ///
                  3 "annual estimate" ))如果划分时间虚拟变量的时间跨度更长，例如，时间趋势项按年度划分，而时间虚拟变量按 10 年划分，那么这两个模型实质上是不同的。

3. 拓展：DID 中加入时间趋势项

3.1 理论基础

本部分以政策评估中常用的双重差分 (Differences in Diffenrences, DID) 模型为例：
\mathbf{Y}_{ist}=\gamma_{s}+\lambda_{t}+\delta\mathbf{D}_{st}+\mathbf{X}_{ist}^{\prime}\beta+\varepsilon_{ist} \tag{7}
其中，i 代表个体 (或公司)，s 代表各州 (或省份)，t 代表年份。\mathbf{Y}_{ist} 是 s 州的 i 个体在第 t 期的因变量 (受教育年限、工资等) 的观测值；\gamma_s 代表了州的固定效应；\lambda_t 为年份虚拟变量，代表了时间固定效应；\mathbf{D}_{st} 是政策实施与否的虚拟变量 (若 s 州在 t 期政策有实行，那么取值为1 ，否则为 0)，系数 \delta 代表了我们最为关心的政策效应。
在关于 DID 识别策略的稳健性检验中，我们必须验证干预组与控制组是否满足共同趋势假设，即在控制可观测协变量 \mathbf{X}_{ist} 后，干预组个体如果没有接受干预，其结果的变动趋势将与控制组的变动趋势是相同的。参见赵西亮 (2017)。
那么在共同趋势无法得到满足的情况下，我们该如何寻求解决方案呢？
三重差分 (DDD) 与合成控制法 (SCM) 固然是很好的解决办法，但在某些情况下，我们有更简便的选择，那就是往以上模型中加入时间趋势项，得到：
\mathbf{Y}_{i s t}=\gamma_{0 s}+\gamma_{1 s}t+\lambda_{t}+\delta\mathbf{D}_{st}+\mathbf X_{ist}^{\prime} \beta+\varepsilon_{ist} \tag{8}
Angrist & Pischke (2008) 指出，在各州具有不同 (但较有规律) 的变动趋势时，以上既包含了年份虚拟变量有包含了时间趋势项的 DID 模型，仍然可以对政策效应进行有效识别。原因是年份虚拟变量吸收了每个州时间上所受的共同冲击，时间趋势项又可以解决各州趋势不一致的问题。
3.2 Stata 实例

此部分参考先前推文：连享会-倍分法DID详解 (一)：传统 DID (微信版) 中的数据生成方法，改变干预组与控制组的时间趋势，并比较在未加入时间趋势项和加入时间趋势项的两种情况下，DID 模型是否可以正确估计政策效应。
3.2.1 数据生成过程

///设定60个个体，设定随机数种子
clear all
set obs 60
set seed 10101
gen id =_n

///生成有600个观测值的面板数据
expand 11
drop in 1/60
count

///生成州变量
gen State = 0
replace State = (inrange(id,31,60))

///以id分组生成时间标识
bys id: gen time = _n+1999

///生成协变量x1, x2

gen x1 = rnormal(1,7)
gen x2 = rnormal(2,5)

///生成treat和post变量，以2005年为接受政策干预的时点，id为31-60的个体为干预组，其余为控制组
gen D = 0
replace D = (inrange(id,31,60))
gen post = 0
replace post = (time >= 2005)

///生成时间变量
sort id time
by id: gen T = _n

///干预组与控制组的时间趋势不一致，政策的真实效果为10，且不随时间发生变化。
bys id: gen    y0 = 10 + 0.5 * T +    5 * x1 + 3 * x2 + rnormal()
bys id: gen    y1 = 15 +    T +    5 * x1 + 3 * x2 + rnormal() if time <  2005
bys id: replace y1 = 15 +    T + 10 + 5 * x1 + 3 * x2 + rnormal() if time >= 2005
gen y = y0 + D * (y1 - y0)

///将基础数据结构保存成dta文件
save "DID_Time_Trend.dta"，replace3.2.2 未加入时间趋势项

我们对 (7) 式模型进行实现：
///实现(7)式模型
clear
use "DID_Time_Trend.dta"
reg y i.State i.time c.D#c.post x1 x2, rStata 估计结果如下：
------------------------------------------------------------------------------
         |             Robust
         y |    Coef. Std. Err.    t P>|t|    [95% Conf. Interval]
-------------+----------------------------------------------------------------
   1.State | 6.541262 .1292255 50.62 0.000    6.287461 6.795064
         |
      time |
   2001  | .5158501 .2095098    2.46 0.014    .1043685 .9273316
   2002  | 1.470104 .2170314    6.77 0.000    1.04385 1.896358
   2003  | 2.054685 .2101834    9.78 0.000    1.641881    2.46749
   2004  | 2.728637 .2282535 11.95 0.000    2.280343 3.176932
   2005  | 2.325115 .2455191    9.47 0.000    1.842911    2.80732
   2006  | 2.956873 .2151182 13.75 0.000    2.534376 3.379369
   2007  | 4.080774 .221301 18.44 0.000    3.646134 4.515414
   2008  | 4.69696 .2323645 20.21 0.000    4.240592 5.153329
   2009  | 5.573186 .2389316 23.33 0.000    5.103919 6.042452
         |
  c.D#c.post | 12.37039 .178694 69.23 0.000    12.01943 12.72135
         |
      x1 | 4.99772 .0062709 796.97 0.000    4.985404 5.010037
      x2 | 3.005184 .0087694 342.69 0.000    2.987961 3.022408
   _cons | 10.17657 .1737664 58.56 0.000    9.835286 10.51785
------------------------------------------------------------------------------我们可以发现政策变量的系数虽然显著但存在较大偏误，并且置信区间不包含真实政策效果 10 ，说明未纳入时间趋势项的 DID 模型不能有效识别政策效应。
3.2.2 加入时间趋势项

将时间趋势项纳入模型，对 (8) 式进行实现：
///实现(8)式模型
clear
use "DID_Time_Trend.dta"
reg y i.State##c.T i.time c.D#c.post x1 x2, rStata 估计结果如下：
note: 2009.time omitted because of collinearity

Linear regression                            Number of obs    =       600
                                             F(14, 585)       = 67886.42
                                             Prob > F       =    0.0000
                                             R-squared       =    0.9994
                                             Root MSE       =    1.0208

------------------------------------------------------------------------------
         |             Robust
         y |    Coef. Std. Err.    t P>|t|    [95% Conf. Interval]
-------------+----------------------------------------------------------------
   1.State | 4.832934 .2144808 22.53 0.000    4.411688 5.254181
         T | .4927767 .0265998 18.53 0.000    .440534 .5450193
         |
State#c.T |
      1  | .5696779 .0604302    9.43 0.000    .4509915 .6883644
         |
      time |
   2001  |  -.2609188 .1793334 -1.45 0.146 -.6131345    .091297
   2002  |  -.0852692 .1850952 -0.46 0.645 -.4488013    .278263
   2003  |  -.2698823 .1695362 -1.59 0.112    -.602856 .0630914
   2004  |  -.3877898 .1940886 -2.00 0.046 -.7689852 -.0065944
   2005  |  -.1348258 .180441 -0.75 0.455    -.489217 .2195653
   2006  |  -.2847543 .1578393 -1.80 0.072    -.594755 .0252464
   2007  | .0591873 .169159    0.35 0.727 -.2730455 .3914202
   2008  |  -.0942736 .1725591 -0.55 0.585 -.4331844 .2446373
   2009  |       0  (omitted)
         |
  c.D#c.post | 9.522704 .3503993 27.18 0.000    8.834511    10.2109
         |
      x1 | 4.993368 .0057933 861.91 0.000    4.981989 5.004746
      x2 | 3.007577 .008313 361.79 0.000    2.99125 3.023904
   _cons | 10.25255 .1806734 56.75 0.000    9.897704    10.6074
------------------------------------------------------------------------------从回归结果看，我们最为关心的政策变量系数现在仍是高度显著的，并且非常接近真实值 10，置信区间同样也包含 10，可见 (8) 式模型在这种情况下显著优于 (7) 式模型，所以此时我们有必要将时间趋势项纳入传统的 DID 模型中。
参考文献

Wooldridge J M. Introductory econometrics: A modern approach[M]. Nelson Education, 2016: pp.329-338.
李子奈, 潘文卿. 计量经济学[M]. 高等教育出版社, 2000: pp.156-163.
陈强. 高级计量经济学及 Stata 应用[M]. 高等教育出版社, 2014: pp.399-407.
ResearchGate Question: Is anyone familiar with Time Trends vs Time Dummies? -Link-
Economics Job Market Rumors
赵西亮. 基本有用的计量经济学[M]. 北京大学出版社, 2017: pp.147-162.
Angrist J D, Pischke J S. Mostly harmless econometrics: An empiricist's companion[M]. Princeton university press, 2008: pp.221-248.

连享会 - 效率分析专题
已上线：可随时购买学习+全套课件，课程主页 已经放置板书和 FAQs
主讲嘉宾：连玉君 | 鲁晓东 | 张宁
课程主页，微信版 https://gitee.com/arlionn/TE

相关课程

连享会-直播课 上线了！
http://lianxh.duanshu.com

免费公开课：

直击面板数据模型 - 连玉君，时长：1小时40分钟
Stata 33 讲 - 连玉君, 每讲 15 分钟.
部分直播课 课程资料下载 (PPT，dofiles等)

<hr/>课程一览

支持回看，所有课程可以随时购买观看。

Stata暑期班2020，连玉君，江艇，线上直播 9 天，2020.7.28-8.7 NEW！
效率分析-专题，连玉君，鲁晓东，张宁，视频-TFP-SFA-DEA，已上线，3天
文本分析/爬虫，游万海，司继春，视频-文本分析与爬虫，已上线，4天
空间计量系列，范巧，空间全局模型, 空间权重矩阵，空间动态面板，空间DID
研究设计，连玉君，我的特斯拉-实证研究设计，-幻灯片-
动态面板数据模型，连玉君，动态面板模型，-幻灯片-，课程主页
直击面板数据模型，连玉君，课程主页，[免费公开课，2小时]

Note: 部分课程的资料，PPT 等可以前往 连享会-直播课 主页查看，下载。

<hr/>

关于我们

Stata连享会 由中山大学连玉君老师团队创办，定期分享实证分析经验。直播间 有很多视频课程，可以随时观看。
连享会-主页 和 知乎专栏，300+ 推文，实证分析不再抓狂。
公众号推文分类： 计量专题 | 分类推文 | 资源工具。推文分成 内生性 | 空间计量 | 时序面板 | 结果输出 | 交乘调节 五类，主流方法介绍一目了然：DID, RDD, IV, GMM, FE, Probit 等。
公众号关键词搜索/回复 功能已经上线。大家可以在公众号左下角点击键盘图标，输入简要关键词，以便快速呈现历史推文，获取工具软件和数据下载。