金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
文章来源:微信公众号:EW Frontier
关注可了解更多的雷达、通信、人工智能相关代码。问题或建议,请公众号留言;
内容目录
摘要DOI主要原理主代码展示仿真结果
摘要
近年来提出的变分信号分解方法,如自适应线性调频模式分解(ACMD)和广义色散模式分解(GDMD)在各个领域引起了广泛的关注。然而,这些方法难以同时分离啁啾分量和色散分量。本文提出了一个变分广义非线性模式分解(VGNMD)框架来解决这个问题。VGNMD首先引入自适应时频融合与聚类(ATFFC)方法,提高噪声环境下信号时频分布(TFD)的抗噪性和分辨率,准确获取各模式的TFD。然后,模式类型的判别标准,建立了模式分为啁啾模式或色散模式的基础上,其时间-频率(TF)的脊。最后,以这些TF脊作为初始瞬时频率(IF)或初始群延迟(GD),应用变分优化算法精确重构模态并细化其IF或GD。仿真例子和实际应用蝙蝠回声定位信号分析和铁路轮轨故障诊断证明了VGNMD的有效性。结果表明,该方法可以同时准确地提取啁啾模和色散模,适用于分析具有不连续TF模式的非线性信号。
DOI
Detection of rub-impact fault for rotor-stator systems: A novel method based on adaptive chirp mode decomposition
https://doi.org/10.1016/j.jsv.2018.10.010
主要原理
对于旋转机械来说,旋转过程中转子和定子表面之间的摩擦冲击是一种常见且严重的故障。摩擦冲击故障将导致瞬时频率 (IF) 快速波动的调频 (FM) 振动信号 。由于当前时频(TF)方法的分辨率有限,很难提取快速波动的IF特征。最近提出的变分非线性啁啾模态分解(VNCMD)方法在分析强调频信号方面显示出明显的优势。然而,VNCMD解决了一个联合估计问题,该问题需要信号分量数量的先验信息,并可能导致不稳定问题。本文介绍了一种称为自适应啁啾模式分解(ACMD)的VNCMD的可处理版本,以提取摩擦冲击转子振动信号的快速波动IF。ACMD 采用贪婪算法来单独捕获每个信号分量。此外,利用ACMD估计的瞬时振幅和IF,我们得到了高分辨率的自适应TF谱,可以清楚地表示振动信号的摩擦冲击特征。首先通过动态仿真验证了基于ACMD的故障检测方法的有效性。然后,将该方法应用于某稠油催化裂化机组的振动信号,表明该方法在故障早期检测和多特征提取方面具有重要应用价值。
最近,文献[31]引入了一种强大的数据分析方法,称为变分非线性啁啾模态分解(VNCMD)。VNCMD是通过求解最优解调问题推导的,因此能够分析具有强FM特征的信号。最重要的是,VNCMD 直接在 TF 域中建模,它可以准确估计多分量 FM 信号的 IF 和瞬时幅度 (IA)。与 VMD 一样,VNCMD 通过联合优化技术同时估计所有信号分量。问题在于,必须事先知道信号底层分量的数量,并且联合估计方案在实际情况下可能不稳定,如参考文献[31]所述。该文介绍了一种可处理的VNCMD[32],称为自适应啁啾模态分解(ACMD),并提出了一种基于ACMD的摩擦冲击故障检测方法,用于估计振动信号的快速波动IF。ACMD采用类似于匹配追踪的贪婪算法[33\u201234],逐个递归估计信号分量。ACMD 更灵活,因为它需要更少的先验信息(例如,信号分量的数量)。此外,基于ACMD估计的IF和IA,我们得到了自适应TF频谱(ATFS),其分辨率比当前的TFD好得多。该故障检测方法的另一个重要优点是可以同时提取多个故障特征(如AM和FM),从而保证了更可靠的故障诊断。
其余文件的组织总结如下。在第 2 节中,在简要介绍了 VNCMD 之后,介绍了 ACMD。在第三节中,我们首先介绍了基于ACMD的摩擦断层特征提取方法,然后通过动态仿真验证了该方法的有效性。第4节介绍了所提出的故障检测方法的实际应用。最后,结论在第5节中得出。
主代码展示
- %%%%%%%%% instantaneous frequency initialization by detecting time-frequency ridge from STFT %%%%%%%%%%%%%%
- clc
- clear
- close all
- SampFreq = 500;
- t = 0:1/SampFreq:6;
- Sig1 = exp(-0.03*t).*cos(2*pi*(1.3+25*t + 4*t.^2 - 0.8*t.^3 + 0.07*t.^4));
- IF1 = 25 + 8*t - 2.4*t.^2 + 0.28*t.^3;
- Sig2 = 0.9*exp(-0.06*t).*cos(2*pi*(2.6+40*t + 8*t.^2 -1.6*t.^3 + 0.14*t.^4));
- IF2 = 40 + 16*t - 4.8*t.^2 + 0.56*t.^3;
- Sig3 = 0.8*exp(-0.09*t).*cos(2*pi*(3.9+60*t + 12*t.^2 -2.4*t.^3 + 0.21*t.^4));
- IF3 = 60 + 24*t - 7.2*t.^2 + 0.84*t.^3;
- Sig = Sig1 + Sig2 + Sig3;
- STD = 0.5;
- noise = addnoise(length(Sig),0,STD);
- Sign = Sig + noise;
- figure
- set(gcf,'Position',[20 100 320 250]);
- set(gcf,'Color','w');
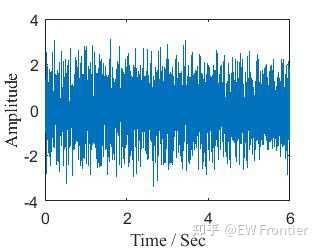
- plot(t,Sign,'linewidth',1);
- xlabel('Time / Sec','FontSize',12,'FontName','Times New Roman');
- ylabel('Amplitude','FontSize',12,'FontName','Times New Roman');
- set(gca,'FontSize',12)
- set(gca,'linewidth',1);
- axis([0 6 -4 4])
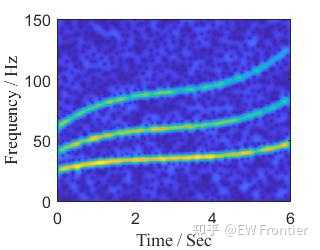
- %% STFT
- Ratio = 0;
- figure
- [tfSpec1,f] = STFT(Sign',SampFreq,1024,256);%128
- imagesc(t,f,abs(tfSpec1));
- axis([0 6 0 150]);
- set(gcf,'Position',[20 100 320 250]);
- xlabel('Time / Sec','FontSize',12,'FontName','Times New Roman');
- ylabel('Frequency / Hz','FontSize',12,'FontName','Times New Roman');
- set(gca,'YDir','normal')
- set(gca,'FontSize',12);
- set(gcf,'Color','w');
- %% parameter setting
- alpha0 = 1e-6; % or 1e-3 %or alpha = 2e-4; % if this parameter is larger, it will help the algorithm to find correct modes even the initial IFs are too rough. But it will introduce more noise and also may increase the interference between the signal modes
- beta = 1e-9; % 0.5e-4 this parameter can be smaller which will be helpful for the convergence, but it may cannot properly track fast varying IFs
- delta = 20; % control parameter for ridge detection
- tol = 1e-8;%
- %% Component 1 extraction
- index1 = findridges(tfSpec1,delta); % Time-frequency ridge detection
- iniIF1 = curvesmooth(f(index1),beta); % the initial guess for the IFs by ridge detection; the initial IFs should be smooth and thus we smooth the detected ridges
- [IFest1 IAest1 sest1] = ACMD(Sign,SampFreq,iniIF1,alpha0,beta,tol); % extract the signal component and its IA and IF
- %% Component 2 extraction
- residue1 = Sign - sest1; % obtain the residual signal by removing the extracted component from the raw signal
- [tfSpec2,f] = STFT(residue1',SampFreq,1024,256); % STFT of the residual signal
- index2 = findridges(tfSpec2,delta); % IF initialization by finding ridge curve of the STFT of the residue signal
- iniIF2 = curvesmooth(f(index2),beta); % smooth the ridge curve
- [IFest2 IAest2 sest2] = ACMD(residue1,SampFreq,iniIF2,alpha0,beta,tol); % extract the component 2 and its IA and IF from the residue signal
- %% Component 3 extraction
- residue2 = residue1 - sest2; % obtain the residual signal by removing the extracted component
- [tfSpec3,f] = STFT(residue2',SampFreq,1024,256); % STFT of the residual signal
- index3 = findridges(tfSpec3,delta); % IF initialization by finding ridge curve of the STFT of the residue signal
- iniIF3 = curvesmooth(f(index3),beta); % smooth the ridge curve
- [IFest3 IAest3 sest3] = ACMD(residue2,SampFreq,iniIF3,alpha0,beta,tol); % extract the component 2 and its IA and IF from the residue signal
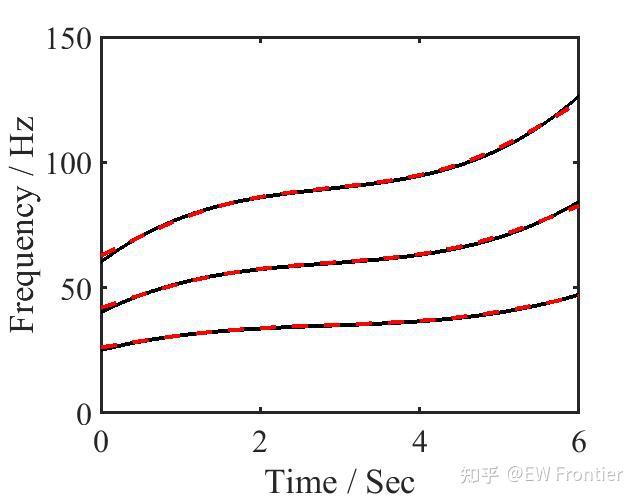
- %% initial IF
- figure
- plot(t,[IF1;IF2;IF3],'k','linewidth',3) % true IFs
- hold on
- plot(t,[iniIF1;iniIF2;iniIF3],'r--','linewidth',3) % initial IFs
- set(gcf,'Position',[20 100 640 500]);
- xlabel('Time / Sec','FontSize',24,'FontName','Times New Roman');
- ylabel('Frequency / Hz','FontSize',24,'FontName','Times New Roman');
- set(gca,'YDir','normal')
- set(gca,'FontSize',24);
- set(gca,'linewidth',2);
- set(gca,'FontName','Times New Roman')
- set(gcf,'Color','w');
- axis([0 6 0 150]);
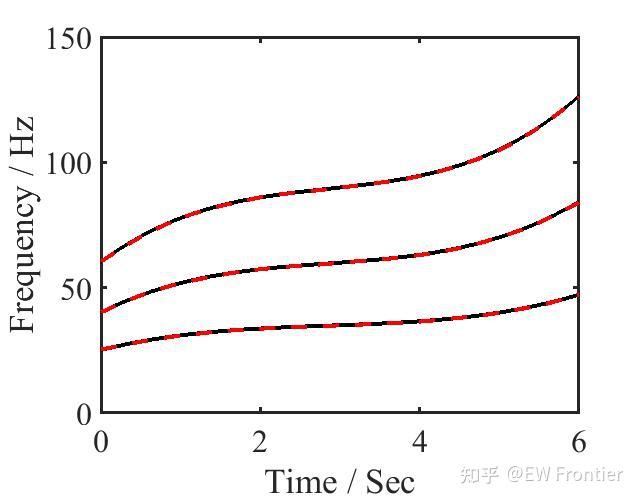
- %% estimated IF
- figure
- plot(t,[IF1;IF2;IF3],'k','linewidth',3) % true IFs
- hold on
- plot(t,[IFest1;IFest2;IFest3],'r--','linewidth',3) % finally estimated IFs
- set(gcf,'Position',[20 100 640 500]);
- xlabel('Time / Sec','FontSize',24,'FontName','Times New Roman');
- ylabel('Frequency / Hz','FontSize',24,'FontName','Times New Roman');
- set(gca,'YDir','normal')
- set(gca,'FontSize',24);
- set(gca,'linewidth',2);
- set(gca,'FontName','Times New Roman')
- set(gcf,'Color','w');
- axis([0 6 0 150]);
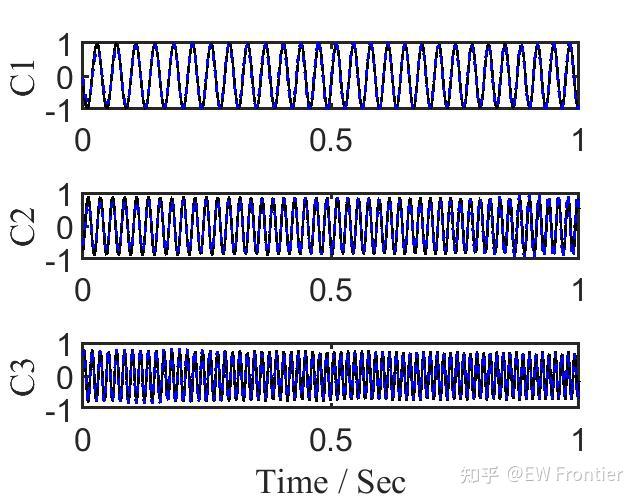
- %% Reconstructed modes
- figure
- set(gcf,'Position',[20 100 640 500]);
- subplot(3,1,1)
- set(gcf,'Color','w');
- plot(t,Sig1,'k','linewidth',2) % true signal mode
- hold on
- plot(t,sest1,'b--','linewidth',2) % estimated mode
- ylabel('C1','FontSize',24,'FontName','Times New Roman');set(gca,'YDir','normal')
- set(gca,'FontSize',24);
- set(gca,'linewidth',2);
- axis([0 1 -1 1])
- subplot(3,1,2)
- set(gcf,'Color','w');
- plot(t,Sig2,'k','linewidth',2)
- hold on
- plot(t,sest2,'b--','linewidth',2) % estimated mode
- ylabel('C2','FontSize',24,'FontName','Times New Roman');
- set(gca,'YDir','normal')
- set(gca,'FontSize',24);
- set(gca,'linewidth',2);
- axis([0 1 -1 1])
- subplot(3,1,3)
- set(gcf,'Color','w');
- plot(t,Sig3,'k','linewidth',2)
- hold on
- plot(t,sest3,'b--','linewidth',2) % estimated mode
- ylabel('C3','FontSize',24,'FontName','Times New Roman');
- xlabel('Time / Sec','FontSize',24,'FontName','Times New Roman')
- set(gca,'YDir','normal')
- set(gca,'FontSize',24);
- set(gca,'linewidth',2);
- axis([0 1 -1 1])
- %% adaptive time-frequency spectrum
- band = [0 SampFreq/2];
- IFmulti = [IFest1;IFest2;IFest3];
- IAmulti = [IAest1;IAest2;IAest3];
- [ASpec fbin] = TFspec(IFmulti,IAmulti,band);
- figure
- imagesc(t,fbin,abs(ASpec));
- axis([0 6 0 150]);
- set(gcf,'Position',[20 100 640 500]);
- xlabel('Time / Sec','FontSize',24,'FontName','Times New Roman');
- ylabel('Frequency / Hz','FontSize',24,'FontName','Times New Roman');
- set(gca,'YDir','normal')
- set(gca,'FontSize',24);
- set(gcf,'Color','w');
- colorbar('YTickLabel',{' '})
- %% SNR of the reconstructed signal mode
- SNR1 = SNR(Sig1,sest1) %
- SNR2 = SNR(Sig2,sest2)
- SNR3 = SNR(Sig3,sest3)
- %% Relative errors of the initial IFs
- iniRE1 = norm(iniIF1-IF1)/norm(IF1)
- iniRE2 = norm(iniIF2-IF2)/norm(IF2)
- iniRE3 = norm(iniIF3-IF3)/norm(IF3)
- %% Relative errors of the finally estimated IFs
- RE1 = norm(IFest1-IF1)/norm(IF1) % one can find that the accuracy of the finally estimated IFs is significantly improved compared with the initial IFs (by ridge detection) whose accuracy is limited by the resolution of the TFR.
- RE2 = norm(IFest2-IF2)/norm(IF2)
- RE3 = norm(IFest3-IF3)/norm(IF3)
- %%%%% In practice, the above procedure can be executed iteratively until the energy of the residual signal is smaller than a threshold

 |
|
 /3
/3 