衡量时间序列相似度的方法-从欧氏距离到DTW及其变种

临床医师

0、摘要

根据时间序列本身的不同特点，时间序列相似度的衡量（时间序列间距离的度量）存在多种方法。本文从欧氏距离出发，进一步延伸至Dynamic Time Warping（DTW）、一些DTW存在的缺点和相关的解决办法以及DTW的两个变种Derivative Dynamic Time Warping（DDTW）和Weighted Dynamic Time Warping（WDTW）。
1、前言/背景

在众多广泛的科研领域中，时间序列是一种无处不在的数据格式。对于时间序列相关的研究而言，其中一种最常见的需求就是比较两个时间序列是否相似。有效地比较时间序列间的相似度在很多科学/工程任务中非常必要且关键，如：分类/聚类/语音识别/步态识别等。
以某个生产制造环节中针对产成品某项（些）特征所收集到的时间序列数据为例。首先，所收集到的代表良品和次品的时序数据中在某些特定特征上有区别，且这些区别具有与领域知识相关的特定物理含义；其次，由于生产制造过程中的本身特性，所收集到的时序数据长度是不相等的；再而言，次品的产生存在多种原因，换句话说，产成品不只可以进行二分类成良品和次品两个种类，而是可以进一步区分为良品、次品种类1、次品种类2、次品种类3等多种类；最后，跟很多实际生产制造中的数据一样，良品数据量远大于次品数据量，次品继续细分的各种类次品数据更是少之甚少，整体存在严重的数据不平衡问题。
为了在正常生产制造过程中实现良品和不同种次品的多分类任务，比较所收集到的时间序列间的相似度是重要的一步。从直觉上不难理解，比较时间序列的相似度等同于计算时间序列间的“距离”，两个时间序列之间的“距离”越大，二者的相似度则越小，反之同理。
故本文基于此从欧氏距离出发，进一步延伸至Dynamic Time Warping（DTW）、一些DTW的缺点和相关的解决办法以及DTW的两个变种Derivative Dynamic Time Warping（DDTW）和Weighted Dynamic Time Warping（WDTW）。鉴于关于DTW的细节已经有很多优质博文介绍，故本文只阐述基本概念、更多关注不同方法间的区别、过渡的逻辑以及不同方法所适用的问题。
2、欧氏距离

提到衡量时间序列之间的距离，欧氏距离（Euclidean Distance）是最直接的方法，它概念简单，在此不赘述。当应用欧氏距离来比较两个时间序列时，序列与序列之间的每一个点按顺序建立起了一对一的对应关系，根据点与点之间的对应关系计算其欧氏距离作为两个时间序列之间的距离度量（相似度）。如下图1所示：



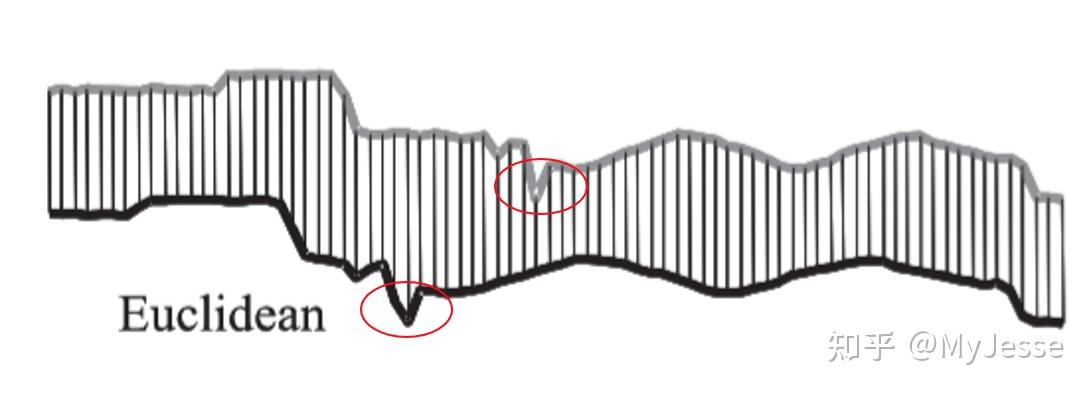
图1. 两个等长时间序列间的欧氏距离

在应用欧氏距离时，第一个时间序列中的第 i 个点分别与第二个时间序列中的第 i 个点形成一一对应。然而，欧氏距离在某些情况下会出现问题，如下图2所示：



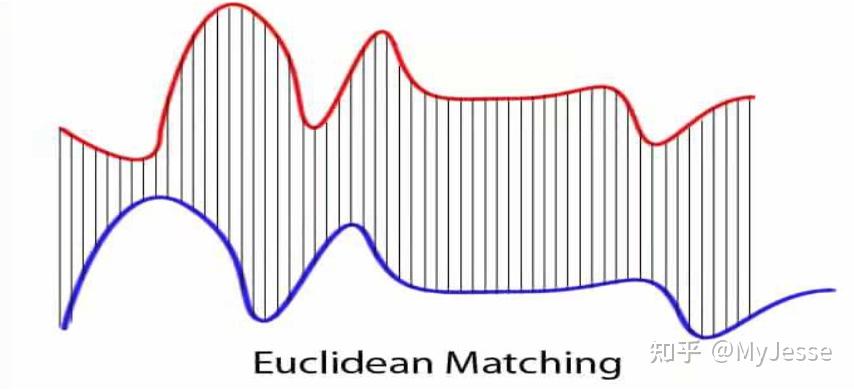
图2. 两个不等长时间序列间的欧氏距离是否可行？

当两个时间序列的长度不相等时，较长的一个时间序列总会剩下无法被匹配到的点，这种情况如何计算欧氏距离？毫无疑问，此时欧氏距离不再可行。此外，如图1中红圈所示，两个时间序列在时间轴上有一定的平移但总体的趋势是相似的，自然地，当我们想人为对齐图1中两个时间序列时，红圈中的两个向下凸起的点应该相互对应起来。很显然，欧氏距离的这种方式按顺序点对点的方法无法满足我们的需求。
综上，在时间序列间的距离度量上，欧氏距离有以下限制：（1）只适用于处理等长的时间序列；（2）在将时间序列对齐时无法考虑 X 轴上的变化，导致有时对齐出现不自然。
特别地，作为一种常见的标准距离度量，欧氏距离是另一种更为广泛的距离度量——闵式距离（Minkowski distance）当p取值为2时的特例。闵式距离中p=1时和p=infinity时，分别对应曼哈顿距离和两个时间序列点与点之间距离差值的最大值。
3、DTW (Dynamic Time Warping)

针对上文提到的欧氏距离无法处理不等长数据、处理等长数据时对齐不自然的两个主要问题，为了解决不等长数据的距离度量和匹配问题，上世纪70年代，日本学者Itakura等人提出了DTW。在过去的几十年里，DTW已经被广泛应用于孤立词语音识别、手势识别、数据挖掘和信息检索等场景中，DTW一度是语音识别的主流方法。DTW的原理此处简述如下：
对于两个不等长的时间序列Q和C，长度分别为n和m：


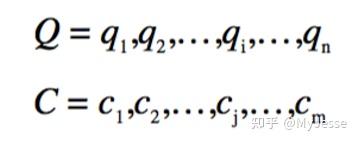
要使用DTW来对齐两个不等长的时间序列，需要构建一个n*m的距离矩阵，矩阵中的第i行第j列所对应的元素代表的就是序列中点 q_{i} 和点 c_{j} 的距离 D\left( q_{i}，c_{j} \right) ，通常情况下这里会使用欧氏距离，所以 D\left( q_{i}，c_{j} \right) = \left( q_{i}-c_{j} \right)^{2} 。可参见下图3：



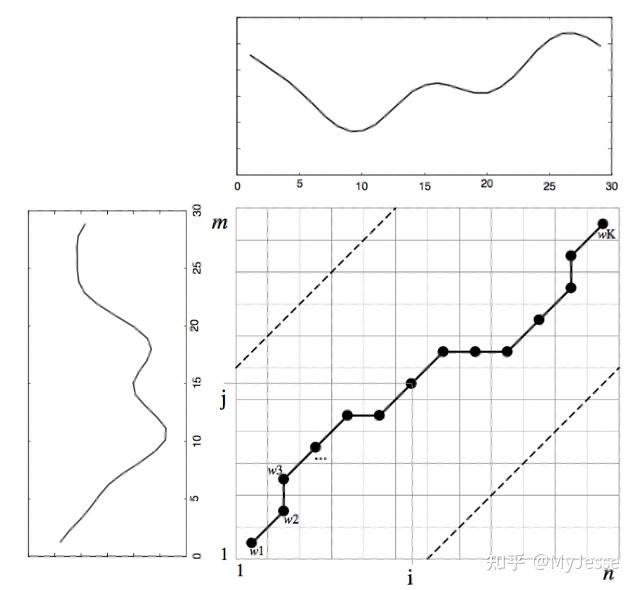
图3. DTW中的warping path示意图

上图所示为n*m的矩阵，每一个方格代表矩阵中的每一个元素。对于两个时间序列而言，DTW抛开了欧氏距离的限制，其本意是要寻找到一个连续的包含两个时间序列中所有点互相对应的一个匹配关系（这种匹配可以是第 i 个点对应第 j  个点， i\ne j ）,这些匹配关系的集合共同构成了图3中的黑色实线warping path W：


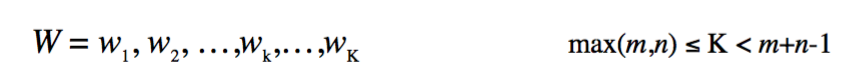
要进行DTW匹配，warping path W需满足以下条件：
1-边界性（Boundary conditions）： W_{1} = \left( 1,1 \right) 和 W_{k} = \left( n,m \right) ，简而言之，两个经DTW对齐的时间序列应该首对首、尾对尾相连，反映到距离矩阵中就是warping path应从一个角落出发、在对角线方向上的另一个角落停止。
2-连续性（Continuity）：每次warping path向下一步移动必须是连续的，反映到距离矩阵中就是下一步只能在原方格的相邻方格中选取（方向需满足对角线方向）。数学上可写成:对于W_{k} = \left( a,b \right) ， W_{k-1} = \left( a^{'}, b^{'} \right) ，需满足 a-a^{'}\leq 1 ， b-b^{'}\leq 1 。
3-单调性（Monotonicity）：两个时间序列间的对应必须按照顺序进行，warping path不能有交叉。数学上可写成： W_{k} = \left( a,b \right) ， W_{k-1} = \left( a^{'}, b^{'} \right) ，需满足 a-a^{'}\geq0 ， b-b^{'}\geq0 。
满足这些条件的W还是有很多个，DTW只寻找能够最小化warping cost的W：


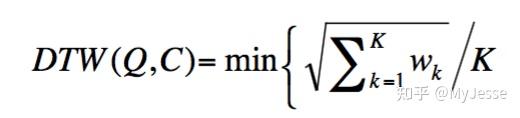
在上式中，K是warping path的长度，除以K可以消除不同长度的warping path的影响。
最终，两个不等长时序数据的对应关系可以通过动态规划来求解以下递归式得到：


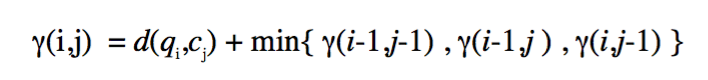
其中， \gamma\left( i，j \right) 是到距离矩阵第 i 行第 j 列时所积累的warping path的总距离。
4、 DTW面临的问题及其解决方案

尽管DTW已经被成功应用到很多领域中，DTW依然存在缺点：有时DTW会在对齐时产生不自然的扭曲/翘曲。如下图4所示：



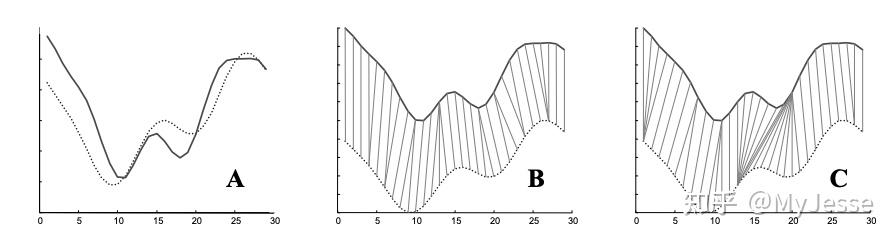
图4. 合成数据中DTW在对齐时产生的Singularities

A中实线、虚线所展示的是两条合成信号（均值、方差都相同），B中展示的是自然的“feature to feature”的对应，而C中展示的则是DTW的结果。不难发现，DTW没能自然地将图形中的波峰与波峰相对应，反而产生了一个序列中的一个点对应另外一个序列中的多个点的情况，这种情况被称为“Singularities”。出现这种情况的原因是DTW算法试图通过扭曲X轴来解释Y轴上的变化。
为了解决“Singularities”问题，过去的研究提出了很多方案，大致可归为以下三类：
1-Windowing：归根结底，出现singularities就是因为两个时间序列上相隔很远的点仅因为值相同/相近容易被warping到一起。可以限制DTW在warping过程中的能选择的范围来解决singularities，具体可以通过设置一个warping window来实现，故称之为Windowing方法。
数学上可写作：\left| i-\left( n/\left( m/j \right) \right)\right|<R ， R 作为window width是一个正整数。图3中两虚线所夹范围即为经window限制后的范围，此时warping path就只能在此区域内。
2-Slope weighting: 当传统DTW中的递归式改为下式时，即可实现slope weighting。


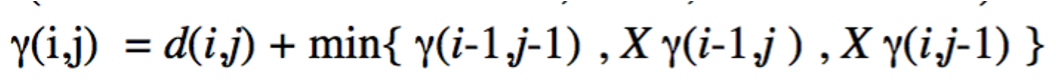
不难发现，唯一的区别在于在min函数中的后两项前加了 X ， X 为一个正实数。当对 X 的值进行调整时，可以使得warping path的方向（slope）会有一定的调整。 X 取较大值时，warping path的选择会更多的朝向对角线方向。
3-Step patterns: 改变传统DTW中的递归式为下式可以实现改变warping path step。


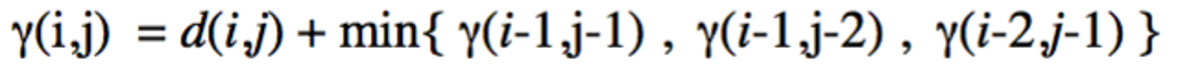
将传统DTW中的递归式和上式分别可视化如下图5中A、B所示：



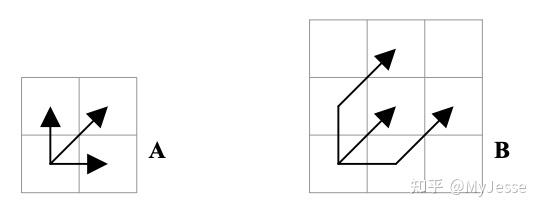
图5. 两种不同step pattern的递归式的可视化

A所对应的即为传统DTW的递归式，下一步只能在距离矩阵中相邻的三个方格中选取，而B中所对应的就是改变了step后的递归式。相较于A中，B中对于每一个第一步没有沿着对角线方向走的方格都再朝其所在方格的对角线方向移动一步，这样即可实现改变step pattern。
总的来说，以上三类解决方案在一定程度上对解决singularities有一定帮助，然而，它们仍然存在以下缺点：
（1）有可能错过正确的warping path。以上三类方法都是在没有任何前提条件的情况下人为地对warping path进行限制和调整来减少翘曲，这很有可能会错过真正正确的warping path。
（2）参数的选择没有明确的指导。在Windowing方法中 R 值的选取、Slope weighting方法中 X 都是人为视具体场景主观调整、没有明确标准的。
5、Derivative Dynamic Time Warping (DDTW)

实际上，DTW之所以造成“Singularities”，本质上是由于DTW算法本身所考虑的特征决定的：DTW算法只考虑数据点在Y轴上的值。
例如：两个数据点 q_{i} 和 c_{j} 的值相同，但是 q_{i}  位于一个时间序列的上升趋势部分，而 c_{j} 位于一个时间序列的下降趋势部分。对于DTW而言，很容易将这两个点匹配在一起，因为它们的值相同。然而，从直觉上来说，我们很难把两个趋势相反的部分匹配在一起。为了避免DTW只考虑Y轴的值造成“Singularities”问题，DDTW出现了。
DDTW不考虑数据点的Y轴的值，而是考虑更高层次的特征——时序数据的“形状”。该方法通过计算时序数据的一阶导数来获取与“形状”相关的信息，所以被称为Derivative DTW。
DDTW本身的概念也很简单，对于传统DTW而言，距离矩阵中的元素即为两个点 q_{i} 和 c_{j} 之间的距离；然而对于DDTW而言，此时的“距离矩阵”中的元素不再是两点之间的距离，而是时序数据在两点处一阶导数的差值的平方。尽管有多种方法估计一阶导数，出于简便和拓展性，DDTW中的一阶导数估计采用以下方法：


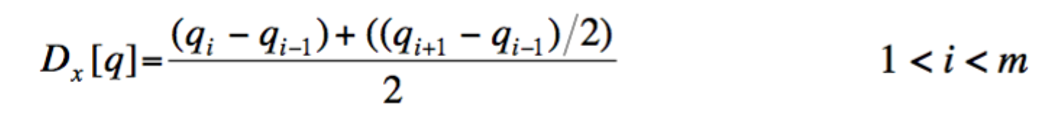
不难发现，在 q_{i} 点处一阶导数的估计就是通过该点和该点左边点的直线斜率与通过该点左边点和该点右边点的直线斜率的平均数。Keogh, E. J., & Pazzani, M. J.提到，在只考虑两个数据点的情况下，这种估计方法面对outliers更为稳定。
需要注意的是，这种一阶导数的估计方法无法计算时序数据的第一个数据点和最后一个数据点的一阶导数，在实际操作时可以用第二个数据点和倒数第二个数据点的导数来替代。此外，对于高噪声的数据集可以在估计一阶导数之前先做exponential smoothing。
6、Weighted Dynamic Time Warping (WDTW)

上文提到，经典的DTW算法在匹配两个时间序列上的点时仅考虑Y轴上的值，而不考虑所匹配的点在X轴上的差别，因此会造成时序数据匹配时的“Singularities”问题。
归根结底，“Singularities”问题在某种程度上就源于只考虑Y轴的值，第一个序列上的一个点可以跟第二个序列上的另一个很远（此处“远”指的是X轴的距离/序数）的点匹配起来，加上DTW中warping path的连续性、单调性条件，造成了时序数据对齐过程中的各种翘曲/扭曲。
DDTW通过考虑“形状”利用估计时序数据的一阶导数来解决这个问题，而WDTW则采用了不同的思路。简单来说，WDTW选择在计算两个序列上的两个点之间欧氏距离时加上一个weight，而这个weight与两个点之间的X轴上的距离有关系。具体如下（p=2）：


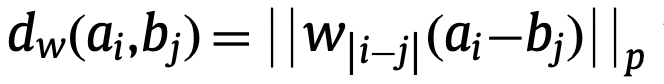
如上式，p=2时为计算两个序列上的两个点 a_{i} 和 b_{j} 的欧氏距离。此处的 w_{\left| i-j \right|} 即为与两个点在X轴上的距离（phase difference）相关的weight。WDTW通过计算两点欧氏距离时添加一个weight的方法，为解决“Singularities”问题提供了新的思路：weighted DTW本质上是一种penalized-based DTW，当 \left| i-j\right| 的值较大（两个点在X轴上距离较大）时，通过赋予一个较大的 w_{\left| i-j \right|} 值，则可避免算法将两个距离较大的点匹配在一起。
针对WDTW，Jeong, Y. S., Jeong, M. K., & Omitaomu, O. A.等人还提出了一个logistic weight function来赋予权重，感兴趣的读者可自行查阅原文。值得一提的是，当 w_{\left| i-j \right|} 是一个常数的时候，此时的WDTW不会对于X轴上距离不同的点的惩罚是相同的，所以等同于传统的DTW；当 w_{\left| i-j \right|} 的值极大时，此时的WDTW对于X轴上距离不同的点惩罚也极大，甚至第i个点和第i-1个点的匹配也不行，此时的WDTW即对应传统的欧氏距离。
7、总结与补充

综上，本文从只能处理等长数据且容易造成不自然对齐的欧氏距离出发，我们逐步论述了DTW出现的原因和重要性。进一步，我们发现传统DTW算法带来的singularities问题可以在windowing、slope weighting、step pattern等方法下得到一定改善。然而，从算法考虑的特征层面出发，为了解决DTW算法匹配时序数据时可能存在的singularities问题，DDTW提出考虑更高层次的特征——形状，并利用估计一阶导数来实现。最后，WDTW显示出它是一个更大的可以包含欧氏距离、传统DTW的距离度量框架，同时WDTW也通过考虑了时序数据匹配过程中的phase difference为解决singularities问题提供了另一种思路。
源于距离矩阵的构建，DTW及其变种的算法复杂度是相同的，均为 O\left( mn \right) 。此外，本文所述内容并未涉及DTW在大规模数据集检索中的算法加速问题。实际上，在大规模的应用中，过去的研究已经有了很多方法来对DTW算法进行加速，如：FastDTW，LB_Keogh等。
8、主要参考文献

Keogh, E., & Ratanamahatana, C. A. (2005). Exact indexing of dynamic time warping.Knowledge and information systems,7(3), 358-386.
Keogh, E. J., & Pazzani, M. J. (2001, April). Derivative dynamic time warping. InProceedings of the 2001 SIAM international conference on data mining(pp. 1-11). Society for Industrial and Applied Mathematics.
Jeong, Y. S., Jeong, M. K., & Omitaomu, O. A. (2011). Weighted dynamic time warping for time series classification.Pattern recognition,44(9), 2231-2240.
维基百科.

原文地址：https://zhuanlan.zhihu.com/p/389388258