基于前馈神经网络的时间序列异常检测算法

John

基于前馈神经网络的时间序列异常检测算法

引言

在时间序列异常检测中，特征工程往往是非常繁琐而复杂的，怎样才能够减少时间序列的特征工程工作量一直是一个关键问题。在本文中，作者们提出了一个新的思路，使用深度学习的办法来进行端到端的训练，从而减少时间序列的特征工程。
提到深度学习，大家都能够想到卷积神经网络（Convolutional Neural Network ）在图像识别中的优异表现，能够想到循环神经网络（Recurrent Neural Network）在机器翻译和文本挖掘领域中所取得的成绩。而一旦提到时间序列，一般的人都能够想到使用 ARIMA 模型或者 LSTM 模型来拟合周期型的时间序列，或者使用其他算法来进行时间序列的异常检测。在这篇文章中，既不谈 CNN 和 LSTM 等深度学习模型，也不谈如何使用 LSTM 来拟合时间序列，本文将会介绍如何使用无特征层的前馈神经网络 Feedforward Neural Network（端到端）来进行时间序列的异常检测。并且将会介绍如何使用前馈神经网络，来拟合各种各样的时间序列特征。本篇论文《Feedforward Neural Network for Time Series Anomaly Detection》目前已经挂在 Arxiv 上，有兴趣的读者可以自行参阅：https://arxiv.org/abs/1812.08389。
时间序列异常检测

时间序列异常检测的目的就是在时间序列中寻找不符合常见规律的异常点，无论是在学术界还是工业界这都是一个非常重要的问题。而时间序列异常检测的算法也是层出不穷，无论是统计学中的控制图理论，还是指数移动平均算法，甚至近些年最火的深度学习，都可以应用在时间序列的异常检测上面。在通常情况下，时间序列的异常点是十分稀少的，正常点是非常多的，因此，通常的套路都是使用统计判别算法和无监督算法作为第一层，把有监督算法作为第二层，形成一个无监督与有监督相结合的框架。使用无监督算法可以过滤掉大量的正常样本，将我们标注的注意力放在少数的候选集上；使用有监督算法可以大量的提升准确率，可以把时间序列异常点精确地挑选出来。这个框架之前也说过多次，因此在这里就不再做赘述。



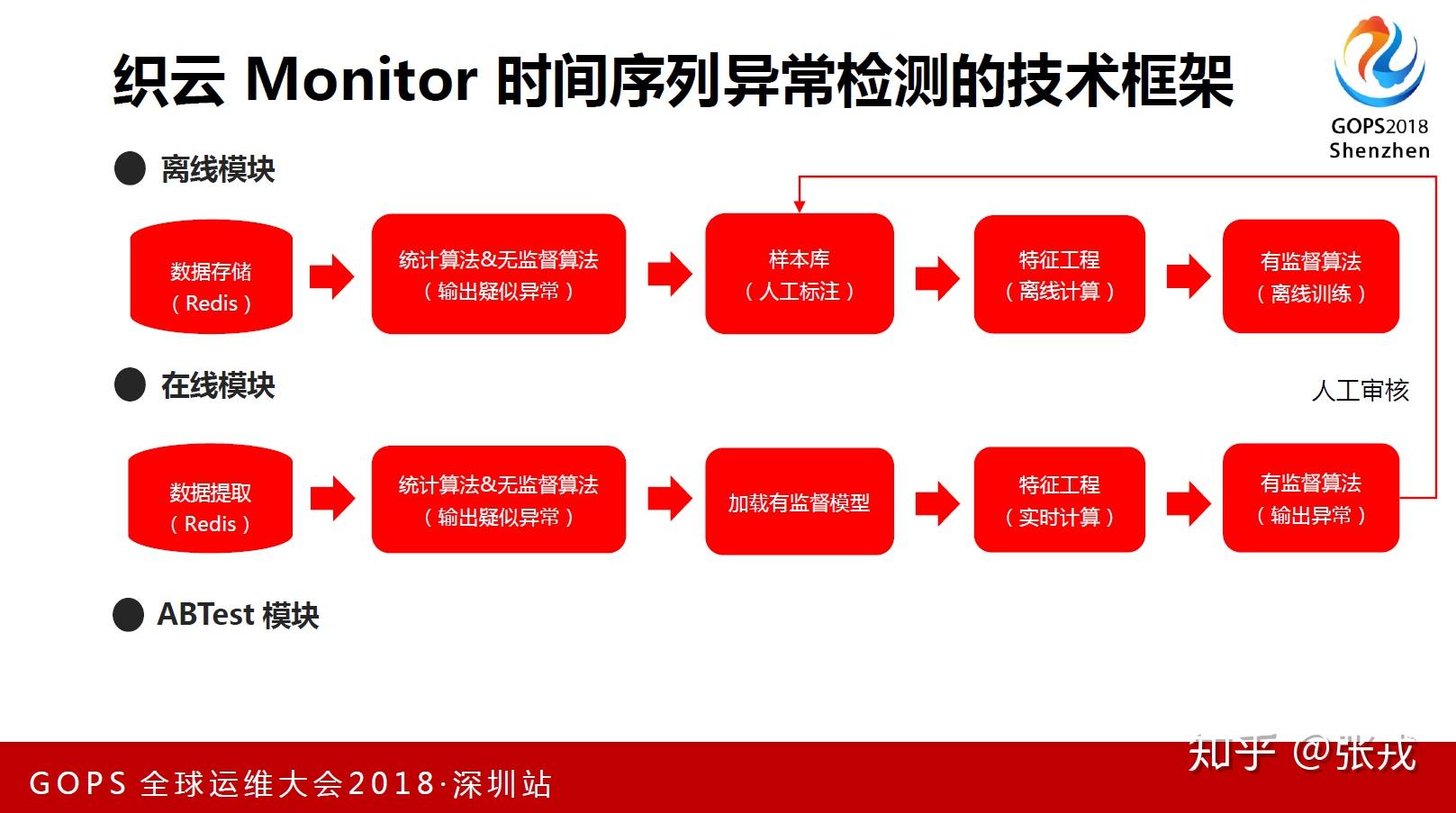
提到第二层的有监督学习算法，通常来说就包括逻辑回归，随机森林，GBDT，XGBoost，LightGBM 等算法。在使用这些算法的时候，不可避免地就需要构造时间序列的特征，也就是人工撰写特征工程的工作。提到时间序列的特征，一般都会想到各种各样的统计特征，例如最大值，最小值，均值等等。除了统计特征之外，我们还可以使用一些简单的时间序列模型，例如移动平均算法，指数移动平均算法等去拟合现有的时间序列，所得到的拟合值与实际值的差值就可以作为时间序列的拟合特征。除了统计特征和拟合特征之外，我们还可以根据时间序列的走势，例如周期型，毛刺型，定时任务型来构造出时间序列的分类特征，用于时间序列形状的多分类问题。因此，就笔者的个人观点，时间序列的特征大体上可以分成统计特征，拟合特征，周期性特征，分类特征等几大类。



在机器学习领域下，可以使用准确率和召回率来评价一个系统或者一个模型的好坏。在这里，我们可以使用 negative 标签来表示时间序列的异常，使用 positive 标签来表示时间序列的正常。因此模型的召回率，准确率，F1-Score 可以如下表示：
\text{Recall}=\frac{\text{the number of true anomalous points detected}}{\text{the number of true anomalous points}}=\frac{TN}{TN+FP},
\text{Precision}=\frac{\text{the number of true anomalous points detected}}{\text{the number of anomalous points detected}}=\frac{TN}{TN+FN},
\text{F1-Score} = \frac{2 \cdot \text{precision} \cdot \text{recall}}{\text{precision}+\text{recall}}.



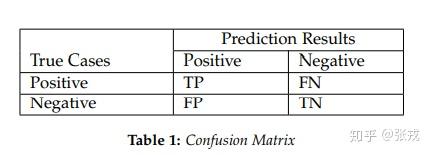
而时间序列异常检测工作也不是一件容易的事情，通常来说它具有以下几个难点：

• 海量时间序列。通常情况下，时间序列不仅仅是按照天来收集数据的，有可能是按照小时，甚至分钟量级来收集数据。因此，在一些情况下，时间序列的数量和长度都是非常大的。
  
• 类别不均衡。一般来说，在时间序列异常检测领域，正常样本是非常多的，异常样本是非常少的。在这种情况下，训练模型的时候通常都会遇到类别不均衡的问题。
  
• 样本不完整。通常来说，时间序列异常检测领域，是需要用人工来标注样本的，这与推荐系统是非常不一样的。这种情况下，很难通过人工标注的方式，来获得所有类型的样本数据。
  
• 特征工程复杂。时间序列有着自己的特点，通过特征工程的方式，确实可以获得不少的特征，但是随着时间序列种类的变多，特征工程将会越来越复杂。
  

基于以上几个难点，本篇论文提出了一种端到端（End to End）的训练方法，可以解决上面的一些问题。
深度学习的简单回顾

其实最简单的深度学习模型还不是 CNN 和 RNN，最简单的深度学习模型应该是前馈神经网络，也就是所谓的 FNN 模型。当隐藏层的层数较少的时候，当前的前馈神经网络可以称为浅层神经网络；当隐藏层的层数达到一定的数量的时候，当前的前馈神经网络就是所谓的深度前馈神经网络。下面就是一个最简单的前馈神经网络的例子，最左侧是输入层，中间有两个隐藏层，最右侧是输出层。



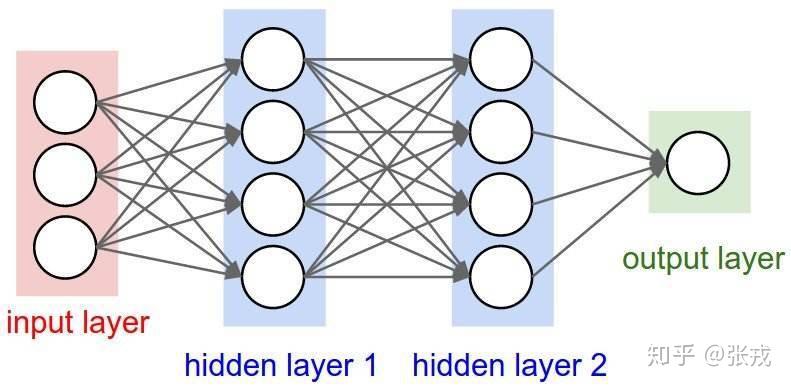
通常来说，前馈神经网络会涉及到必要的矩阵运算，激活函数的设置等。其中，激活函数的选择有很多，有兴趣的读者可以参见 tensorflow 的官网。比较常见的激活函数有 Sigmoid 函数，tanh 函数，relu 函数以及 relu 函数的各种变种形式（Leaky Relu, PreLu, Elu），以及 Softplus 函数等。
详细来说，以上的激活函数的具体函数表达式如下：
\sigma(x) = 1/(1+e^{-x}),
\tanh(x) = \sinh(x)/\cosh(x),
ReLU(x) = \max\{0,x\},
Leaky \text{ }ReLu(x) = \mathcal{I}_{\{x<0\}}\cdot(\alpha x) + \mathcal{I}_{\{x\geq 0\}}\cdot(x), \alpha\in \mathbb{R},
ELU(x) = \mathcal{I}_{\{x<0\}}\cdot(\alpha(e^{x}-1)) + \mathcal{I}_{\{x\geq 0\}}\cdot(x),
PreLU(x) = \mathcal{I}_{\{x_{j}<0\}}\cdot(a_{j}x_{j})+\mathcal{I}_{\{x_{j}\geq 0\}}(x_{j}),
selu(x) = \lambda\cdot(\mathcal{I}_{\{x<0\}}\cdot(\alpha e^{x}-\alpha) + \mathcal{I}_{\{x\geq 0\}}\cdot x), \lambda,\alpha\in\mathbb{R},
softplus(x) = \ln(1+e^{x}).
深度学习与时间序列的特征工程

通常来说，基于人工的时间序列特征工程会比较复杂，不仅需要包括均值方差等内容，还包括各种各样的特征，如统计特征，拟合特征，分类特征等。在这种情况下，随着时间的迁移，特征工程将会变得越来越复杂，并且在预测的时候，时间复杂度也会大量增加。那么有没有办法来解决这个问题呢？答案是肯定的。时间序列的一部分特征可以按照如下表格 Table 2 来表示：其中包括均值，方差等特征，也包括拟合特征和部分分类特征。



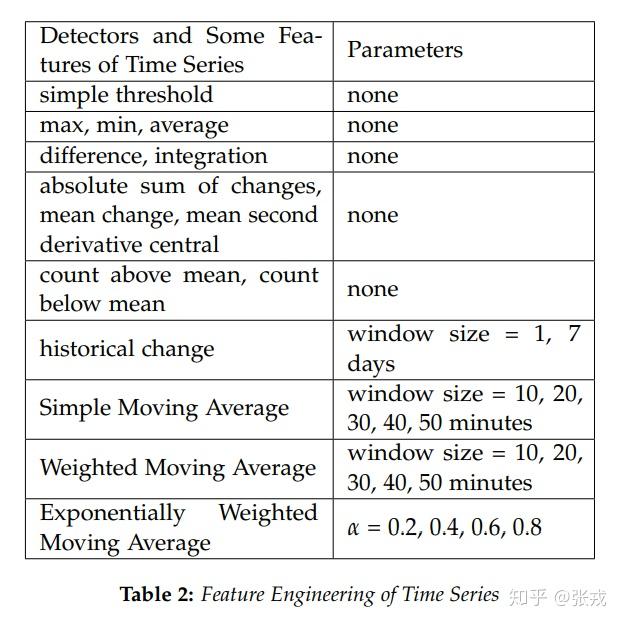
基于 Table 2，本篇论文的主要定理陈述如下：
Main Theorem. 对于任意正整数  n\geq 1 ，存在一个前馈神经网络 D  使得对于所有的时间序列 \boldsymbol{X}_{n}=[x_{1},\cdots,x_{n}] ，该神经网络的输入和输出分别是 \boldsymbol{X}_{n} 和表格 2 中 \boldsymbol{X}_{n} 的特征层。
下面，我们就来尝试使用深度学习模型来构造出时间序列的统计特征。首先，我们可以从几个简单的统计特征开始构造，那就是加法（add），减法（minus），最大值（max），最小值（min），均值（avg），绝对值（abs）。在构造时间序列  X_{n} = [x_{1},\cdots, x_{n}]  的以上统计特征之前，我们可以先使用神经网络构造出这几种运算方法。
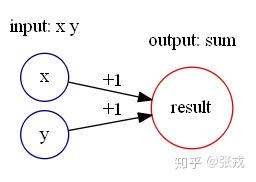
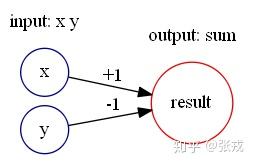
加法  add(x,y) = x+y  与减法 sub(x,y) = x-y 的构造十分简单，如下图构造即可：




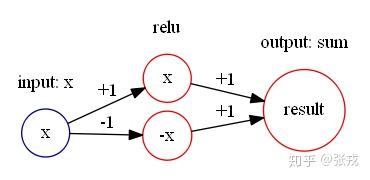
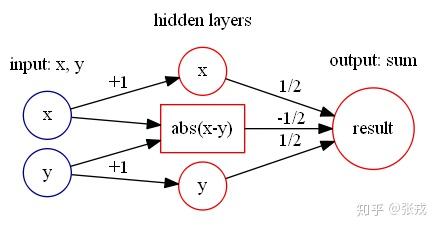
绝对值函数 abs(x) = |x|,  通过计算可以得到 abs(x) = relu(x) + relu(-x).  所以，可以构造如下的神经网络来表示绝对值函数：



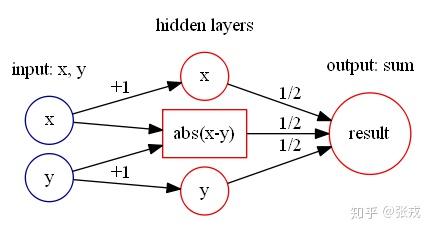
最大值函数   \max(x,y),   通过计算可以得到
\max(x,y) = (|x-y| + x+ y)/2.
所以，只要能够使用前面的神经网络来构造出绝对值模块，然后使用加减法就可以构造出最大值函数。



最小值函数  \min(x,y), 通过计算可以得到
\min(x,y) = (x+y-|x-y|)/2.
所以，同样使用前面的神经网络来构造出绝对值模块，然后使用加减法就可以构造出最小值函数。



在这种情况下，只要能够构造出两个元素的最大值，最小值函数，就可以轻易的构造出 n 个元素的最大最小值函数，因为
\max(x_{1},\cdots,x_{n}) = \max(x_{1},\max(x_{2},\max(x_{3},\cdots,\max(x_{n-1},x_{n}))),
\min(x_{1},\cdots,x_{n}) = \min(x_{1},\min(x_{2},\max(x_{3},\cdots,\min(x_{n-1},x_{n}))).
平均值函数  avg  指的是  avg(x_{1},\cdots, x_{n}) = (x_{1}+\cdots + x_{n})/n.



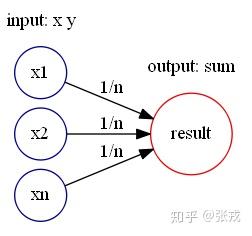
平方函数  y = x^{2}, 这个函数可以使用 Softplus 激活函数来表达。令 Softplus 为
f(x) = softplus(x) = \ln(1+e^{x}),
通过计算可以得到：
f(0) = \ln(2),
Df(x) = \sigma(x), Df(0) = 1/2,
D^{2}f(x) = \sigma&#39;(x) = \sigma(x)\cdot(1-\sigma(x)), D^{2}f(0) = 1/4,
D^{3}f(x) = \sigma&#39;&#39;(x), D^{3}f(0) = 0,
因此，Softplus 函数的 Taylor Series 是：
f(x) = softplus(x) = f(0) + Df(0)x+ \frac{1}{2!}D^{2}f(0)x^{2} + \frac{1}{3!}D^{3}f(0)x^{3}+o(x^{3})
= \ln(2) +\frac{1}{2}x+\frac{1}{8}x^{2}+o(x^{3}),
因此， x^{2} \approx 8\cdot(f(x) - \ln(2)-\frac{1}{2}x) = 8\cdot(\ln(1+e^{x})-\ln(2)-\frac{1}{2}x).  y=x^{2} 就可以用神经网络来近似表示：



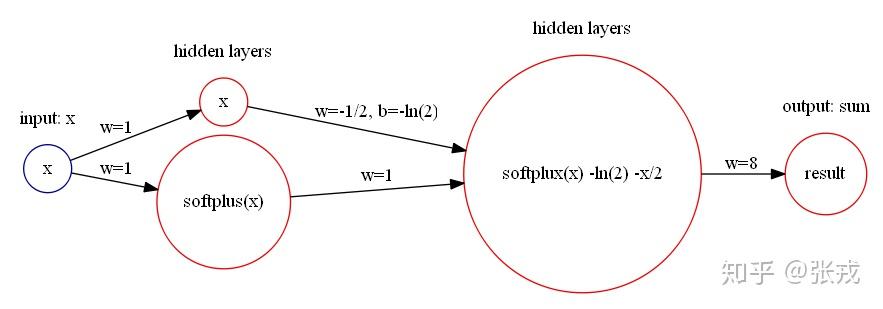
立方函数 y = x^{3}, 这个函数可以使用 Sigmoid 激活函数来表达。因为 Sigmoid 函数的 Taylor Series 是
\sigma(x) = \frac{1}{2}+\frac{1}{4}x-\frac{1}{48}x^{3}+o(x^{3}),
那么  x^{3} \approx -48\cdot(\sigma(x) - \frac{1}{2} -\frac{1}{4}x).  y=x^{3} 就可以用神经网络来近似表示：



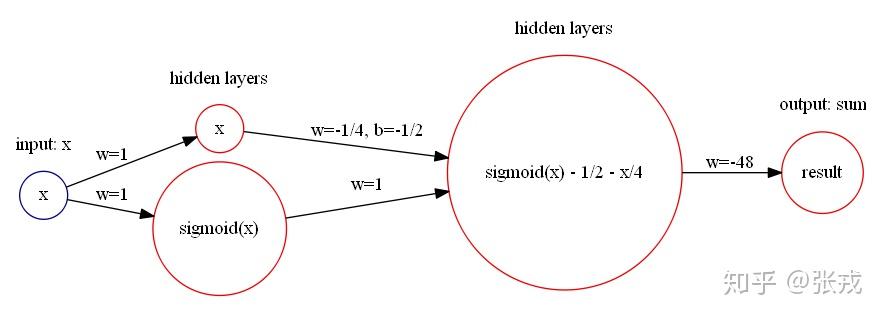
深度学习与时间序列的统计特征

提到时间序列的统计特征，一般指的都是已知的时间序列 X_{n} =[x_{1},\cdots,x_{n}] 的最大值，最小值等各种各样的统计指标。如果按照上文所描述的，以下特征都可以用神经网络轻松构造出来：
max: \max_{1\leq i\leq n}\{x_{1},\cdots,x_{n}\},
min: \min_{1\leq i\leq n}\{x_{1},\cdots,x_{n}\},
avg: \mu = \sum_{i=1}^{n}x_{i}/n,
variance: \sigma^{2}= \sum_{i=1}^{n}(x_{i}-\mu)^{2}/n, \text{ where } \mu = \sum_{i=1}^{n}x_{i}/n,
skewness: \sum_{i=1}^{n}[(x_{i}-\mu)/\sigma]^{3},
kurtosis: \sum_{i=1}^{n}[(x_{i}-\mu)/\sigma]^{4},
difference: x_{2}-x_{1}, x_{3}-x_{2},\cdots, x_{n}-x_{n-1},
integration: \sum_{i=1}^{n}x_{i},
absolute_sum_of_changes: E=\sum_{i=1}^{n-1}|x_{i+1}-x_{i}|,
mean_change: \frac{1}{n}\sum_{i=1}^{n-1}(x_{i+1}-x_{i}) = \frac{1}{n}(x_{n}-x_{1}),
mean_second_derivative_central: \frac{1}{2n}\sum_{i=1}^{n-2}(x_{i+2}-2x_{i+1}+x_{i}),
除了以上比较容易构造的特征之外，还有一类特征只为了计算个数的，例如 count_above_mean，count_below_mean 分别是为了计算大于均值的元素个数，小于均值的元素个数。那么最重要的就是要构造出计数函数 count。
回顾一下 NOT 逻辑计算门是：  1 \rightarrow 0, 0 \rightarrow 1.
这个逻辑门可以使用逻辑回归函数来估计，可以参见 \sigma 函数的图像，当 x>10 的时候， \sigma(x) \approx 1; 当 x<-10 的时候， \sigma(x)\approx 0. 因此，可以使用函数 f(x) =\sigma(-20x+10) 来估计 NOT 逻辑门。
当 x=1 时，  f(x) = f(1) = \sigma(-10) \approx 0;
当 x=0 时， f(x) = f(0) = \sigma(10)\approx 1.
下面，我们来考虑如何构造出一个函数来判断待测试值 x 是否大于常数 a.
令 f_{1}(x) = \sigma(-2\cdot 10^{4} \cdot relu(-x+a) + 10), 可以得到
当  x>a  时， f_{1}(x) = \sigma(10) \approx 1;
当  x<a-10^{-3}  时， f_{1}(x) = \sigma(-2\cdot 10^{4}\cdot (a-x) + 10)<\sigma(-10) \approx 0.
因此，所构造的函数  f_{1}(x) 近似于判断待测试值 x 是否大于常数 a.
下面，可以构造一个类似的函数来判断待测试值 x 是否小于常数  a.  令 f_{2}(x) = \sigma(-2\cdot 10^{4} \cdot relu(x-a) + 10), 可以得到
当  x<a  时， f_{2}(x) = \sigma(10)\approx 1;
当 x>a+10^{-3} 时， f_{2}(x) = \sigma(-2\cdot 10^{4}\cdot (x-a)+10) < \sigma(-10)\approx 0.
因此，所构造的函数 f_{2}(x) 近似于判断待测试值  x  是否小于常数  a.
回到时间序列的特征 count_above_mean 与 count_below_mean，可以先计算出均值 mean，然后计算时间序列  X_{n}=[x_{1},\cdots,x_{n}]  每个点与均值的差值，然后使用前面的神经网络模块计算出大于零的差值个数与小于零的差值个数即可。





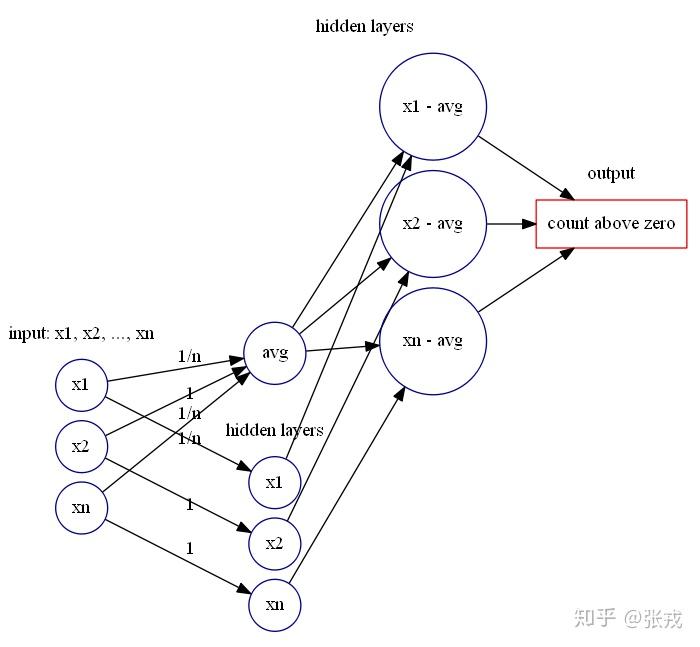
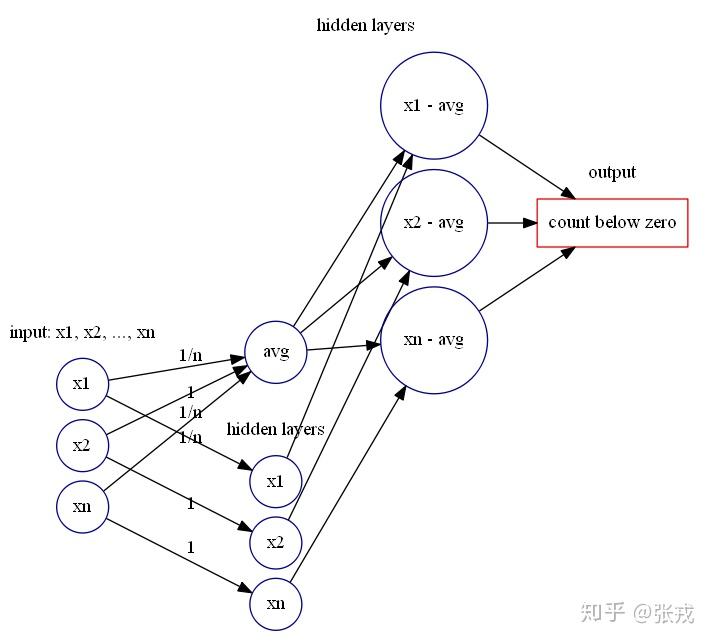
深度学习与时间序列的拟合特征

时间序列的拟合特征的基本想法是用一些简单的时间序列算法去拟合数据，然后使用拟合数据和真实数据来形成必要的特征。在这里，我们经常使用的算法包括移动平均算法，带权重的移动平均算法，指数移动平均算法等。下面，我们来看一下如何使用神经网络算法来构造出这几个算法。
移动平均算法
移动平均算法指的是，已知时间序列  X_{n} = [x_{1},\cdots,x_{n}],  我们可以使用一个窗口值 w\geq 1 得到一组光滑后的时间序列，具体来说就是：
SMA_{j}=\sum_{k=1}^{w}x_{j-w+k}/w = (x_{j-w+1}+\cdots+x_{j})/w,
特别地，如果针对时间序列的最后一个点，就可以得到：
SMA_{n} = \sum_{k=1}^{w}x_{n-w+k}/w = (x_{n-w+1}+\cdots+x_{n})/w.
因此，当前的实际值与光滑后所得到的值的差值就可以作为特征，i.e. SMA_{n}-x_{n} 就可以作为一个特征。然后根据不同的窗口长度 w\geq 1 就可以得到不同的特征值。
用和之前类似的方法，我们同样可以构造出一个神经网络算法来得到这个特征。



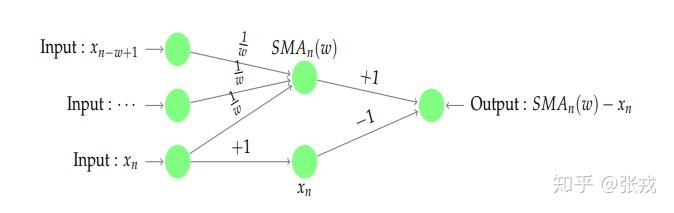
带权重的移动平均算法
带权重的移动平均算法指的是计算平均值的时候将不同的点带上不同的数值，i.e.
WMA_{j} = \sum_{k=1}^{w}k \cdot x_{j-w+k}/\sum_{k=1}^{w}k.
WMA_{n} = \sum_{k=1}^{w}k \cdot x_{n-w+k}/\sum_{k=1}^{w}k.
用和之前类似的方法，我们同样可以构造出一个神经网络算法来得到这个特征。



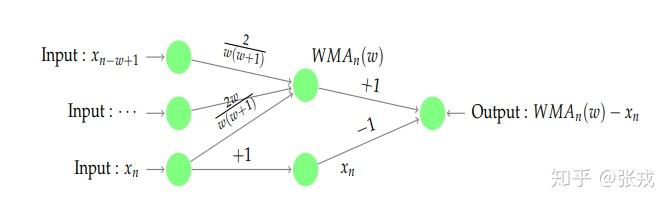
指数移动平均算法
指数移动平均算法指的是在已知时间序列的基础上进行加权操作，而权重的大小是呈指数衰减的。用公式来描述就是，已知时间序列 X_{n} = [x_{1},\cdots,x_{n}],  令
EWMA_{1}=x_{1},
EWMA_{j} = \alpha \cdot x_{j-1} + (1-\alpha)\cdot EWMA_{j-1}, \forall j\geq 1.
从定义上可以得到：
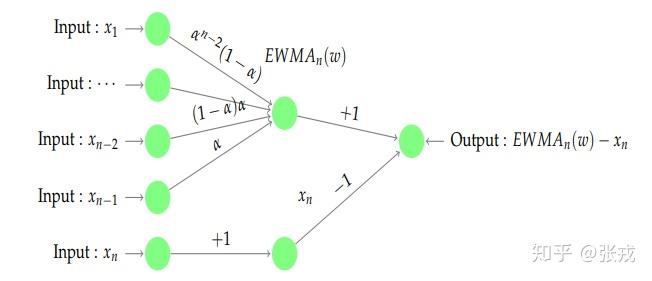
EWMA_{n} = \alpha[x_{n-1}+(1-\alpha)x_{n-2}+\cdots+(1-\alpha)^{k}x_{n-(k+1)}] + (1-\alpha)^{k+1}EWMA_{n-(k+1)}
\approx \alpha[x_{n-1}+(1-\alpha)x_{n-2}+\cdots+(1-\alpha)^{k}x_{n-(k+1)}]
因此，只需要构建一个加权求和，然后计算 EWMA_{n}-x_{n} 的取值就可以得到特征。所以，神经网络可以构建为如下形式：



深度学习与时间序列的周期性特征

在这里，时间序列的周期性特征就是指当前点与昨天同一个时刻，七天前同一个时刻的差值等指标。可以假设时间序列 X_{n} = [x_{week}, x_{yesterday}, x_{today}] 可以拆分成三个部分 x_{week}, x_{yesterday}, x_{today}, 分别是一周前的数据，昨天的数据，今天的数据，假设它们的长度都是 [n/3] ，最后一点都表示不同天但是同一个时刻的取值。所以，同环比特征
x_{today}[-1] - x_{yesterday}[-1] 与 x_{today}[-1] - x_{week}[-1] 都是可以通过神经网络构造出来。
mean(x_{today}) - mean(x_{yesterday})  与 mean(x_{today}) - mean(x_{week}) 这一类特征也可以构造出来。
有一些特征时用来计算是否高于历史一段时间的最大值，或者低于历史一段时间的最小值，在这里可以先构造  \max, \min  等函数，再计算两者的差值即可。例如，我们可以构造一个特征用于计算当前值是否高过昨天的峰值，以及超出的幅度是多少。用公式来表示那就是：
\max\{x_{today}[-1]-\max\{x_{yesterday}\}, 0\},
如果当前值  x_{today}[-1] 大于昨天的最大值，就返回它高出的幅度；否则就返回0。
也可以构造一个特征用于计算当前值是否低于一周前的最低值，以及低于的幅度是多少。用公式来表示那就是：
\min\{x_{today}[-1]-\min\{x_{week}\},0\},
如果当前值  x_{today}[-1]  小于一周前的最低值，就返回它低于的幅度；否则就返回0。
这两个特征只需要使用神经网络表示出 \max, \min, minus 激活函数使用 ReLU 即可。
深度学习与时间序列的分类特征

在时间序列的分类特征里面，有一种特征叫做值分布特征。假设时间序列的值域在  [0,1]  之内，值分布特征的意思是计算出一个时间序列  X_{n} = [x_{1},\cdots,x_{n}] 的取值在 [0,0.1), [0.1,0.2),\cdots,[0.9,1] 这十个桶的个数，进一步得到它们落入这十个桶的概率是多少。这一类特征可以通过之前所构造的 count 函数来生成。因此，分类特征也是可以通过构造神经网络来形成的。
深度学习与时间序列的特征总结

至此，我们已经证明，对于任意长度 n\geq 1 ，存在一个前馈神经网络，它的输入和输出分别是原始的时间序列与 Table 2 中的时间序列特征层。整体来看，
1. 存在多个前馈神经网络可以生成时间序列的特征；
2. 深度学习+时间序列异常检测可以实现端到端（End to End）的训练过程，也就是说：输入数据是归一化之后的原始数据（normalized raw data），输出的是两个标签（正常&异常），神经网络的权重可以通过大量数据集和目标函数训练出来。
3. 如果神经网络的输入是归一化之后的 raw data，输出是标签 1 或者 0。此时的前馈神经网络需要至少两个以上的隐藏层，才能够达到较好地提取特征的目的。
基于前馈神经网络的时间序列异常检测算法

通过前面的陈述，我们可以构造一个端到端（End to End）的前馈神经网络，意思就是说：前馈神经网络的输入层是原始的时间序列（归一化之后的数据），前馈神经网络的输出层是标签。
在这里，我们考虑的是三天数据的子序列，以 20180810 的 10:00am 为例，考虑当天历史三小时的数据（07:00-10:00），昨天 20180809 前后三小时的数据（07:00-13:00），再考虑一周前 20180803 前后三小时的数据（07:00-13:00）。这样就形成了一个子序列，总共有 903 个点。然后我们可以使用最大最小归一化获得神经网络的输入数据，而输出数据指的就是最后一个点是异常点（label = 0）还是正常（label = 1）。







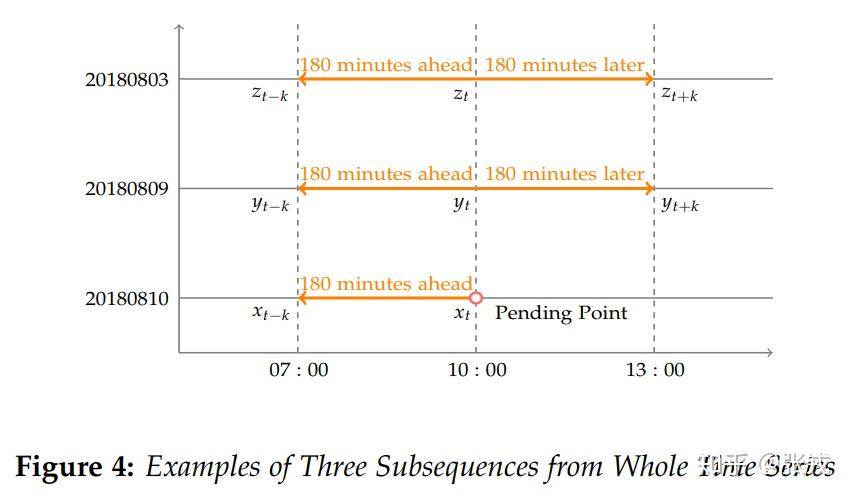
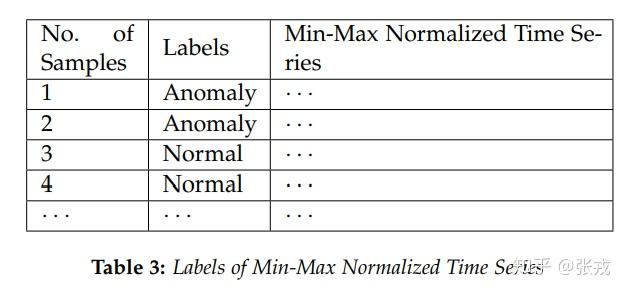
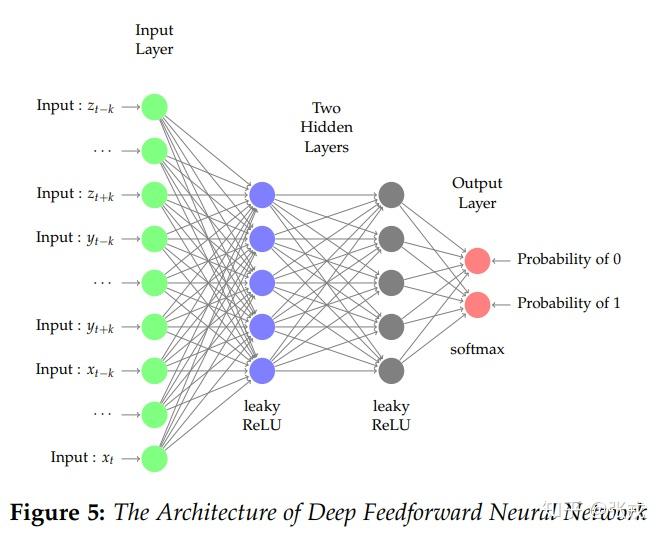
Figure 5 指出了前馈神经网络的结构图，输入层是归一化之后的时间序列原始数据，中间两层是隐藏层，输出层就是异常或者正常的概率值。而中间层的激活函数可以使用 ReLU 或者 Leaky ReLU，在这里我们通过实验发现 Leaky ReLU 的效果略好于 ReLU。而最后一层的激活函数使用的是 Softmax 函数，输出的两个概率值之和永远都是 1。
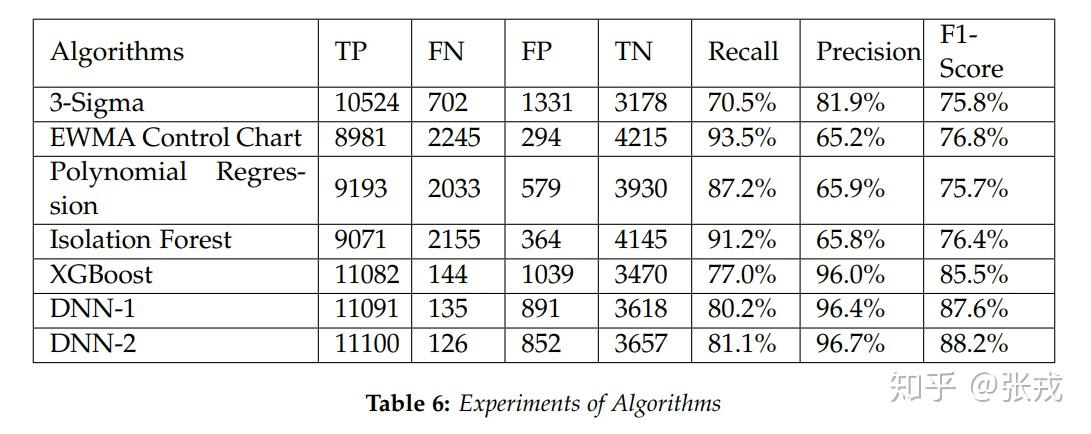
在这种神经网络结构下，神经网络的参数量级大约是 10 万量级，在这种情况下，使用少量的几百几千个样本几乎是无法训练出来的。在这里，我们使用了大约 10 万 的样本数据，才得到一个还不错的效果。在这里，我们使用 3-Sigma 算法，EWMA 控制图算法，多项式回归算法，孤立森林算法，XGBoost + 特征工程，前馈神经网络来进行算法的对比。通过数据的对比可以得到，XGBoost 与 DNN 其实差不多，都能够达到实际使用的上线标准。







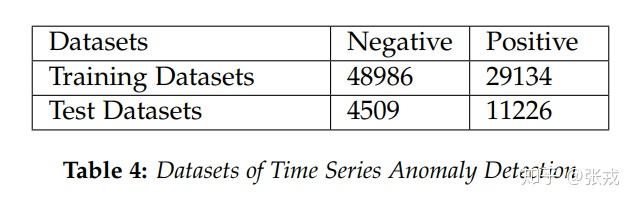
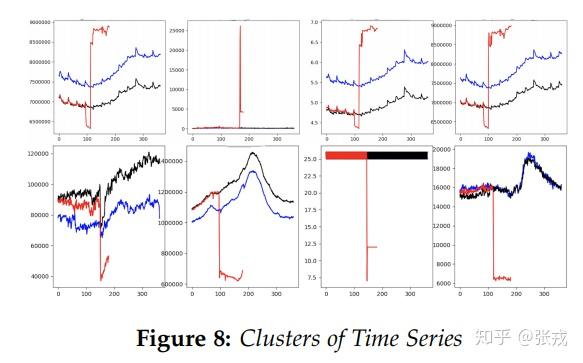
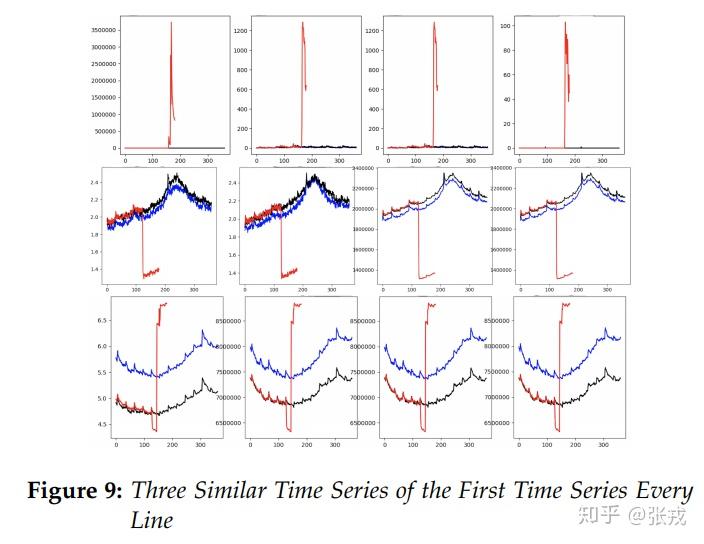
从深度学习的基础知识可以得到，CNN 的中间层可以用来提取图片的特征，因此，这里的前馈神经网络的隐藏层的输出同样可以作为时间序列的特征层。于是，我们通过实验，基于隐藏层的输出可以作为时间序列的隐藏特征，也就是所谓的 Time Series To Vector。通过 Time Series To Vector，我们可以既可以对时间序列进行聚类（KMeans），也可以对时间序列进行 Cosine 相似度的计算，进而得到同一类时间序列和相似的时间序列。





论文的主要结论

从本文的主要定理和实验效果来看，前馈神经网络是一个非常有效地可以用作时间序列异常检测的工具。本篇论文不仅提供了一个端到端的训练方法，并且不需要对时间序列进行特征工程的操作。从实验数据来看，使用前馈神经网络（feedforward neural network）可以得到与 XGBoost 差不多的效果。并且，前馈神经网络隐藏层的输出可以作为时间序列的隐藏特征（Time Series To Vector），使用 Cosine 相似度或者 KMeans 算法就可以对时间序列进行相似度的计算和聚类操作。在时间序列异常检测领域，使用特征工程 + 有监督算法的方法论比较多，而使用端到端的训练方法，也就是前馈神经网络的方法应该还是相对较少的。因此，端到端的前馈神经网络算法应该是本文的方法与其他方法论的最大不同点。
参考文献

• 《企业级 AIOps 实施建议》白皮书-V0.6 版本
  
• 《腾讯运维的AI实践》--- 2018年4月 GOPS 全球运维大会
  
• 《Feedforward Neural Network for Time Series Anomaly Detection》，Arxiv，2018年12月18日
  
• Github：https://github.com/Tencent/Metis
  

原文地址：https://zhuanlan.zhihu.com/p/54471673