如何形象地理解统计学中的各种检验方法？

莺歌燕舞 · 发表于 2024-12-26 12:09

登陆有奖并可浏览互动！

您需要登录才可以下载或查看，没有账号？立即注册

×

查了一下常用的几种检验方法，什么T检验、U检验、卡方检验等等，但是由于非专业看不明白，能否请大神深入浅出，举例讲解，拜托。
原文地址：https://www.zhihu.com/question/63678946

继续前进 · 发表于 2024-12-26 12:10

所有统计检验的本质都是三步。
1.猜测数据结构
2.抽样
3.计算抽到的样本，在猜想数据结构中的理论概率，判断能都否接受（是否保留对数据结构的猜测）

比如，我想看看一个班级50人的性别分布
1. 猜测数据结构：49男，1女
2. 抽样：调取两名学生的档案，看看性别
3. 计算理论概率可能有：
（1）两男概率： $\frac{C_{49}^{2}}{C_{50}^{2}}=\frac{48}{50}=0.96$
（2）一男一女概率： $\frac{C_{49}^{1}}{C_{50}^{2}}=\frac{49}{50*49/2}=0.04$
（3）两女概率： $0$
在我第二步抽样的结果来看：
（1）如果我正好抽中了两个男生，理论上的可能性为96%，那有这个结果不出乎意料，基本符合我的猜想
（2）如果我抽中了一男一女，就有点儿值得怀疑了。这么小概率的事件（仅4%的可能性），怎么一次就让我抽中了呢？
（3）如果我抽中了两女。这是理论上的「不可能」事件，唯一合理的解释，我第一步的数据结构猜错了，至少是48男，2女的结构。

再比如，我想看看一只股票的收益率分布
1. 猜测数据结构：正态分布，服从 $N（0，1）$
2. 抽样：回顾历史，看看某一天的收益率
3. 计算理论概率可能有：
（1）在-1到1之间的概率： $\approx0.68$
（2）在-2到2之间的概率： $\approx0.95$
（3）在-3到3之间的概率： $\approx0.99$
这意味着，如果我随机抽样一天的收益率，99%的可能都在亏三倍和赚三倍之间。如果，我恰好抽样发现收益率超过300%，我就有理由怀疑，收益率的数据结构不是 $N（0，1）$ 的正态分布。

在这个基本的统计检验思想之外，其实还有很多值得讨论的有趣问题。
1.数据结构都有什么样的呢？
这个问题的答案几乎就是统计学的发展简史。
最直观的结构就是二项分布，有或没有，是或不是；多次的二项分布就构成了泊松分布（统计「是」的个数与「否」的个数）；连续的泊松分布就导出来正态分布；正态分布平方和就是卡方分布；正态分布比卡方分布就是T分布；卡方分布比另一个卡方分布就是F分布，等等。

统计分布关系。图片来源：https://www.math.wm.edu/~leemis/chart/UDR/UDR.html

这就是题主举例的几种常见的统计分布检验，但是他们的本质与（49男，1女）例子没有什么本质上的不同。只不过猜测的数据结构不同，导致抽样的理论概率有所变化而已。
2.可以不猜测数据结构嘛？
可以。
事实上，现实中的数据恰好符合某种典型的数据结构才是特例。那么，没有标准的数据结构形状，要如何做统计检验呢？
回归最直观的频率派。我可以不知道什么是正态分布，我只知道，过去三年的交易日中，有超过600天，单只股票的收益率在-300%和+300%之间，那么如果我看到某天某只股票的收益率是400%（太低频了），那天或那只股票一定有点儿与众不同的地方。这也就是半参估计甚至非参估计的思想。
3. 单次抽样是不是太看运气了？
是的。
某件事情发生的概率很小，也不代表这件事情，就是不可能的。有可能某个人运气好，恰好在抽样的时候抽中了小概率事件，这种情况是不可避免。你只能在心里设定一个标准，究竟是5%算小概率事件，还是1%算小概率事件？然后在此基础之上来判断是否拒绝你对原始数据结构的猜测。经济学上常用5%作为判断的临界点，但这个标准也只是约定俗成而已。

————————————
学无止境，永保好奇~

检验医师 · 发表于 2024-12-26 12:11

统计在许多领域都有应用，在日常生活中我们也常常接触到各种统计数据，比如，媒体报道中使用的统计数据和图表等，下面我们具体展开说说：

可视化图形篇

1.小提琴图
不同地区的身高问题
SPSSAU：小提琴图如何分析？2.核密度图
不同性别的身高分布
SPSSAU：核密度案例如何分析？3.气泡图
用气泡大小展示可支配收入情况
SPSSAU：气泡图如何做？4.组合图
展示GDP及其增长率情况
SPSSAU：组合图该怎么分析？更多资料请参考：SPSSAU官网。

问卷研究篇

1.信度
答问卷的人是否认真回答量表题项
SPSSAU：信度案例如何分析？2.效度
测量问卷题是否准确有效
SPSSAU：简单实用！一文掌握效度分析所有知识点！3.中介作用
研究职业压力对工作满意度影响工作绩效的过程是否起到了中介作用。
SPSSAU：中介作用如何操作？4.调节作用
研究工作绩效在工作满意度与离职意愿之间，是否具有调节作用。
SPSSAU：如何分析调节作用？更多资料请参考：SPSSAU官网。

医学统计篇

1.卡方检验
不同性别的人群，使用理财产品的情况是否有差别。
SPSSAU：全流程总结卡方检验，帮你理清分析思路2.Cox回归
某大型超市推出了注册会员领优惠券活动，自活动开始现在抽取了部分用户数据，希望通过Cox回归了解客户流失情况，以及会员优惠券和顾客年龄对客户流失有没有影响关系。
SPSSAU：客户流失快？Cox回归帮你寻找真相3.游程检验
当前共有30位选手参加比赛，每位评委针对选手进行打分，现在想研究出场顺序对选手得分是否有影响，选择游程检验进行分析。
SPSSAU：数据随机性，如何利用游程检验来检测？4.极差分析
研究大豆出油率分别与3个因素的关系情况，分别是萃取液，温度和处理时间。需要设计一个三因素三水平的正交试验表，并收集试验数据后进行分析，希望找出3个因素时各水平的最佳大豆出油率组合。
SPSSAU：实用干货！正交试验设计及极差分析步骤总结！5.OR值
以吸烟者和罹患肺癌的风险为例。暴露组（吸烟者）中有20人患上肺癌（阳性），80人没有患上肺癌（阴性）；而非暴露组（非吸烟者）中，有5人患上肺癌，95人没有患上肺癌。现希望分析暴露与疾病风险程度的关系（OR值），并且可查看发病率比例情况（RR值）。
SPSSAU：如何一键计算OR值？更多资料请参考：SPSSAU官网。

计量经济学篇

1.OLS回归
研究高管信息以及企业规模资产对于研发投入的影响。
SPSSAU：OLS回归案例分析2.分位数回归
研究一项雇员工资影响因素，影响因素X共有三项，分别是‘‘起始工资’，‘受雇月数’和‘受教育年限’。因变量Y为当前工资。
SPSSAU：分位数回归案例怎么分析？3.倾向得分匹配
希望研究是否读过研究生，对于年收入的影响情况。其他变量还包括父母学历，父母是否从事教育相关职业等。
SPSSAU：一文了解什么是倾向得分匹配PSM？4.DID差分
有50个地区分别11年（2010~2020）的数据（共计50*11=550行）。50个地区可分为两类地区A和B(分别均为25个)，在2016年A类地区没有开通高铁，B类地区开通高铁。那么开通高铁对于GDP的影响情况。
SPSSAU：多期数据DID操作5.面板模型
9个地区的11年的数据作为案例数据，数据中包括X1(城乡居民年末储蓄存款), X2(年末常住人口), X3(城镇化率), X4(教育支出)共4个自变量，因变量为GDP。
SPSSAU：面板模型回归操作指南，适合初学者！6.RDD断点
例研究是否民主党获选对于联邦支出的影响。
SPSSAU：RDD断点回归案例怎么分析？更多资料请参考：SPSSAU官网。

生活实际篇

1.熵值法
对各企业的财务状况进行综合评价分析。
SPSSAU：手把手教你用熵值法计算权重2.因子分析
抽取了150名员工的的绩效考核情况，共考察8项指标分别是工作效率、工作成果、创新能力、人际关系、合作意识、出勤情况、工作积极性、学习能力。希望通过分析，了解每个员工的绩效情况。
SPSSAU：如何利用因子分析考核员工绩效？3.主成分分析
选取反映区域经济发展水平的7个指标，对我国15个副省级城市的经济发展水平进行综合评价研究。
SPSSAU：手把手教你做主成分分析（附数据）4.聚类分析
案例采用著名的鸢尾花iris数据集，按鸢尾花的三个类别（刚毛，变色，佛吉尼亚），每一类50株，共测得150株鸢尾花的花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性数据做聚类分析。
SPSSAU：手把手教你做K均值聚类分析（附操作数据）5.PLS回归
研究身体特征指标分别是体重X1、腰围X2和脉博X3对于训练指标单杠Y1、弯曲Y2和跳高Y3的影响关系。
SPSSAU：PLS回归是个啥？与线性回归有什么区别？更多资料请参考：SPSSAU官网。
<hr/>SPSSAU

大力水手 · 发表于 2024-12-26 12:12

数据统计检验基础

一、变量类型
数据统计时使用的数据是对变量的测量。根据实际情况，需要检测的变量类型分为数值型数据（Scale）和分类型数据（Categorical）。数值型数据包括连续型数据（Continuous，如身高、距离等）和非连续型数据（Discrete，如个数）。分类型数据包括定序型数据（Ordinal，如对某事物的评价：好、一般、不好）、定类型数据（Nominal，如性别）。

二、统计数据的呈现方式。
数值型数据通常用平均值（mean）、中值（median）、最大值、最小值、标准差（SD）、标准误（SEM）、四分位等表示，用于体现数据的分布情况。分类型数据中的定序型数据可以用中值和四分位表示。定类型数据直接用数据展示。

数据的图形表现方式：饼图、柱状图、累积柱状图、直方图、散点图、箱线图、拆线图等。

三、统计检验方法的选择
1、数值型数据
对于数值型数据，有参数检验和非参数检验两类方法。参数检验比非参数检验准确度高，但有使用条件，如数据符合正态分布，不同数组之间的方差无显著差异（即方差齐性）。非参数检验对是否符合正态分布，方差齐性无要求。
2、分类型数据
分类型数据中的定序型数据，使用非参数检验。定类型数据可使用卡方检验（Chi-squared，也叫联表检验）或Fisher检验。对于2x2联表卡方检验，要求每个格子中的理论频数≥5，总样本量≥40。如果不符合要求，使用Fisher检验。对于RxC联表（R行，C列），使用卡方检验的条件是理论频数小于5的格子不能超过1/5，且不能有小于1的理论频数。
3、相关性检验
两组连续变化的数据是否存在相关性，可使用Pearson’s Correlation Coefficient或Spearman’s Correlation Coefficient。前者为参数检验，后者是非参数检验。

四、常用数值型数据的检验
1、检验数据是否符合正态分布
常用方法为Kolmogorov-Smirnov test (K-S检验)和绘制QQ图。在Prims9中可使用Normality and Lognormality Tests进行。K-S检验存在显著差异时，不符合正态分布，无差异时，符合正态分布。QQ图中数据点分布接近45°直线时，符合预期分布。

2、检验方差齐性
方法有F-test, Bartlett’s test, Levene’s test三种。F-test用于比较符合正态分布的2组数据，可在excel中用F.test函数检测。Levene’s test用于比较不符合正态分布的2组及以上数据。Bartlett’s test用于比较符合正态分布的3组及以上数据。
3、参数检验
满足正态分布和方差齐性两个条件时，使用参数检验。参数检验方法有t检验或ANOVA检验。t检验用于比较两组数据的均值是否无差异，有paired t-test（成组样本t检验）和unpaired t-test（独立样本t检验）。paired t-test适用于成组样本，如同一样品处理前和处理后获得的数据，两组数据的样本大小一样，成对存在。unpaired t-test用于两组独立样本，样本大小可以不同。ANOVA用于比较3组或以上数据之间是否存在差异。ANOVA有One-way、Two-way和Three-way，使用哪一种取决于变量的个数，对应变量数分别是1、2和3。
注意（1）：数据展示可以用平均值±标准差SD，或平均值±标准误SEM表示。选择哪一种，取决于需要。SD用于显示数据分散程度，不随样本大小变化，SEM表示的是样本平均值与总体平均值的差异，其大小与样本量有关，样本越大，数值越小。可以理解为不同样本的平均值的标准差。换算关系估算为SEM=SD/(√n)，其中n为样本大小。【注意N的大小写意义不同，不可随意使用。N表示总体样本量，n表示取样样本量，是不一样的！一般情况下用小n】SD和SEM单位一样。生物学研究中SD和SEM经常被认为可以互换，但其实不准确。一般情况下，需要展示数据均一程度，使用SD。通常也可使用散点图显示实际数据，同时标上平均值和SD。如果对同一批次多个样本进行测量，每次测量有重复，那么不同样本的平均值再取平均作为最终均值，此时这些平均值的标准差即SEM。
注意（2）：统计检验时，单尾和双尾的选择。当两组数据之间的差异是可高可低时，使用双尾。如果因实际情况，其中一组只可能比另一组高或低时，使用单尾。
注意（3）：对于样本量很大时，样本间的统计差异（p值）会很低。此时，通过p值表征数据差异性的实际意义就存在问题。因为只要样本量够大，肯定显著。有人曾提出N<30时，使用t检验，N>30时使用z检验。也有人认为t检验适用所有情况，N很大时，p值一定会很低，这种差异是真实存在的。Cohen提出使用Effect size代替p值。Effect size=(比较组平均值-对照组平均值)/对照组SD。Effect size越大，差异越大（如>0.5）。Effect size和样本数量无关。
4、非参数检验
不符合正态分布或方差不齐，或不能确定是否符合条件时，使用非参数检验。两组数据的非参数检验使用Mann-Whitney U检验（也叫Wilcoxon rank-sum 检验）或Wilcoxon signed rank检验。Mann-Whitney U用于比较独立的两组数据，对应参数检验中的unpaired t-test。Wilcoxon signed rank用于比较成对的两组数据，对应参数检验中的paired t-test。三组独立数据使用Kruskal-Wallis检验，对应参数检验中的One-way ANOVA。
五、常用检验方法汇总

参考文献：https://www.statstutor.ac.uk/resources/uploaded/tutorsquickguidetostatistics.pdf

继续前进 · 发表于 2024-12-26 12:12

你好，这篇文章比较深入浅出给出很多种检验方法，望参考！
前言

估计和检验是统计学上最常见的两种分析手段。参数估计主要两大类为点估计和区间估计，这里面具体涉及的方法很多。本文主要描述的内容是关于检验方面的。假设检验的着重点在于检验参数的取值是否等于某个目标值。

<hr/>一：假设检验的背景知识简介

两类思想

小概率事件：小概率事件是指在一次独立实验中几乎不可能发生的事件，如果在我们的假设下出现了小概率事件，那么就可以认为我们的假设是错误的，
反证法思想：先假设我们提出的假设是正确的，然后在该条件下检验观测到的事件是不是小概率事件。如果是，那么就可以否定我们的假设；否则，我们就无法否定。

假设检验步骤总结

先根据实际情况的要求提出一个论断，称为原假设或零假设，记为 $H_0$ 。同时提出一个互为反命题的备择假设，记为 $H_1$ ，
在 $H_0$ 正确的条件下，求出样本数据出现的概率，看已知的样本是不是小概率事件，
如果样本是小概率事件，那么就认为原假设错误，即拒绝原假设，否则就是接受原假设。
对于原假设和备择假设假设的选择原则：（1）.原假设应该是受保护的，不能轻易被拒绝；（2）.备择假设是检验者所希望的结果；（3）.等号永远出现在原假设中。

两类错误

第一类错误：即弃真错误。尽管小概率事件很难发生，但毕竟概率不为0，也许原假设是正确的，但根据小概率事件原则，我们拒绝了原假设，犯第一类错误的概率为 $\alpha$ ，
第二类错误：即取伪错误。也就是说，在假设检验中我们没有拒绝原本是错误的原假设，因为有时候原假设尽管是错误的，但非常接近真实值，犯第二类错误的概率为 $\beta$ ，
错误权衡：如果我们想要降低 $\alpha$ 的概率，也就是意味着提高拒绝条件，使得原假设不那么容易被拒绝，但与此同时，错误的原假设也不容易被拒绝，相当于提高了 $\beta$ 值，所以二者不可能同时降低的。一般来说我们是控制 $\alpha$ 而放任 $\beta$ 。

显著性水平 $\alpha$ 与 $p$ 值

为了控制 $\alpha$ ，我们往往将 $\alpha$ 的值固定，用条件概率表示为：
$P\left( 拒绝H_0|H_0为真 \right)\leq\alpha$ ，对于 $\alpha$ 取值我们有 $\alpha$ =0.1，0.05或者0.01。
关于 $p$ 值的解释，这里主要是对“更极端”事件出现的概率进行量化。比如原假设总体均值为10，样本的均值为9，样本均值原假设的差即为-1。那么“更极端”的情况就是指均值和10的差大于1或者小于-1的样本。我们于是把所得到的样本或者更极端的情况出现的概率叫做 $p$ 值。

确定小概率事件

判定一个事件是否为小概率事件的基本原则就是：当 $p$ 值小于等于 $\alpha$ 时，我们的样本为小概率事件，而对于这两个值的比较，我们可以采用临界值检验法和显著性检验法！

临界值检验法：简单来说就是根据样本构造合适的统计量后，根据 $\alpha$ 和统计量所服从的概率分布求得临界值，一般临界值都满足一个特性，那就是 $p=\alpha$ ，求得临界值后，可以将统计量与该临界值进行比较。如果统计量与原假设的偏差大于等于临界值与原假设的偏差，那么当前样本就与临界值一样极端或者更极端，其 $p$ 值也就会小于等于 $\alpha$ ，所以我们就认为当前样本为小概率事件，从而拒绝原假设。
显著性检验法：开始同样构建一个用于检验的统计量，与临界值法不同的是，我们直接根据原假设和统计量的概率分布求解其 $p$ 值，然后将 $p$ 值与 $\alpha$ 进行比较，从而判定样本是否为小概率事件。

二：参数检验之 $t$ 检验（主要用于样本含量较小（例如n < 30），总体标准差σ未知的正态分布）

所谓参数检验，即构造的统计量或者总体分布服从一定的概率分布的情况下对总体参数（如均值、方差）推断。

单样本 $t$ 检验：

在总体服从正态分布 $N\left( \mu,\sigma^2 \right)$ 的情况下，比较总体均值 $\mu$ 是否与指定的检验值 $\mu_0$ 存在显著性差异，原假设（双尾，如果是单尾原假设，即 $\mu_0\geq\mu$ 或 $\mu_0\leq\mu$ ，备择假设为互逆命题）为 $H_0：\mu=\mu_0$ 。如果样本容量为 $n$ ，样本均值为 $\bar{X}$ ，在原假设成立的条件下，我们构建如下 $t$ 检验统计量：
$t=\frac{\bar{X}-\mu_0}{s/\sqrt{n}}\sim t(n-1)$ 其中 $s=\sqrt{\frac{1}{n-1}\sum_{i}^{n}{\left( x_i-\bar{x} \right)^2}}$ 为样本标准差。
得到统计量值后，我们便可根据 $t$ 分布的分布函数计算出 $p$ 值并与显著性水平 $\alpha$ 进行比较，或者与显著性水平 $\alpha$ 下的临界值进行比较。
我们用Python实现这一过程：
import numpy as np
from scipy import stats
arr = np.array([10.1,10,9.8,10.5,9.5,10.1,9.9,10.2,10.3,9.9])
test_res = stats.ttest_1samp(arr,0)#原假设是收益率均值为0
##编写统计量值计算公式
mu = arr.mean()
mu = mu - 0
t = mu / (np.std(arr,ddof=1) / np.sqrt(len(arr)))
print(test_res)
print(&#39;公式得到的t统计量值：&#39;,t)
if test_res[1] < 0.05:
print(&#39;\033[1;32m原假设是收益率均值为0，由于p值为%s，小于显著性水平a=0.05，所以拒绝原假设，即收益率均值为0假设不成立！\033[0m&#39;%test_res[1])
else:
print(&#39;\033[1;31m原假设是收益率均值为0，由于p值为%s，大于等于显著性水平a=0.05，所以接受原假设，即收益率均值为0假设成立！\033[0m&#39; % test_res[1])

##根据概率分布手动计算p值（双尾）
p_value = (1 - stats.t.cdf(t, df=len(arr)-1)) * 2
print(&#39;手动计算P值：&#39;,p_value)

独立样本 $t$ 检验：

用于检验两个服从正态分布的总体均值是否存在显著性差异，假设两个总体分布分别为
$N\left( \mu_1,\sigma_1^2 \right)$ 和 $N\left( \mu_2,\sigma_2^2 \right)$ ，则原假设为 $H_0:\mu_1=\mu_2$ ，那么由正态分布可加性
$(x_1+x_2+...+x_n)\sim N\left( n\mu,n\sigma^2 \right)$ ，则 $\bar{x}\sim N\left( \mu,\frac{\sigma^2}{n} \right)$ ，则对于两独立样本有
$\bar{x_1}-\bar{x_2}\sim N\left( \mu_1-\mu_2,\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2} \right)$ ，简化其中推导我们直接给出其检验统计量为
$\frac{(\bar{x_1}-\bar{x_2})-(\mu_1-\mu_2)}{\sqrt{s_p\left( \frac{1}{n_1}+\frac{1}{n_2} \right)}}\sim t(n_1+n_2-2)$ ，
这里的 $s_p=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}$ 为混合标准差。
同上“单样本方法”计算相应 $p$ 值。
我们用Python实现这一过程：
arr1 = np.array([5,4,2,3,4,5,6,7,3])
arr2 = np.array([2,3,4,2,3,4])##两样本长度不必相等！！
res = stats.ttest_ind(arr1,arr2)
print(res)

配对样本 $t$ 检验：

当两样本并不互相独立时候，我们可以使用配对样本 $t$ 检验对两个总体的均值差异进行检验。比如研究夫妻之间的人均消费差异，因为夫妻双方的人均消费水平并不是独立的，这时候我们只需要稍变变形一下，即用丈夫的消费水平减去妻子的消费水平的差值做单样本 $t$ 检验即可。则建立的原假设
$H_0:d=\mu_1-\mu_2=0$ ，其检验统计量为： $t=\frac{\bar{d}}{s_d/\sqrt{n}}\sim t(n-1)$ ，这里要说明 $\bar{d}$ 为配对样本中各元素对应的差值， $s_d$ 为差值的标准差， $n$ 为配对数。
同上“单样本方法”计算相应 $p$ 值。
我们用Python实现这一过程：
arr1 = np.array([5,4,2,3,4,5,6,7,3])##注意这时候的两个向量长度要求一致！！
arr2 = np.array([2,3,4,2,3,4,3,9,10])
res = stats.ttest_rel(arr1,arr2)
print(res)三：参数检验之 $z$ 检验（主要用于大样本（例如n > 30），总体标准差σ已知的正态分布）

由于 $z$ 检验和 $t$ 检验原理很像，这里我们将简单介绍下其原理。

样本容量越大，样本标准差接近总体标准差！

对于总体方差已知的样本情况，对单样本 $z$ 检验，我们有统计量 $z=\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}$ ,一般原假设（双尾）还是设为 $H_0:\mu=\mu_0$ ，双样本检测原理跟同理 $t$ 检验。
我们简单用代码运用此方法：
import statsmodels.stats.weightstats as sw
arr1 = [23,36,42,34,39,34,35,42,53,28,49,39,46,45,39,38,45,27,43,54,36,34,48,36,47,44,48,45,44,33,24,40,50,32,39,31]
arr2 = [41, 34, 36, 32, 32, 35, 33, 31, 35, 34,37, 34, 31, 36, 37, 34, 33, 37, 33, 38,38, 37, 34, 36, 36, 31, 33, 36, 37, 35,33, 34, 33, 35, 34, 34, 34, 35, 35, 34]
###返回的元组形式，第一个值是统计量的值，第二个值是p值
print(sw.ztest(arr1, value=39, alternative=&#39;two-sided&#39;))##其中value单样本时候，是样本假设的均值，默认双尾检验
print(sw.ztest(arr1,arr2, value=0))##其中value单样本时候，是两样本假设的均值之差
###根据概率分布求解p（双尾）
p_value = (1 - stats.norm.cdf(z检验统计量值)) * 2四：参数检验之方差分析

方差分析主要研究的是一个因子对反应变量的影响。比如分析食品行和金融行业的股票收益率的差异，如果发现这两个行业的股票收益率有显著差异，则可有一下结论：行业是影响股票收益率的一个重要因素。
方差分析的目的在于分析因子对反应变量的有无显著影响，亦即因子的不同水平下反应变量的均值是否有显著差异。若因子水平对反应变量无影响，则不同因子水平下反应变量的均值是相同的，这也就是方差分析的原假设。
方差分析要满足以下两点：

样本是从服从正态分布的总体中独立抽取出来的，
不同反应变量的总体方差是大致相同的（方差一致性）。

接下来，我们简单概括一下方差分析的一般步骤：

根据感兴趣的因子的不同取值水平，将反应变量分为 $M$ 个组，
提出原假设，即 $H_0：$ 因子对于反应变量均值没有影响；备择假设 $H_1:$ 因子对于反应变量均值有影响，
求出样本数据中每组样本的平均值和全体样本的平均值，算出组内均方差MSF和组间均方差MSE，
构建统计量 $\varphi=\frac{MSF}{MSE}\sim F(M-1,N-M)$ ，其中 $F$ 为 $F$ 分布，
由显著性水平 $\alpha$ 的取值，查 $F$ 分布表的临界值 $F_\alpha(M-1,N-M)$ 来判断是接受还是拒绝原假设。

单因素方差分析

比如我们列举的例子就是关于行业是否是影响股票收益率的一个重要因素。
from statsmodels.formula.api import ols
import statsmodels.stats.anova as no
import pandas as pd
return_ls = [0.57298,0.82757,0.33648,0.64532,0.47798,0.25123,0.00256,0.01125,0.75658,0.05654,0.95765,0.87851,0.99856,0.00245]
industry_ls = [&#39;货币金融服务业&#39;,&#39;房地产行业&#39;,&#39;医药制造业&#39;,&#39;房地产行业&#39;,&#39;房地产行业&#39;,&#39;游戏业&#39;,&#39;农业&#39;,&#39;电影业&#39;,&#39;服务业&#39;,&#39;交通业&#39;,&#39;房地产行业&#39;,&#39;房地产行业&#39;,&#39;房地产行业&#39;,&#39;农业&#39;]
df1 = pd.DataFrame([return_ls,industry_ls],index=[&#39;Return&#39;,&#39;Industry&#39;]).T
data_new1 = df1.dropna()
data_new1[&#39;Return&#39;] = data_new1[&#39;Return&#39;].apply(pd.to_numeric)#强行转化为数值
model1 = ols(&#39;Return ~ C(Industry)&#39;,data_new1).fit()
table1 = no.anova_lm(model1)
print(table1)

图1

由上图图1 $p$ 值我们发现，对于因变量收益率，自变量行业确实是对因变量有显著影响的。

多因素方差分析（独立）

顾名思义，研究多个因子是否对因变量有重要影响，且每个因子影响对因变量的影响方向和程度是不一样的。
edu_ls = [13,18,3,5,8,12,3,8,12,15]
marr_ls = [&#39;y&#39;,&#39;y&#39;,&#39;n&#39;,&#39;n&#39;,&#39;n&#39;,&#39;n&#39;,&#39;y&#39;,&#39;n&#39;,&#39;n&#39;,&#39;y&#39;]
ear_ls = [77005,85212,5264,10222,20013,31212,6451,18221,45613,56872]
df2 = pd.DataFrame([edu_ls,marr_ls,ear_ls],index=[&#39;education&#39;,&#39;married&#39;,&#39;earnings&#39;]).T
data_new2 = df2.dropna()
data_new2[&#39;earnings&#39;] = data_new2[&#39;earnings&#39;].apply(pd.to_numeric)
model2 = ols(&#39;earnings ~ C(education)+C(married)&#39;,data_new2).fit()
table2 = no.anova_lm(model2)
print(table2)

图2

由上图图2我们发现，当研究两个变量是否对收入有影响时，我们发现教育和是否结婚影响程度是不一样的，教育是有显著影响的，而是否结婚是没有显著影响的。

析因素方差分析（非独立）

析因方差分析与多元素方差分析差不多，仅多了一个因子乘项。比如，在上面的例子中，我们可以添加married与education的乘项，以检验这两者对收入的影响是否与另一个因子水平有关。
model3 = ols(&#39;earnings ~ C(education)*C(married)&#39;,data_new2).fit()
table3 = no.anova_lm(model3)
print(table3)

图3

由上面图3我们发现，第3个 $p$ 值等于0.05<0.5，即结果不显著，所以婚姻状况和受教育水平对收入的影响并不依赖于另一者的水平。
五：非参数检验之卡方检验

卡方检验（慎与跟卡方分布概念混淆）是一种用途很广的计数资料的假设检验方法。属于非参数检验，主要是比较两个及两个以上样本率（构成比）以及两个分类变量的关联性分析。根本思想在于比较理论频数和实际频数的吻合程度或者拟合优度问题。

接下来，我们简单概括一下卡方检验（特指拟合优度）的一般步骤：

建立独立样本联表，建立原假设 $H_0:$ 比如不吃晚饭对体重下降没有影响，或者喝牛奶对身体恢复没影响等等，

	身体恢复慢	身体恢复快	总数
喝牛奶	15	95	110
不喝牛奶	85	5	90
总数	100	100	200

2. 根据概率频次对四方联表进行理论值频数计算，

	身体恢复慢	身体恢复快	总数
喝牛奶	110/200*100=55	110/200*100=55	110
不喝牛奶	90/200*100=45	90/200*100=45	90
总数	100	100	200

3. 卡方检验统计量公式： $\chi^2=\sum_{i}^{k}{\frac{\left( f_o-np_i \right)^2}{np_i}}$ ，这里的 $k$ 就是就是总体样本分为 $k$ 块，也就是4， $n=$ 200。根据拟合优度公式有 $\chi^2$ = $\frac{\left( 95-55 \right)^2}{55}+\frac{\left( 15-55 \right)^2}{55}+\frac{\left( 85-45 \right)^2}{45}+\frac{\left( 5-45 \right)^2}{45}=129.3$
4. 根据自由度计算公式： $v=(行数-1)(列数-1)$ 以及 $\chi^2$ 临界表、拟合优度值，我们可查到 $p$ ，
5. 根据 $p$ 值的取值的大小来确定是否拒绝原假设。
我们用直接调用Python里的方法走一遍上面的过程。
from scipy.stats import chi2_contingency

df = pd.DataFrame({
&#39;medical&#39;:[&#39;A&#39;,&#39;A&#39;,&#39;B&#39;,&#39;B&#39;,&#39;C&#39;,&#39;C&#39;],
&#39;cured&#39;:[1,0,1,0,1,0],
&#39;count&#39;:[1800,200,600,1200,500,200]
})
print(&#39;\033[1;31m原始表：\033[0m&#39;)
print(df)
cross_tab = pd.pivot_table(data=df,values=&#39;count&#39;,index=&#39;medical&#39;,columns=&#39;cured&#39;,margins=True,aggfunc=np.sum)
print(&#39;\033[1;32m联表：\033[0m&#39;)
print(cross_tab)
kf = chi2_contingency(cross_tab)
print(&#39;chisq-statistic=%.2f, p-value=%.6f, df=%s expected_frep=%s&#39;%kf)

图4

从上图图4的 $p$ 值，我们可以发现不同药对治疗效果是有关系的。

PS：卡方检验的结果非常受数据量级的影响，实际运用中要注意！！！

六：非参数检验之Kruskal-Wallis检验

在实际生产中，经常比较多组独立数据均值（或者分布）之间的差异性，然而实际数据很难符合正态性，基本都是偏态性，这时很难用参数检验进行分析。作为对样本分布没有太大要求的Kruskal-Wallis（简称克氏）检验，它是一个将两个独立样本Wilcoxon(Mann-Whitney)推广到3个或者更多组的检验。
接下来，我们简单概括一下Kruskal-Wallis检验的一般步骤

对于分布是否相同的检验的原假设可以设为 $H_0:F_1(x)=F_2(x)=...=F_k(x)$ ，这里的 $k$ 为是独立样本的个数， $F$ 是分布函数的意思，那么备择假设 $H_1:$ $F$ 中至少两个不相等，对于位置参数（均值、中位数等）的原假设 $H_0:\theta_1=\theta_2=...=\theta_k$ ，备择假设同理，

2. 构造检验统计量 $H=\frac{12}{N(N+1)}\sum_{i}^{k}{n_i\left(\bar{R}_j-\bar{R} \right)^2}$ ，这里的统计量涉及的参数比较多，有秩的概念、总样本的概念等，我们这不详细介绍，主要介绍检验用法，有兴趣的可以参考这，
4.1 Kruskal-Wallis 秩和检验3. 作出决策，对于大样本和小样本的统计量分布查表是不同的，大样本下近似 $H$ 近似服从 $\chi^2(k-1)$ ，小样本下可直接查表得到，通过决策值或者 $p$ 值判定是否拒绝或接受原假设。
我们以实际例子作为联系，研究不同的药对咳嗽的治疗是否不同，
from scipy import stats

##服用不同药情况下咳嗽人群阶段治愈数
medicine_a = [80,203,236,252,284,368,457,393]
medicine_b = [133,180,100,160]
medicine_c = [156,295,320,448,465,481,885]
medicine_d = [194,214,272,330,386,475]
df = pd.DataFrame([medicine_a,medicine_b,medicine_c,medicine_d],index=[&#39;medinine_a&#39;,&#39;medinine_b&#39;,&#39;medinine_c&#39;,&#39;medinine_d&#39;]).T
test_res = stats.kruskal(df[&#39;medinine_a&#39;].dropna(),df[&#39;medinine_b&#39;].dropna(),df[&#39;medinine_c&#39;].dropna(),df[&#39;medinine_d&#39;].dropna())
print(test_res)

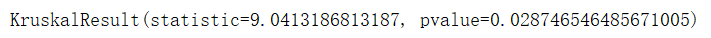
图5

由上图5我们根据 $p$ 值发现，不同药对咳嗽的治疗是有不同作用的。
另外，K-W检验对应于参数检验的方法是方差分析，即研究因子在不同水平下对反应变量均值是否有显著影响，那么假设以上数据满足方差齐次和正态分布，方差分析结果如下：
med_ls = [&#39;medicine_a&#39;,&#39;medicine_a&#39;,&#39;medicine_a&#39;,&#39;medicine_a&#39;,&#39;medicine_a&#39;,&#39;medicine_a&#39;,&#39;medicine_a&#39;,&#39;medicine_a&#39;
      ,&#39;medicine_b&#39;,&#39;medicine_b&#39;,&#39;medicine_b&#39;,&#39;medicine_b&#39;,&#39;medicine_c&#39;,&#39;medicine_c&#39;,&#39;medicine_c&#39;,&#39;medicine_c&#39;,
      &#39;medicine_c&#39;,&#39;medicine_c&#39;,&#39;medicine_c&#39;,&#39;medicine_d&#39;,&#39;medicine_d&#39;,&#39;medicine_d&#39;,&#39;medicine_d&#39;,&#39;medicine_d&#39;,
      &#39;medicine_d&#39;]
recov_ls = [80,203,236,252,284,368,457,393,133,180,100,160,156,295,320,448,465,481,885,194,214,272,330,386,475]
df = pd.DataFrame([med_ls,recov_ls],index=[&#39;med&#39;,&#39;nums&#39;]).T
data_new = df.dropna()
data_new[&#39;nums&#39;] = data_new[&#39;nums&#39;].apply(pd.to_numeric)
model = ols(&#39;nums ~ C(med)&#39;,data_new).fit()
table = no.anova_lm(model)
print(table)

图6

图6就是对应方差分析的结果。
七：非参数检验之K-S分布检验

Kolmogorov-Smirnov(K-S)分布检验是一种非常重要的非参数检验方法。它是一种统计检验方法，它通过比较两样本的频率分布，或者一个样本的频率分布与特定理论分布（如正态分布、泊松分布等）之间的差异大小来推论两个分布是否来自同一个分布。
KS检验的原假设 $H_0:$ 对所有 $x$ 的值， $F(x)=F_0(x)$ ，那么双尾的备择假设为 $H_1:$ 对至少一个 $x$ 值， $F(x)\ne F_0(x)$ 。我们令 $S(x)$ 表示该组数据的经验分布，一般来说随机样本 $X_1,X_2,...X_n$ 的经验分布函数定义为阶梯函数：
$S(x)=\frac{X_i\leq x的个数}{n}$ ，它是小于等于 $x$ 值的比例，它是总体分布 $F(x)$ 的一个估计，对于双尾检验，检验统计量设为： $D=sup_x\left| S(X)-F_0(X) \right|$ 。

注：统计量 $D$ 的分布实际上在零假设下对于一切连续分布 $F_0(x)$ 是一样的，所以与分布无关。由于 $S(x)$ 是阶梯函数，只取离散值，考虑到跳跃问题，在实际运作中，如果有 $n$ 个观测值，则下面的统计量来代替 $D$ ， $D_n=max(i\in[1,n])\left\{ max\left( \left| S(x_i)-F_0(x_i) \right|,\left| S(x_{i-1})-F(x_i) \right| \right) \right\}$ 。

关于qq图检验的运用

qq图检验数据分布是一种非常直观的方法了。由于样本 $x$ 的分位数为其经验累积分布函数的逆函数，如果把数据列 $x$ 的经验分位数点对一个已知分布的相应分位数点画出散点图，那么当 $x$ 的经验分布类似于已知分布时，图形就近似地形成一条斜率为1的直线，否则，图形中端部就会较大地偏离这个直线。
我们用Python感受这一过程：
import matplotlib.pyplot as plt
from scipy import stats
norm_arr = np.random.uniform(0,1,10000)
stats.probplot(norm_arr, dist=&#39;uniform&#39;, plot=plt)
plt.show()
stats.probplot(norm_arr, dist=&#39;norm&#39;, plot=plt)
plt.show()

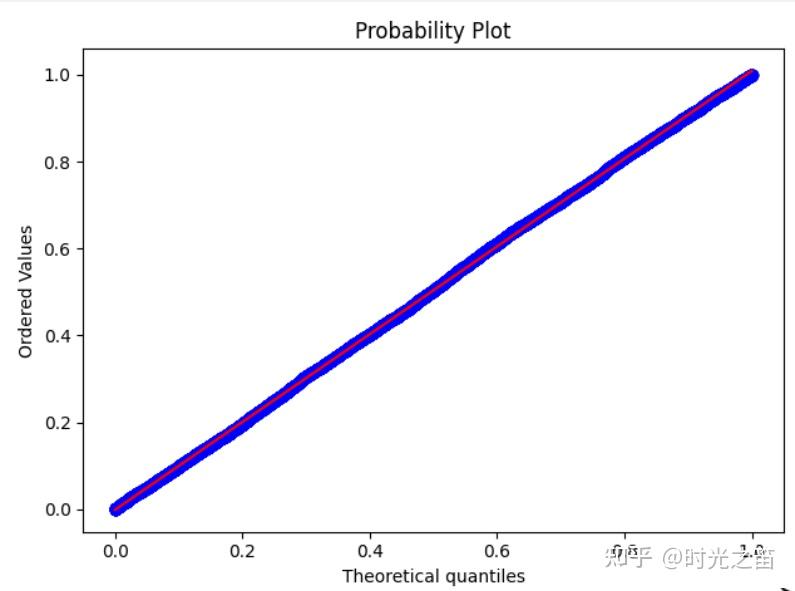
图7

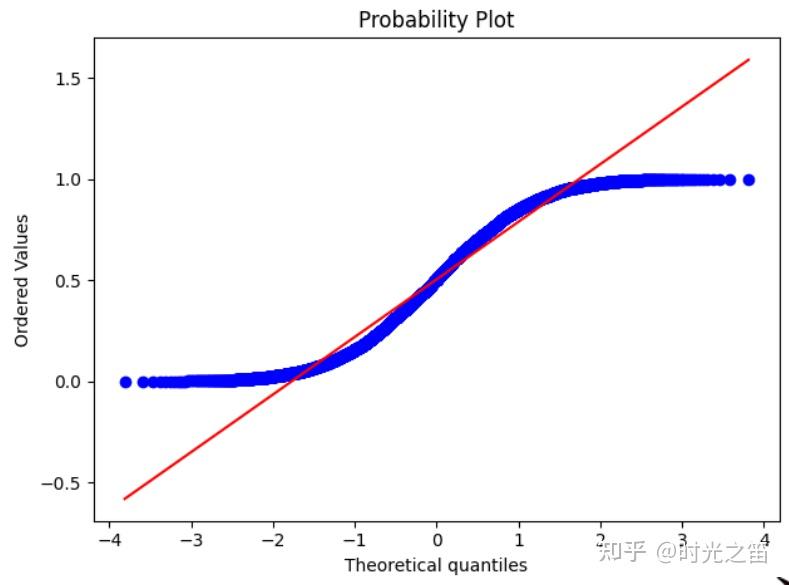
图8

我们已知给定的数据是上下限为0-1的均匀随机数，图7是dist=&#39;uniform&#39;时的结果，图8是dist=&#39;norm&#39;时的结果，明显直观感觉到qq图方法的直观性，且原本随机数是服从均匀分布的！
关于KS检验的运用

我们对上述数据用KS检验法看看结果如何：
res = stats.kstest(norm_arr,&#39;uniform&#39;,alternative=&#39;two-sided&#39;)
print(&#39;\033[1;33m用KS检验方法检验上述随机数分布：\033[0m&#39;,res)

图9

从 $p$ 值结果看，很明显原本随机数是服从均匀分布的，接受原假设。
接着我们对两组或两组以上数据运用KS检验方法观察结果：
arr1 = np.random.uniform(0,1,100)
arr2 = np.random.normal(0,1,100)
res1 = stats.ks_2samp(arr1,arr2)
print(&#39;\033[1;31m一个正态分布N~(0,1)，一个均匀分布U~(0,1)的检测结果：\033[1;0m&#39;,res1)

arr1 = np.random.normal(0,1,100)##数据长度不一致也可行！！
arr2 = np.random.normal(0,1,150)
res2 = stats.ks_2samp(arr1,arr2)
print(&#39;\033[1;32m两个都是正态分布N~(0,1)的检测结果：\033[1;0m&#39;,res2)

注：如果是检验非标准正态分布，则stats.kstest(norm_arr,&#39;norm&#39;,(mean,std),alternative=&#39;two-sided&#39;)即可！

综上，我们能感受到KS检验的方便性和适用性，但对于是否服从正态分布等检验的检验方法不止局限上述两种，还有Shapiro-Wilk正态检验、历史悠久的 $\chi^2$ 检验等等。
八：总结

本篇文章主要是关于统计学中常见和重要的检验分析。其它参数检验如 $F$ 检验，非参数检验如二项检验、游程检验等等，都是类似的原理和方法。熟练运用以上6种检验能解决生活和生产中很多问题了，学习其它方法（比如金融方面的平稳性检验、格兰杰检验等等，随机过程方面的随机性检验、白噪声等等）也会更加游刃有余。
但我们一定要清楚统计检验和统计分布的概念区别，检验是对样本统计量进行一系列操作，分布则就是指一些数据（一般指随机变量）符合何种概率或者概率密度分布。所以卡方检验和卡方分布是完全不同的两个概念！

感恩由您 · 发表于 2024-12-26 12:13

你说的这几种检验方法，都是对单个正态总体参数的假设检验。
（1）首先解释为什么正态总体假设检验比较常见，正态分布比较常见，一般假定现象都服从正态分布，当然也可以对数据做正态性检验；
（2）其次什么是正态分布？正态分布有两个参数，第一个参数是正态分布的均值，第二次参数是正态分布的方差，均值在统计学上表示现象的一般水平，方差代表离散程度，所以说对单个正态总体参数的假设检验，也就是对正态分布均值，方差的检验；
（3）t检验，总体方差已知的情况下，对正态总体均值的检验，通俗点说，就是在正态总体第二个参数已知的条件下，样本的均值应该和总体的均值相差不大，总体均值使我们希望的了解的，比如说包装奶粉，标准是每桶500g，由于在生产过程中机器的损耗、加工的环境等因素的影响，可能会偏离这个标准，那么怎么了解这个总体的平均值是不是为500g呢？当然是通过抽样，因为我不能调查全部生产的奶粉的重量，随机抽取一定数量的奶粉，比如说10桶，来称取这10桶奶粉的重量，一个很自然的想法就是如果总体的均值是500，那么这10桶奶粉的均值也应该和500相差不大，由于随机性的影响，在统计中允许有一定的误差，但是要确定这个误差的数值，也就是说我允许抽样的均值大于或小于500，但是得给定一个范围，于是就有了t检验；
（4）U检验，总体方差未知的情况下，对正态总体均值的检验，通俗点说，同上；
（5）卡方检验，对总体方差的检验，也就是对正态总体第二个参数的检验，理解t检验后，道理是一样的，只不过换了条件，换了检验的参数。
至于为什么不同的参数，不同的条件检验方法不同，可以查看三大抽样分布。

图文播报

[分享] 如何形象地理解统计学中的各种检验方法？

登陆有奖并可浏览互动！

发表回复

官方推荐 /3

个人中心