深入解析Flow Matching技术

青草

【随着Stable Diffusion 3的发布，Flow Matching技术逐渐进入公众视野，成为了学术界和工业界关注的焦点。本文将梳理并阐述Flow Matching的核心概念，详细解读其在生成模型中的应用，并探讨其背后的数学原理。】



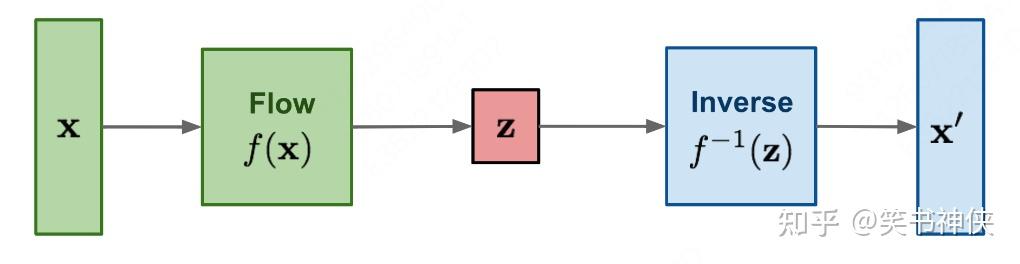
Fig.1 Illustration of a Flow-based model

Flow-based Model是一种基于Normalizing Flows(NFs)的生成模型，它通过一系列概率密度函数的变量变换，将复杂的概率分布转换为简单的概率分布，并通过逆变换生成新的数据样本。而Continuous Normalizing Flows(CNFs)是Normalizing Flows的扩展，它使用常微分方程(ODE)来表示连续的变换过程，用于建模概率分布。
Flow Matching(FM)是一种训练Continuous Normalizing Flows的方法，它通过学习与概率路径相关的向量场(Vector Field)来训练模型，并使用ODE求解器来生成新样本。
扩散模型是Flow Matching的一个应用特例，使用FM可以提高其训练的稳定性。此外,使用最优传输(Optimal Transport)技术构建概率路径可以进一步加快训练速度，并提高模型的泛化能力。

<hr/>一、概率密度函数的变量变换

给定一个随机变量 z 及其概率密度函数 z\sim\pi(z) ，通过一个一对一的映射函数 f 构造一个新的随机变量 x=f(z) 。如果存在逆函数 f^{-1} ，那么新变量 x 的概率密度函数 p(x) 计算如下：
（1）当\bold{z}为随机变量：
p(x)=\pi(z)\left|\frac{d z}{d x}\right|=\pi\left(f^{-1}(x)\right)\left|\frac{d f^{-1}}{d x}\right|=\pi\left(f^{-1}(x)\right)\left|\left(f^{-1}\right)^{\prime}(x)\right|
（2）当\bold{z} 为随机向量：
p(\mathbf{x})=\pi(\mathbf{z})\left|\operatorname{det} \frac{d \mathbf{z}}{d \mathbf{x}}\right|=\pi\left(f^{-1}(\mathbf{x})\right)\left|\operatorname{det} \frac{d f^{-1}}{d \mathbf{x}}\right|
其中，det是行列式， \frac{d \mathbf{f}}{d\mathbf{x}} 是雅可比矩阵。
特例：如果 x \sim N\left(\mu, \sigma^{2}\right) ，当a,b为实数时，则有 z = f(x) = a x+b \sim N\left(a \mu+b,(a \sigma)^{2}\right)
二 、Normalizing Flows

Normalizing Flows(NFs)是一种可逆的概率密度变换方法，它的核心思想是通过一系列可逆的变换函数来逐步将一个简单分布（通常是高斯分布）转换成一个复杂的目标分布。这个过程可以被看作是一连串的变量替换的迭代过程，每次替换都遵循概率密度函数的变量变换原则。通过这种方式，Normalizing Flows能够精确地计算出变换后的分布的概率密度，从而实现从简单分布到复杂分布的精确映射。



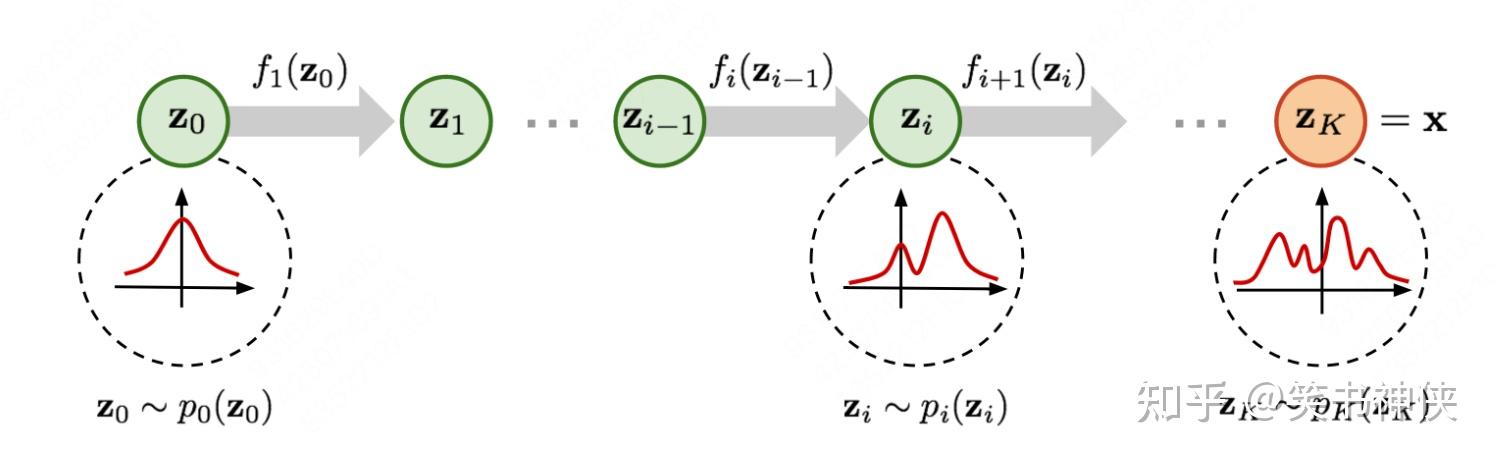
Fig.2 Illustration of a normalizing flow model

设 p_{0}\left(\mathbf{z}_{0}\right) 是原始的简单分布（例如标准高斯分布），Normalizing Flows希望通过一系列可逆变换 \left\{ f_i \right\} 将其转换成目标分布 p(x) 。这些变换定义了从 z_0 到 x 的映射，并且每一步变换 f_i ​都有其逆变换 f_{i}^{-1} 。那么，变换过程可以表示为：
\mathbf{x}=\mathbf{z}_{K}=f_{K} \circ f_{K-1} \circ \cdots \circ f_{1}\left(\mathbf{z}_{0}\right)
对于其中第 i 步，有：
\begin{array}{l} \mathbf{z}_{i-1} \sim p_{i-1}\left(\mathbf{z}_{i-1}\right) \\ \mathbf{z}_{i}=f_{i}\left(\mathbf{z}_{i-1}\right), \text { thus } \mathbf{z}_{i-1}=f_{i}^{-1}\left(\mathbf{z}_{i}\right) \end{array}
根据率密度函数的变量变换关系可得：
\begin{aligned} p_{i}\left(\mathbf{z}_{i}\right) & =p_{i-1}\left(f_{i}^{-1}\left(\mathbf{z}_{i}\right)\right)\left|\operatorname{det} \frac{d f_{i}^{-1}}{d \mathbf{z}_{i}}\right| \\ & =p_{i-1}\left(\mathbf{z}_{i-1}\right)\left|\operatorname{det}\left(\frac{d f_{i}}{d \mathbf{z}_{i-1}}\right)^{-1}\right| \\ & =p_{i-1}\left(\mathbf{z}_{i-1}\right)\left|\operatorname{det} \frac{d f_{i}}{d \mathbf{z}_{i-1}}\right|^{-1} \end{aligned}
其对数似然为：
\log p_{i}\left(\mathbf{z}_{i}\right)=\log p_{i-1}\left(\mathbf{z}_{i-1}\right)-\log \left|\operatorname{det} \frac{d f_{i}}{d \mathbf{z}_{i-1}}\right|
给定这样一连串的概率密度函数和变换关系，可以逐步展开直至追溯到初始分布，可得：
\begin{aligned} \log p(\mathbf{x})=\log \pi_{K}\left(\mathbf{z}_{K}\right) & =\log \pi_{K-1}\left(\mathbf{z}_{K-1}\right)-\log \left|\operatorname{det} \frac{d f_{K}}{d \mathbf{z}_{K-1}}\right| \\ & =\log \pi_{K-2}\left(\mathbf{z}_{K-2}\right)-\log \left|\operatorname{det} \frac{d f_{K-1}}{d \mathbf{z}_{K-2}}\right|-\log \left|\operatorname{det} \frac{d f_{K}}{d \mathbf{z}_{K-1}}\right| \\ & =\ldots \\ & =\log \pi_{0}\left(\mathbf{z}_{0}\right)-\sum_{i=1}^{K} \log \left|\operatorname{det} \frac{d f_{i}}{d \mathbf{z}_{i-1}}\right| \end{aligned}
当这一系列变换函数 f_i 可逆，且雅可比矩阵易于计算，模型训练时，优化目标为负对数似然：
\mathcal{L}(\mathcal{D})=-\frac{1}{|\mathcal{D}|} \sum_{\mathbf{x} \in \mathcal{D}} \log p(\mathbf{x})
三、Continuous Normalizing Flows

Continuous Normalizing Flows (CNFs) 是 Normalizing Flows 的一种扩展，它可以更好地建模复杂的概率分布。在传统的Normalizing Flows中，变换通常是通过一系列可逆的离散函数来定义的，而在CNFs中，这种变换是连续的，这使得模型能够更加平滑地适应数据的分布，提高了模型的表达能力。CNFs过程通过常微分方程（ODE）来表示：
{\color{Red} {\frac{d z_t}{d t}=v(z_t, t)} }
其中， t \in [0,1] ，z_t 是Flow Map，或者Transport Map，可简单理解为时间 t 下的数据点， v(z_t,t) 是一个向量场，它定义了每一个数据点在状态空间中随时间的变化方向和大小，通常为神经网络预测。
如果知道了这个向量场v(z_t,t) ，那么通过求解这个 ODE就可以找到从初始概率分布到目标概率分布的连续路径，从而将简单分布转换成复杂分布。这个ODE可以采用欧拉方法来求解，从初始值 z_0  开始，使用下面的迭代公式来计算 z 在后续时间点的近似值：
z_{t+\Delta t}=z_{t}+\Delta t \cdot v\left(z_{t}, t\right)
其中， \Delta t = 1/N 是步长， t=i/N是采样时间点， N 是最大采样步数，z_t 是在时间   t 的近似解。
这意味着，给定一个初始概率分布（通常是标准高斯分布），向量场 v(z_t,t) 可以描述这个分布随时间的演变，最终达到目标分布。这是CNFs建模复杂概率分布的基础，即可以通过学习向量场来学习数据的变换过程。
四、Continuity Equation

在物理学里，Continuity Equation是描述守恒量传输行为的偏微分方程。在适当条件下，质量、能量、动量、电荷等都是守恒量，因此很多传输行为都可以用连续性方程来描述。



Fig.3 Illustration of vector field

连续性方程的一般形式是通过对流体的质量守恒定律进行数学推导得到的：
\frac{\partial \rho}{\partial t}+ \mathrm{div} ( \rho \mathbf{v})=0

• \rho 是流体的密度。
  
• \mathbf{v}  是流体的速度矢量。
  
• \frac{\partial \rho}{\partial t} 是密度随时间的变化率。
  
• \operatorname{div}(\rho \mathbf{v}) 是质量通量密度的散度，表示单位时间内通过单位面积的净质量流量。
  

这个方程表明，流体密度的时间变化率加上质量通量密度的散度等于零。换句话说，流体中任何封闭体积内的质量变化率等于流入和流出该体积的质量流量的差。
由于概率密度函数的性质确保了在全体分布上的积分为1，这反映了概率的总和是固定的，即概率是守恒的。在CNFs中，可以将这个性质与流体力学中的连续性方程类比，从而得到概率密度的连续性方程：
{\color{Red} {\frac{\partial p_{t}(x)}{\partial t}+\mathbf{div} \left(p_{t}(x) \mathbf{v}_{t}(x)\right)=0}}  ⭐️
其中， p_t(x) 是 t 时刻的概率密度函数， v_t(x) 是与p_t(x)相关联的向量场，它描述了概率密度随位置和时间的变化， \operatorname{div}\left(p_{t}(x) \mathbf{v}_{t}(x)\right) 是向量场与概率密度的乘积的散度，表示概率流通过某个区域的净变化率。
性质：Continuity Equation是判断向量场v_t(x) 产生对应的概率密度路径 p_t(x)的充分必要条件。如果向量场v_t(x) 和概率密度路径 p_t(x) 满足Continuity Equation，则在CNFs中该向量场v_t(x) 就能产生对应的概率密度路径 p_t(x) 。
五、 Conditional and Marginal Probability Paths and  Vector Fields

对于目标分布为 q(x_1)的每个数据样本 x_1，可以定义一个随时间变化的条件概率路径  p_t(x|x_1) 。对条件概率路径进行边缘化积分，就得到了一个边缘概率路径：
p_{t}(x)=\int p_{t}\left(x \mid x_{1}\right) q\left(x_{1}\right) d x_{1}
这个边缘概率路径考虑了所有样本及其对应的条件概率路径。
通过对条件向量场进行加权并边缘积分到边缘向量场：
\mathbf{{\color{Green}{ u_{t}(x)=\int u_{t}\left(x \mid x_{1}\right) \frac{{\color{Red}{ p_{t}(x \mid x_{1})}}  q(x_{1}) }{\color{Red} {p_{t}(x)}}  d x_{1}}} }  ⭐
在数据点 x 处的向量场 u_t(x) 是通过对所有可能的初始条件 x_1 的条件向量场 u_{t}\left(x \mid x_{1}\right) 加权积分得到的，权重是由条件概率密度 p_{t}\left(x \mid x_{1}\right) 和边缘概率密度 p_t(x) 的比值决定的。
这个公式十分重要，是连接条件向量场和边缘向量场的桥梁。论文通过Theorem 1进行了总结，只要条件向量场 u_t(x|x_1) 能生成对应的条件概率路径 p_t(x|x_1)（满足连续性条件），那么上述边缘向量场 u_t(x) 能够生成对应的边缘概率路径 p_t(x)。
Theorem 1: 给定向量场 u_t(x|x_1) ，它生成条件概率路径 p_t(x|x_1) ，对于任何分布 q(x_1) ，上述定义的边缘向量场 u_t(x) 就能生成对应的边缘概率路径 p_t(x)。
六、Flow Matching

训练Continuous Normalizing Flows的直观方法是，在给定初始条件 x_0 ​的情况下，通过ODE求解得到的 x_1 ​的分布，然后通过一种最小化差异度量（如KL散度）来约束 x_1 与真实数据的分布保持一致。然而，由于中间轨迹多而且未知，推断 x_1（通过采样或者计算似然概率） 需要反复模拟ODE，计算量非常巨大。为此，论文提出了新的方法Flow Matching（FM）。
Flow Matching是一种适用于训练Continuous Normalizing Flows的技术，它是Simulation-Free的，即无需通过ODE推理目标数据分布。它的核心思想在于，通过确保模型预测的向量场与描述数据点实际运动的向量场之间的动态特性保持一致性，从而确保通过CNFs变换得到的最终概率分布与期望的目标分布相匹配。
具体来说，给定一个目标概率密度路径  p_t(x) 及其对应的向量场 u_t(x) ，这里的概率密度路径  p_t(x) 是由这个向量场 u_t(x) 生成的， v_t(x) 是待学习的向量场，那么Flow Matching的优化目标可以定义为：
{\color{Red} {\mathcal{L}_{\mathrm{FM}}(\theta)=\mathbb{E}_{t, p_{t}(x)}\left\|v_{t}(x)-u_{t}(x)\right\|^{2}} } ⭐️
其中， t \sim U[0, 1]， x \sim p_t(x)  ，保证在整个时间范围和数据范围内对模型进行训练，确保模型能够处理从初始分布到目标分布的整个转换过程。Flow Matching 目标的核心是最小化这个损失函数，使得它预测的向量场 v_t(x)  尽可能接近于实际的向量场 u_t(x) ，从而能够准确地生成目标概率密度路径  p_t(x) 。
Flow Matching 看起来很直观，但由于缺乏先验知识来确定合适的 p_t(x) 和 u_t(x) ，因此无法直接使用。因为尽管存在许多概率路径使得变换后的概率分布与目标分布相同或接近，但通常无法得到一个的封闭形式的向量场u_t(x)来生成期望的概率路径的 p_t(x)。
为了解决这个问题，论文提出Conditional Flow Matching，可以采用一种基于样本的方法，为每个样本独立地定义概率路径和向量场，而不是依赖于一个全局的、封闭形式的向量场，然后通过适当的聚合方法，将这些个体样本的概率路径和向量场聚合起来以生成所需的p_t(x) 和 u_t(x)。
七、 Conditional Flow Matching

由于 u_t(x) 难以直接获得，也难以通过u_t(x|x_1)进行边缘积分计算得到，因此直接优化原始Flow Matching目标函数不可行。
论文提出了Conditional Flow Matching方法，只要u_t(x|x_1)和u_t(x)满足上述加权边缘积分条件，那么Conditional Flow Matching优化目标与原始Flow Matching目标函数具有相同的最优解。Conditional Flow Matching优化目标为：
{\color{Red} {\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t, q\left(x_{1}\right), p_{t}\left(x \mid x_{1}\right)}\left\|v_{t}(x)-u_{t}\left(x \mid x_{1}\right)\right\|^{2}} }
论文通过Theorem2进行了证明了Conditional Flow Matching优化目标与原始Flow Matching目标函数具有相同梯度，也即具有相同的最优解。
Theorem 2: 假设对于所有的 x \in \mathbb{R}^{d} 和 t \in [0,1] ，都有 p_{t}(x)>0 ，那么 \mathcal{L}_{\mathrm{CFM}} 和 \mathcal{L}_{\mathrm{FM}} 相差一个与 \theta 无关的常数，即有 \nabla_{\theta} \mathcal{L}_{F M}(\theta)=\nabla_{\theta} \mathcal{L}_{C F M}(\theta) 。
性质：优化Conditional Flow Matching目标等同于优化Flow Matching目标，从而无需计算边缘概率路径或边缘向量场，只需要设计一个合适的条件概率路径和向量场即可。
八、Calculate Conditional Probability Paths and Conditional Vector Fields

Conditional Flow Matching可以选择任意的条件概率路径，只要满足边界条件即可，这里针对一般高斯条件概率路径，分析如何构建 p_{t}\left(x \mid x_{1}\right) 和 u_{t}\left(x \mid x_{1}\right) 。
假设条件概率路径为高斯概率路径：
{\color{Green}{ p_{t}\left(x \mid x_{1}\right)=\mathcal{N}\left(x \mid \mu_{t}\left(x_{1}\right), \sigma_{t}\left(x_{1}\right)^{2} I\right)}}  
只要满足如下两个边界条件，就能作为条件概率路径：

• 在时间开始时  (t = 0) ，满足 \mu_{0}\left(x_{1}\right) \text = 0 , \sigma_{0}\left(x_{1}\right) = 1 ，确保所有的条件概率路径都会收敛到相同的标准高斯噪声分布，即 p(x)=\mathcal{N}(x \mid 0, I) 。
  
• 在时间进行到 (t = 1)，满足 \mu_{1}\left(x_{1}\right) \text = x_1 , \sigma_{1}\left(x_{1}\right) = \sigma_{min} ，这个 \sigma_{min} 值要设定得足够小，确保 p_{1}\left(x \mid x_{1}\right) 是一个均值为 x_1 、方差很小的高斯分布，这样条件概率路径会收敛到 x_1 附近。
  

这种设定方式定义了一个确定的变换过程，从 t=0 时的标准高斯分布开始，逐渐转变为 t=1 时的目标分布。
对于一个概率路径，存在无限多个向量场可以生成它，比如通过向Continuity Equation添加一个无散度分量，但这会导致不必要的计算量，这里可以使用最简单的向量场，它对应于高斯分布的标准变换，对应的数据点Flow Map为：
{\color{Green} {\mathbf{\psi_{t}(x)=\sigma_{t}\left(x_{1}\right) x+\mu_{t}\left(x_{1}\right)} }}  
可以根据概率密度变量变换可以直接得出，这个Flow Map满足上述高斯概率路径。
根据第三节中CNFs关于向量场的定义，求解以下ODE，可以得到对应的条件向量场u_{t}\left(x \mid x_{1}\right)：
\frac{d}{d t} \psi_{t}(x)=u_{t}\left(\psi_{t}(x) \mid x_{1}\right)  
注意，该ODE中 u_t 是关于 \psi_t(x) 的函数。
论文通过Theorem 3进行推导得到了条件向量场的封闭解。
Theorem 3：设p_{t}\left(x \mid x_{1}\right) 为上述高斯概率路径， \psi_t(x) 为其对应的Flow Map，那么 \psi_t(x) 具有的唯一向量场 u_{t}\left(x \mid x_{1}\right) ，其形式为：
\mathbf{{\color{Green} {u_{t}\left(x \mid x_{1}\right)=\frac{\sigma_{t}^{\prime}\left(x_{1}\right)}{\sigma_{t}\left(x_{1}\right)}\left(x-\mu_{t}\left(x_{1}\right)\right)+\mu_{t}^{\prime}\left(x_{1}\right)}} }  
该向量场u_{t}\left(x \mid x_{1}\right)  可以生成对应的高斯概率路径 p_{t}\left(x \mid x_{1}\right) 。
性质：得到了 u_{t}\left(x \mid x_{1}\right) 就可以根据Conditional Flow Matching的优化目标 \mathcal{L}_{\text {CFM }} 进行优化，从而得到待学习的全局向量场 v_t(x) ，优化过程的关键就在于找到合适的条件向量场 u_{t}\left(x \mid x_{1}\right) 。
值得注意的是，这里选择高斯概率密度路径只是可选方式之一，实际上可以根据需要设计任何合理的路径，SD3也是Conditional Flow Match的一种应用。
九、Diffusion conditional Vector Fields and Optimal Transport  conditional Vector Fields

Flow Map公式设计时，允许使用各种可微分函数来定义  \mu_t(x_1)  和 \( \sigma_t(x_1) \) ，所以可以根据不同的应用场景和边界条件选择合适的函数。下面介绍两种特例，Diffusion conditional Vector Fields 和 Optimal Transport  conditional Vector Fields 。



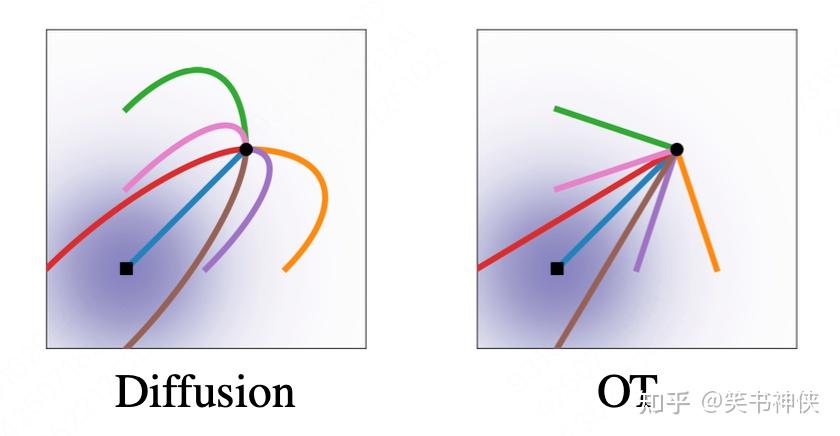
Fig.4 Diffusion and OT trajectories

9.1  Diffusion conditional Vector Fields

扩散模型中的Variance Exploding (VE)和Variance Preserving (VP)是两种不同类型的扩散过程，它们在生成模型中用于模拟两种不同的数据分布变化过程。
（1）Variance Exploding (VE): VE扩散模型是一种在生成过程中增加数据方差的扩散过程。在这种模型中，随着时间的推移，数据样本会逐渐变得更加嘈杂，即方差会不断增大，直到达到一个稳定的状态。VE过程的一个特点是，它允许模型在生成数据时探索更广泛的潜在空间，这有助于生成多样化的样本。
VE的条件概率路径为：
p_{t}\left(x \mid x_{1}\right)=\mathcal{N}\left(x \mid x_{1}, \sigma_{1-t}^{2} I\right)
其中， \sigma_t 是递增函数， \sigma_0=0, \sigma_1\gg1 ，对应均值和标准差 \mu_{t}\left(x_{1}\right)=x_{1} \text { , } \sigma_{t}\left(x_{1}\right)=\sigma_{1-t} 。
根据Theorem 3可以计算条件向量场为：
u_{t}\left(x \mid x_{1}\right)=-\frac{\sigma_{1-t}^{\prime}}{\sigma_{1-t}}\left(x-x_{1}\right)
（2）Variance Preserving (VP): VP扩散模型是一种在生成过程中保持数据方差不变的扩散过程。在这种模型中，数据样本在生成过程中的方差保持恒定，这意味着模型在引入噪声的同时，也会以某种方式减少噪声，以保持数据的整体方差不变。VP模型通常用于那些需要保持数据分布稳定性的应用场景，例如在图像生成中保持图像的清晰度和结构特征。
VP的条件概率路径为：
p_{t}\left(x \mid x_{1}\right)=\mathcal{N}\left(x \mid \alpha_{1-t} x_{1},\left(1-\alpha_{1-t}^{2}\right) I\right), \text { where } \alpha_{t}=e^{-\frac{1}{2} T(t)}, T(t)=\int_{0}^{t} \beta(s) d s
其中， \alpha,\beta 为噪声策略函数，对应均值和标准差 \mu_{t}\left(x_{1}\right)=\alpha_{1-t} x_{1},\sigma_{t}\left(x_{1}\right)=\sqrt{1-\alpha_{1-t}^{2}} 。
根据Theorem 3可以计算条件向量场为：
u_{t}\left(x \mid x_{1}\right)=\frac{\alpha_{1-t}^{\prime}}{1-\alpha_{1-t}^{2}}\left(\alpha_{1-t} x-x_{1}\right)=-\frac{T^{\prime}(1-t)}{2}\left[\frac{e^{-T(1-t)} x-e^{-\frac{1}{2} T(1-t)} x_{1}}{1-e^{-T(1-t)}}\right]
结论：实验发现，将扩散模型条件向量场与Flow Matching目标结合起来优化，相比于现有的Score Matching方法，训练更加稳定。
9.2 Optimal Transport  conditional Vector Fields

最优传输(Optimal Transport，简称OT)选择定义条件概率路径的均值和标准差为简单的时间线性函数，当时间 t:0\rightarrow1 ，对应概率密度路径从p(x)=\mathcal{N}(x \mid 0, I)到 p_{1}\left(x \mid x_{1}\right) ，均值和标准差定义为：
\mu_{t}(x)=t x_{1}, \text { and } \sigma_{t}(x)=1-\left(1-\sigma_{\min }\right) t
那么可得其对应Flow Map为：
\psi_{t}(x)=\left(1-\left(1-\sigma_{\min }\right) t\right) x+t x_{1}
根据Theorem 3可计算条件向量场的封闭解为：
u_{t}\left(x \mid x_{1}\right)=\frac{x_{1}-\left(1-\sigma_{\min }\right) x}{1-\left(1-\sigma_{\min }\right) t}
结论：最优传输路径轨迹为直线，而扩散路径轨迹为曲线，因而可以得到更快的训练速度和生成速度，以及更好的性能表现。
十、参考文献

• Flow Matching for Generative Modeling
  
• Continuity equation
  
• Flow-based Deep Generative Models
  

<hr/>【END】

原文地址：https://zhuanlan.zhihu.com/p/685921518