登陆有奖并可浏览互动!
您需要 登录 才可以下载或查看,没有账号?立即注册


×
对于反演: \textbf{Gm=d}\\直接求解矩阵G的逆,得到待求参数,不行吗?\textbf{m}=\textbf{G}^{-1}\textbf{b}\\还真不行,不要忘了,只有方阵,即行数等于列数的矩阵才能求逆。我们如何保证矩阵G为方阵呢?也就是,如何保证待求参数个数等于观测数据的数量呢?
那你要说,这好办,方程两边同乘矩阵G的转置: \textbf{G}^{T}\textbf{Gm}=\textbf{G}^{T}\textbf{d}\\ \textbf{G}^{T}\textbf{G} 就是方阵了,那就可以求逆了吧: m=(\textbf{G}^{T}\textbf{G})^{-1}\textbf{G}^{T}\textbf{d}\\ 这样看上去可以,但实际情况是:由于观测非常有限,(1) \textbf{G}^{T}\textbf{G} 的条件数往往非常大,也就是最大特征值与最小特征值的比值非常大,(2)甚至存在特征值为0的情况(秩亏)。
那么,对于(1)条件数很大的情况,直接求逆非常不稳定,因此难以得到想要的结果。(2)对于有特征值为0的情况,根本无法求逆。那咋办?
加约束呗,反演不稳定,加约束;反演无解,加约束。总之就是遇到问题,想想如何加约束。
约束包括:先验信息+正则化操作。常见的约束方法有:在矩阵 \textbf{G}^{T}\textbf{G} 后面加上一个单位阵*系数: \textbf{G}^{T}\textbf{G}+\varepsilon^2\textbf{I} ,这样能改善其条件数过大的问题。
下面仔细讲讲:先验信息都是高斯分布,且正演公式是线性的,如何求解此线性反演问题。
1 公式推导
假设观测数据与模型参数都符合高斯分布,本小节目的是推导出具体公式,即最小二乘解。
(1) 观测数据为高斯分布: \rho_{D}(\textbf{d})=\rm const. exp(-\frac{1}{2}(\textbf{d}-\textbf{d}_{obs})^t \textbf{C}_{d}^{-1}(\textbf{d}-\textbf{d}_{obs}))\\ \textbf{C}_{d} 为协方差矩阵,表示观测数据的不确定性;
(2) 正演计算d=Gm,不确定性也是高斯分布的: \theta(\textbf{d}|\textbf{m})=\rm const. exp(-\frac{1}{2}(\textbf{d}-\textbf{Gm})^t \textbf{C}_{T}^{-1}(\textbf{d}-\textbf{Gm})\\ \textbf{C}_{T} 代表正演理论的不确定性。
对于上面两个式子,在计算模型参数的后验分布时,需要计算似然函数: L=\rm const.\int_{}^{}\rho_{D}(\textbf{d})\theta(\textbf{d}|\textbf{m}) d \textbf{d}\\ 由两个高斯分布卷积仍是高斯分布,可知: L(\textbf{m})=\rm const. exp(-\frac{1}{2}(\textbf{Gm}-\textbf{d}_{obs})^t \textbf{C}_{D}^{-1}(\textbf{Gm}-\textbf{d}_{obs})\\ 其中, \textbf{C}_{D}=\textbf{C}_{T}+\textbf{C}_{d} 。
这意味着利用高斯分布的性质,非常巧妙地把观测数据与正演算子的不确定性合二为一。
该性质证明见:Tarantola反演书的202页6.21节。
(3)模型空间参数分布也是高斯的: \rho_{M}(\textbf{m})=\rm const. exp(-\frac{1}{2}(\textbf{m}-\textbf{m}_{prior})^t \textbf{C}_{M}^{-1}(\textbf{m}-\textbf{m}_{prior}))\\ 由后验概率分布公式: \sigma_{M}(\textbf{m})=\rm const.\rho_{M}(\textbf{m})L(\textbf{m})\\ 可知: \sigma_{M}(\textbf{m})=\rm const.exp(-S(\textbf{m}))\\ 其中, \textbf{S(m)}=\frac{1}{2}[(\textbf{Gm}-\textbf{d}_{obs})^t \textbf{C}_{D}^{-1}(\textbf{Gm}-\textbf{d}_{obs})+(\textbf{m}-\textbf{m}_{prior})^t \textbf{C}_{M}^{-1}(\textbf{m}-\textbf{m}_{prior})]\\ 现在目的是让后验概率 \sigma_{M}(\textbf{m}) 最大,则 \textbf{S(m)} 应该最小,也就是求其最小值。
由于S(m)是关于m的二次函数,令在其中心估计值\tilde{\textbf{m}} 处, \textbf{S(m)} 值最小,则在 \tilde{\textbf{m}} 处, \textbf{S(m)} 的一阶导数应为0: \frac{\partial \textbf{S}}{\partial \textbf{m}}|_{\textbf{m}=\tilde{\textbf{m}}}=0\\ 由矩阵求导公式(https://www.math.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf): \frac{\partial }{\partial X}(Xb+C)^tD(Xb+C)= (D + D^t )(Xb + c)b^t\\ 由 \textbf{S(m)} 定义式可知其一阶导数为(注意协方差矩阵为对角阵): \frac{\partial \textbf{S}}{\partial \textbf{m}}=\textbf{G}^{t}\textbf{C}_{D}^{-1}(\textbf{Gm}-\textbf{d}_{obs})+\textbf{C}_{M}^{-1}(\textbf{m}-\textbf{m}_{prior})\\ 把 \textbf{m}=\tilde{\textbf{m}} 带入上式,由一阶导数为0可得: (\textbf{G}^{t}\textbf{C}_{D}^{-1}\textbf{G}+\textbf{C}_{M}^{-1})\tilde{\textbf{m}}=\textbf{G}^t\textbf{C}_{D}^{-1}\textbf{d}_{obs}+\textbf{C}_{M}^{-1} \textbf{m}_{prior}\\ 那么待求参数 \tilde{\textbf{m}} 为: \tilde{\textbf{m}}=(\textbf{G}^{t}\textbf{C}_{D}^{-1}\textbf{G}+\textbf{C}_{M}^{-1})^{-1}(\textbf{G}^t\textbf{C}_{D}^{-1}\textbf{d}_{obs}+\textbf{C}_{M}^{-1} \textbf{m}_{prior})\\ 这样就得到了最小二乘解。由上式可知,在线性反演中,在关键的步骤是确定矩阵G。
进一步,将上式改写为先验值+后续更新的形式:
令 \tilde{C}_M=(\textbf{G}^{t}\textbf{C}_{D}^{-1}\textbf{G}+\textbf{C}_{M}^{-1})^{-1}\\ 则 \tilde{\textbf{m}}=\tilde{C}_M(\textbf{G}^t\textbf{C}_{D}^{-1}\textbf{d}_{obs}+\textbf{C}_{M}^{-1} \textbf{m}_{prior})\\=\tilde{C}_M\textbf{G}^t\textbf{C}_{D}^{-1}\textbf{d}_{obs}+\tilde{C}_M\textbf{C}_{M}^{-1} \textbf{m}_{prior}\\=\tilde{C}_M\textbf{G}^t\textbf{C}_{D}^{-1}\textbf{d}_{obs}+\tilde{C}_M(\textbf{G}^{t}\textbf{C}_{D}^{-1}\textbf{G}+\textbf{C}_{M}^{-1} -\textbf{G}^{t}\textbf{C}_{D}^{-1}\textbf{G})\textbf{m}_{prior}\\ =\textbf{m}_{prior}+\tilde{C}_M\textbf{G}^t\textbf{C}_{D}^{-1}\textbf({d}_{obs}-\textbf{G}\textbf{m}_{prior})
注意上式推导中: \tilde{C}_M^{-1}=\textbf{G}^{t}\textbf{C}_{D}^{-1}\textbf{G}+\textbf{C}_{M}^{-1}\\ 上面推导告诉我们:当先验误差较大时, \textbf{C}_{D}^{-1} 较小,则每步更新就较小,反之就较大。
这说明:良好的先验信息在反演中非常关键。
2 案例分析:层析成像
走时层析成像是经典的线性反演问题,在地球科学与医学成像(CT)中都应用非常广泛。
在此过程中,最关键的步骤就算准确构建G矩阵。大尺度走时成像往往需结合射线追踪等来完成路径计算。
下面举一个简单的例子(细节见下文代码):
下面的总体思路:先假设一个模型,正演得到观测,再加噪声反演,看能否恢复模型。
下图方框中为待成像的区域,供划分为16个小方块,一共有22条射线穿过。
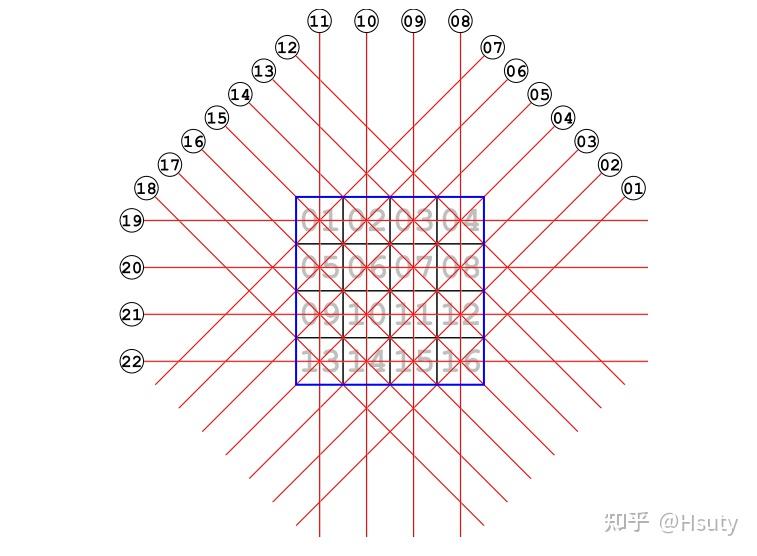
射线路径
若测量值d与区域介质性质m的关系为: d^i=\int_{R^i}^{}m(x,y)dl\\CT原理与此非常相似,将上式离散可得: d^i=\sum_{\alpha=1}^{16}{G_\alpha ^i} m^\alpha\\ 由于将待求区域划分成了16个小方格,因此 \alpha 取值为1到16,即每一次测量值d都与这16个小方格有某种关系。但实际上,由于每条测线经过的路径有限,其实每次测量只有部分小方格参与,这就意味着(1)每次测量只能对少数小方格有分辨率,因此需多方位多次测量;(2)G矩阵中零元素非常多,其为一个稀疏矩阵。
比如在本例子中,G矩阵为:
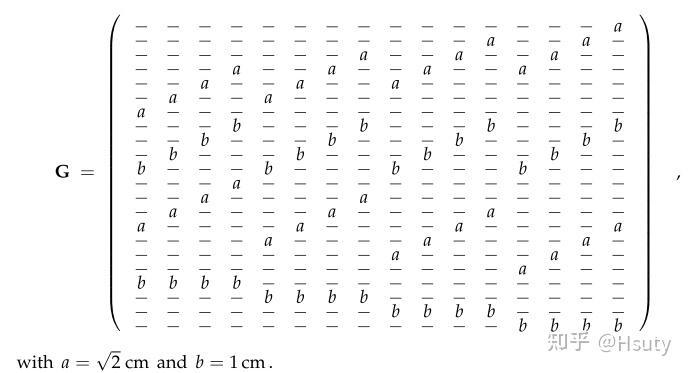
G矩阵
现在我们假设真实模型如下图:
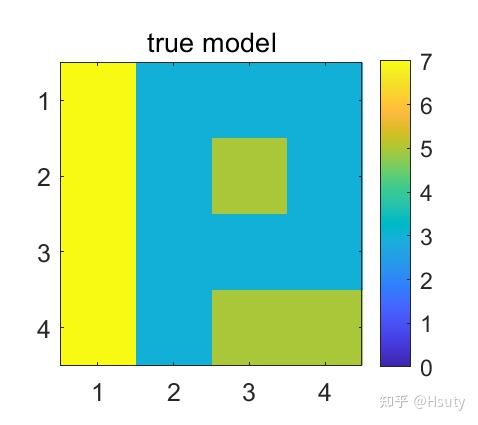
同时,假设先验值的标准差为1.5 cm^-1, 观测标准差为0.15 cm^-1,均符合高斯分布。
在一定范围内,生成9个先验模型:
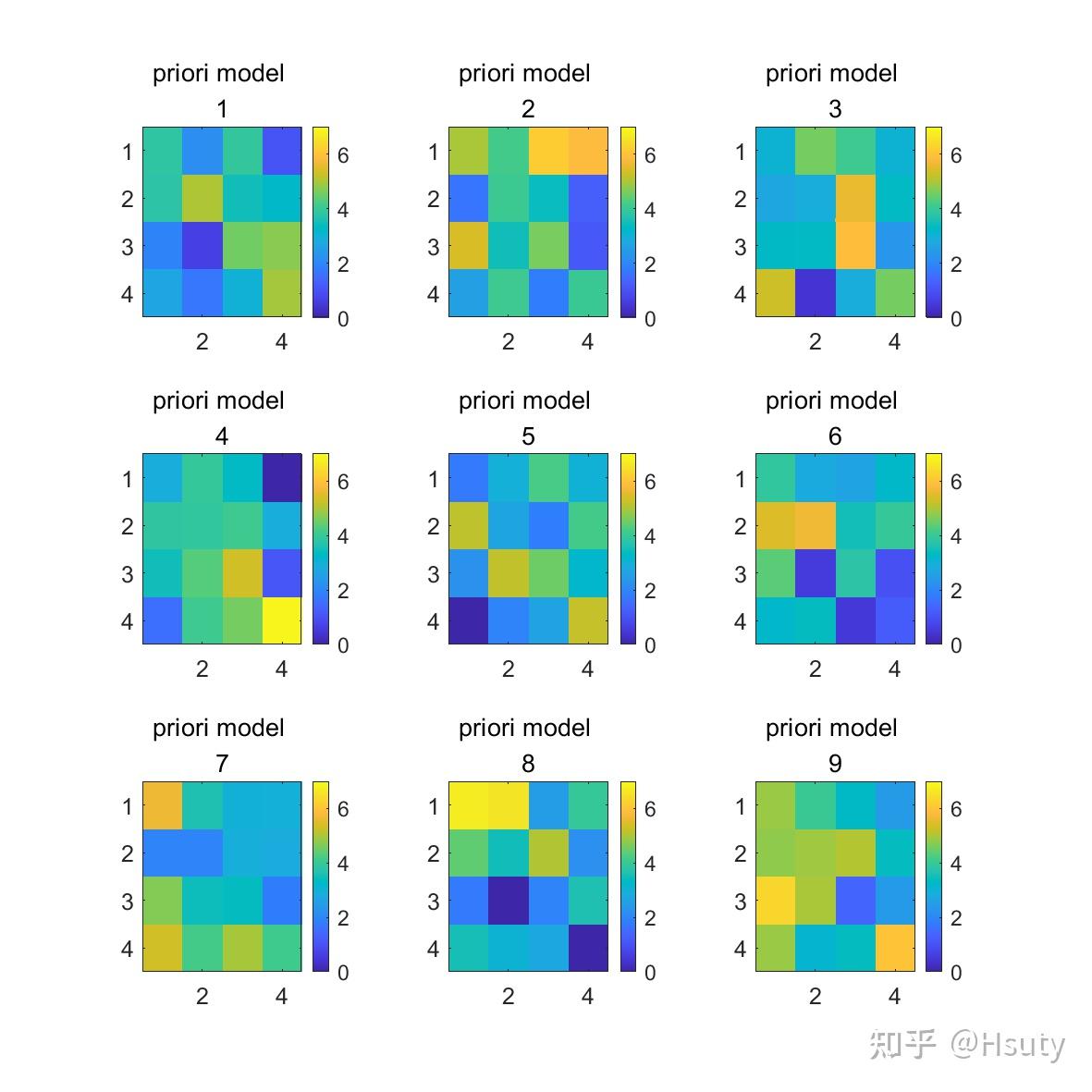
由上图可知,这些先验模型与真实值差距较大。
根据第一部分推导的线性反演公式,得到的反演结果如下:

我们可以发现P字中间那个黄色小方块,每个模型都恢复较好。这是因为大多情况下,测量的射线均通过于此方块,这就说明在层析成像中,射线的覆盖程度非常重要;覆盖好的地方,成像质量才高。
把上面得到的反演值做一个平均:
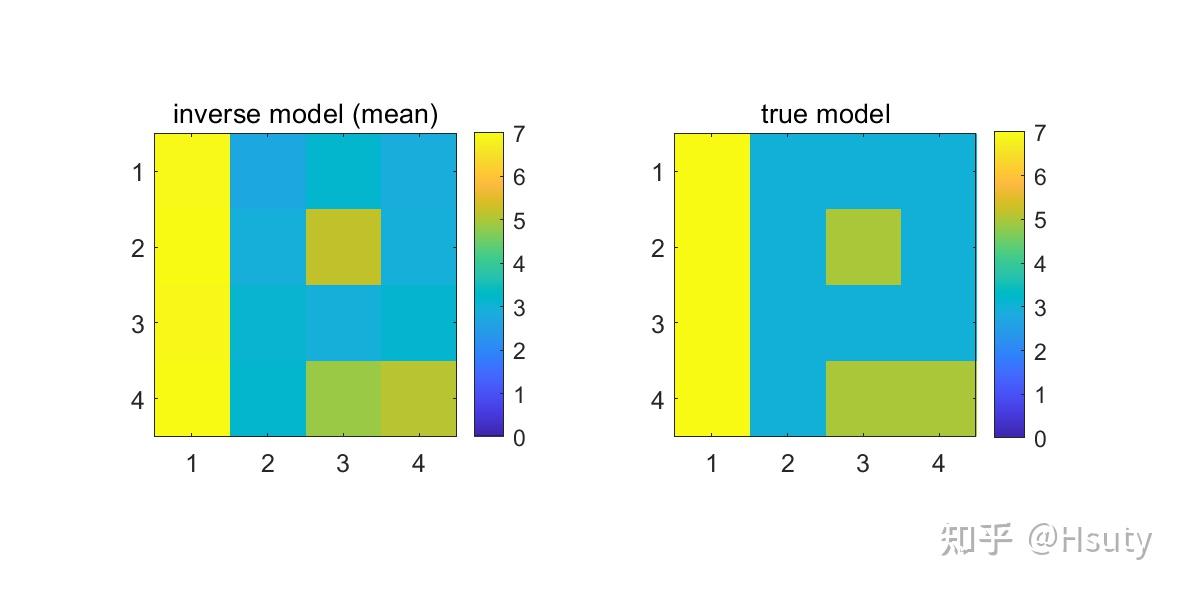
这就非常接近真实模型了,但也有差异,这说明由于噪声的存在与观测有限,我们不可能完全恢复模型。
最后,我们还可以分析一下,各方块之间的相关程度:
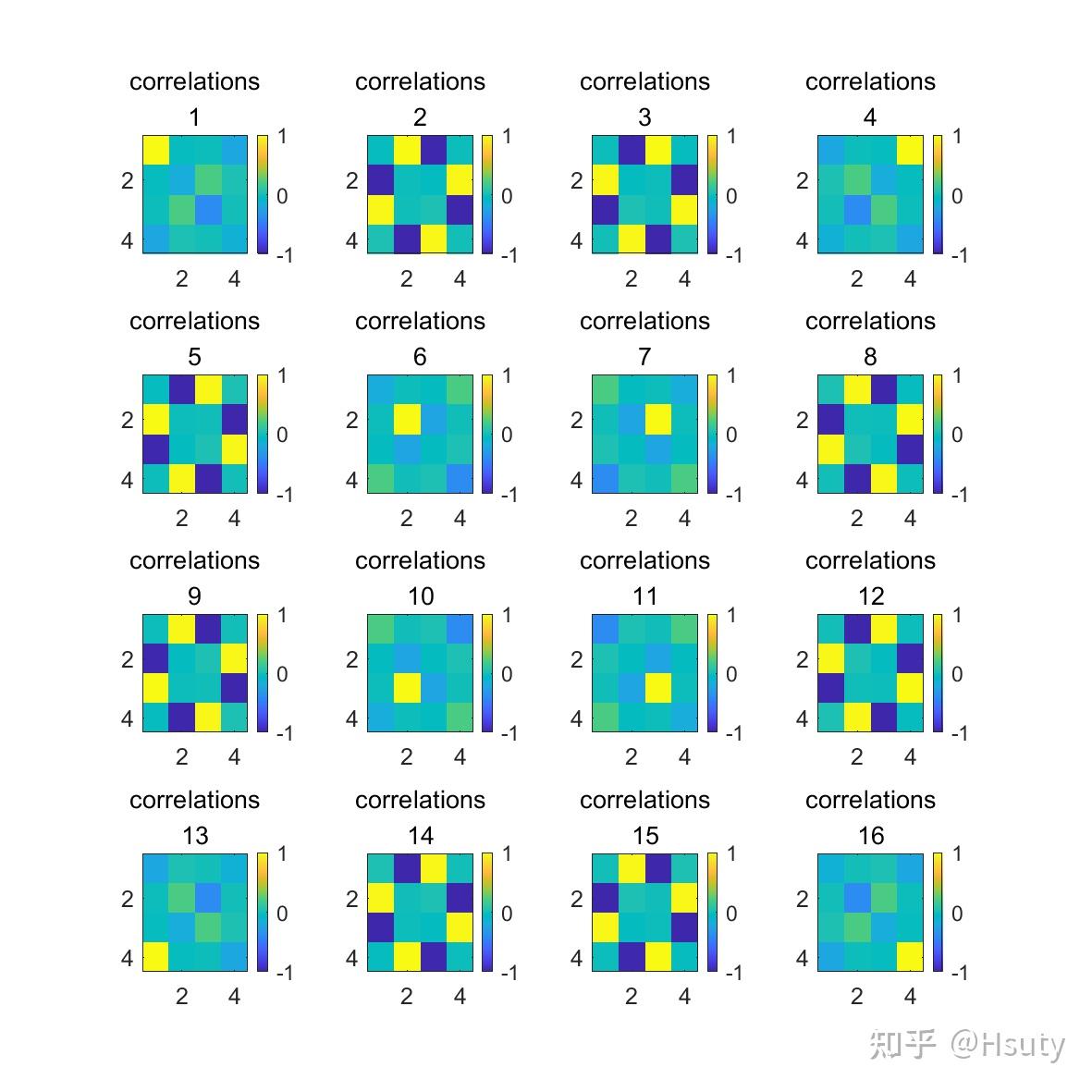
比如第一个小方块只与自身有关;而第2个小方块与第8、9、15正相关,3、5、14负相关,这说明这些小方块参数正确与否会影响到能否准确恢复第2个小方块的值。这也就是为什么第二个小方块的值较第一个小方块更难确定的原因之一。
3 相关代码
%ray tomography study, the linear least squares
%code by Hsuty, 2022-05-02
%the reference from http://www.ipgp.jussieu.fr/~tarantola/exercices/chapter_04/RayTomography.pdf
clc;clear;
%d = Gm, the linear problem,
%from data space + priori information to model space
% covariance matrix of data(observations) and priori information
G = zeros(22,16);d = zeros(22,1);m = zeros(16,1);
sqrt2 = sqrt(2);
% for matrix G, which depends on the geometry of the rays
G(1,16)=sqrt2;
G(2,12)=sqrt2;G(2,15)=sqrt2;
G(3,8) =sqrt2;G(3,11)=sqrt2;G(3,14)=sqrt2;
G(4,4) =sqrt2;G(4,7) =sqrt2;G(4,10)=sqrt2;G(4,13)=sqrt2;
G(5,3) =sqrt2;G(5,6) =sqrt2;G(5,9) =sqrt2;
G(6,2) =sqrt2;G(6,5) =sqrt2;
G(7,1) =sqrt2;
G(8,4) =1;G(8,8) =1;G(8,12) =1;G(8,16) =1;
G(9,3) =1;G(9,7) =1;G(9,11) =1;G(9,15) =1;
G(10,2)=1;G(10,6)=1;G(10,10)=1;G(10,14)=1;
G(11,1)=1;G(11,5)=1;G(11,9) =1;G(11,13)=1;
G(12,4)=sqrt2;
G(13,3)=sqrt2;G(13,8)=sqrt2;
G(14,2)=sqrt2;G(14,7)=sqrt2;G(14,12)=sqrt2;
G(15,1)=sqrt2;G(15,6)=sqrt2;G(15,11)=sqrt2;G(15,16)=sqrt2;
G(16,5)=sqrt2;G(16,10)=sqrt2;G(16,15)=sqrt2;
G(17,9)=sqrt2;G(17,14)=sqrt2;
G(18,13)=sqrt2;
G(19,1)=1;G(19,2)=1;G(19,3)=1;G(19,4)=1;
G(20,5)=1;G(20,6)=1;G(20,7)=1;G(20,8)=1;
G(21,9)=1;G(21,10)=1;G(21,11)=1;G(21,12)=1;
G(22,13)=1;G(22,14)=1;G(22,15)=1;G(22,16)=1;
% for priori information
m_priori_mean=3.5*ones(16,1); %priori value
s_m=1.5; %the standard deviation of a Gaussian distribution
C_prior=s_m^2*eye(16);% covariance matrix
L_priori = chol(C_prior)'; %cholesky decomposition
% priori distribution in the model space
m_priori_random = zeros(16,9);
width = 20;
height = 20;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
for ii = 1:1:9
x = -1 + 2*rand(1,16); %unifom random number in [-1,1]
m_random0 = sqrt(2)*erfinv(x); % Gaussian distribution of the random number
m_priori_random(:,ii) = m_priori_mean + L_priori*m_random0';
subplot(3,3,ii);
imagesc((reshape(m_priori_random(:,ii),[4,4]))');%reshape in matlab is column major order
title('priori model ',num2str(ii),'fontsize',12);
colorbar;caxis([0 7]);
set(gca,'fontsize',12)
end
saveas(gcf,'priori_model.png');
%%
%the true model set
m_true = [7,3,3,3,7,3,5,3,7,3,3,3,7,3,5,5]';
d_true = G*m_true;
sd=0.15; % the standard deviation of a Gaussian distribution for the observation
%add noise for the data_true to form the observations
x = -1 + 2*rand(1,22); %unifom random number in [-1,1]
d_random = sqrt(2)*erfinv(x);
dobs = d_true+sd*d_random'; %true obs + noise
C_obs = sd^2*eye(22); %covariance matrix of observations
m_post = zeros(size(m_priori_random));
%solve, for the linear problem, using the formula(3.37)
for ii = 1:1:9
m_priori = m_priori_random(:,ii);
m_post(:,ii) = inv(G'*inv(C_obs)*G+inv(C_prior))*(G'*inv(C_obs)*dobs+inv(C_prior)*m_priori);
end
width = 20;
height = 20;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
for ii = 1:1:9
m_res = reshape(m_post(:,ii),[4,4]);
subplot(3,3,ii);
imagesc(m_res');
title('posterior model ',num2str(ii),'fontsize',12);
colorbar;
set(gca,'fontsize',12);
caxis([0 7]);
end
saveas(gcf,'posterior_model.png');
%%
%the mean model of the posterior
m_post_mean = mean(m_post,2);
m_res = reshape(m_post_mean,[4,4]);
m_real = reshape(m_true,[4,4]);
width = 20;
height = 10;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
subplot(1,2,1)
imagesc(m_res');
axis equal;axis tight;
title('inverse model (mean)');colorbar;caxis([0 7]);
set(gca,'fontsize',12);
subplot(1,2,2);
imagesc(m_real');colorbar;caxis([0 7]);
axis equal;axis tight;
title('true model');
set(gca,'fontsize',12);
saveas(gcf,'posterior_model_mean.png');
%%
%check the resolution of the inversion results
C_post = inv(G'*inv(C_obs)*G+inv(C_prior));
%Although the matrix Cpost is, in principe symmetric,
% rounding errors may cause the Cholesky decomposition to work.
% For this reason, it is better to “resymmetrize” it.
C_post = 0.5*(C_post+C_post');
L_post = chol(C_post)';
%generate of random models of the posterior
%get the resolution of the data
width = 20;
height = 20;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
for ii = 1:1:9
x = -1 + 2*rand(1,16); %unifom random number in [-1,1]
m_random0 = sqrt(2)*erfinv(x); % Gaussian distribution random number
m_randomp = m_post_mean + L_post*m_random0';
m_randomp = reshape(m_randomp,[4,4]);
subplot(3,3,ii);
imagesc(m_randomp');%reshape in matlab is column major order
title('random models',num2str(ii));
colorbar;caxis([0 7]);
set(gca,'fontsize',12)
end
saveas(gcf,'posterior_random_models.png');
%%
% the standard deviation of the inverse results
dev = sqrt(diag(C_post));
devn = reshape(dev,[4,4]);
width = 10;
height = 10;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
imagesc(devn');
axis equal;axis tight;
title('the standard deviation');
colorbar;caxis([0 0.5]);
set(gca,'fontsize',12);
saveas(gcf,'posterior_standard_deviation.png');
%%
% the correlations of the off-diagonal elements of C_post
for ii = 1:1:16
for jj = 1:1:16
rou(ii,jj) = C_post(ii,jj)/(dev(ii)*dev(jj));
end
end
width = 20;
height = 20;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
for kk = 1:1:16
rou_res = reshape(rou(kk,:),[4,4]);
subplot(4,4,kk);
imagesc(rou_res');
title('correlations',num2str(kk),'fontsize',12);
colorbar;
set(gca,'fontsize',12);
caxis([-1 1]);
end
saveas(gcf,'correlations1.png');
%%
rou = C_post./(dev*dev');
width = 10;
height = 10;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
imagesc(rou);
axis equal;axis tight;
title('the correlations of C_{post}');
colorbar;set(gca,'ydir','normal');
caxis([-1 1]);set(gca,'fontsize',12);
saveas(gcf,'correlations2.png');
%%
%resilution operator
R = C_prior*G'*inv(G*C_prior*G'+C_obs)*G;
figure('Units','Centimeters','Position',[1 1 width height],'color','w');
imagesc(rou);
axis equal;axis tight;
title('resolution operator R');
colorbar;set(gca,'ydir','normal');
caxis([-1 1]);set(gca,'fontsize',12);
原文地址:https://zhuanlan.zhihu.com/p/654028187 |
 /3
/3 