t分布介绍
t分布最早是由英国统计学家Gosset W S在1908年以笔名“student”发表论文,证明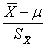 服从自由度ν=n-1的t分布,故t分布也称为Student t分布(Student’s t-distribution),t分布主要用于总体均数的区间估计和t检验等。
服从自由度ν=n-1的t分布,故t分布也称为Student t分布(Student’s t-distribution),t分布主要用于总体均数的区间估计和t检验等。
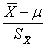 中
中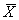 是样本的均数。
是样本的均数。 是总体的均数,
是总体的均数,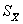 是均数的标准误。关于总体参数和样本参数的区别我已经在第一篇中详细阐述了,这里不再赘述。怎么来理解呢?比如我们抽了100个样本,每个样本的样本含量为20。因此我们可以得到100个样本均数和标准差。我们可以将这100个样本均数当做新的变量值,再求均数,就得到
是均数的标准误。关于总体参数和样本参数的区别我已经在第一篇中详细阐述了,这里不再赘述。怎么来理解呢?比如我们抽了100个样本,每个样本的样本含量为20。因此我们可以得到100个样本均数和标准差。我们可以将这100个样本均数当做新的变量值,再求均数,就得到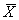 。样本均数的标准差也称为均数的标准误,表示为
。样本均数的标准差也称为均数的标准误,表示为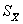 ,通常用标准误来反应抽样误差。其中
,通常用标准误来反应抽样误差。其中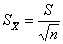 ,我们可以看到,当样本含量n越大,均数标准误越小,抽样误差越小,表示用样本均数来估计总体均数时的可靠性越大。
,我们可以看到,当样本含量n越大,均数标准误越小,抽样误差越小,表示用样本均数来估计总体均数时的可靠性越大。
在本系列第二篇中(浅谈IVD统计系列--资料类型及正态分布),我介绍了标准正态分布(Z分布),Z分布是正态分布通过标准正态分布转化而来。其实t分布在Z分布的基础上,再一次进行了转换。可以将t分布简单理解为,以样本均数替代了Z分布中的X,以标准误替代了σ。即t=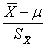 。其分布曲线如下图所示。可以看到t分布只有一个参数,即自由度,并且t分布不是一条曲线,而是一簇曲线,当自由度不同时,曲线的形状不同。当自由度为∞时,t分布就是标准正态分布(Z分布),标准正态分布是t分布的特例。
。其分布曲线如下图所示。可以看到t分布只有一个参数,即自由度,并且t分布不是一条曲线,而是一簇曲线,当自由度不同时,曲线的形状不同。当自由度为∞时,t分布就是标准正态分布(Z分布),标准正态分布是t分布的特例。
t分布的应用
总体均数可信区间的计算
根据总体标准差σ是否已知和样本含量n的大小,总体均数可信区间的估计方法通常有t分布和z分布两种。
统计应用的本质是统计量的换算,我们最常用的就是将t值或者其他统计量换算成P值,做显著性检验,或者将P值换算成t值或者其他统计量,来计算均数的置信区间。为了方便应用,统计学家编制了不同自由度下t值与相应概率关系的t界值表。因此,当我们知道了样本量,置信水平,就知道了对应的t值。t界值表中,横标目为自由度ν,纵标目为尾部概率P或α。一侧尾部面积称为单尾概率,其对应的t界值用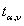 表示;双侧尾部面积之和称为双尾概率,其对应的t界值用
表示;双侧尾部面积之和称为双尾概率,其对应的t界值用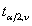 表示。由于t分布以0为中心左右对称,故t界值表中只列出了正值,若计算的t值为负值则用其绝对值查表。
表示。由于t分布以0为中心左右对称,故t界值表中只列出了正值,若计算的t值为负值则用其绝对值查表。
同一自由度的双侧概率P为单侧概率P的两倍。那么在什么情况下选择用双侧,什么情况下选择用单侧呢?选择单、双侧界值应依据专业知识确定。例如,体质指数(BMI)无论过高或过低均属异常,参考值范围应是双侧;而有些指标只有在过大或者过小时为异常,如肺活量过低为异常,因此只需确定下限,因此参考值范围应是单侧。
对于t分布,t=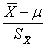 ,通过这个公式的换算,知道样本均值,标准差,样本含量就可以算出总体均数的可信区间。
,通过这个公式的换算,知道样本均值,标准差,样本含量就可以算出总体均数的可信区间。
1) σ未知:按t分布。P=1-α,因此总体均数的双侧(1-α)可信区间为
2) σ已知或者σ未知但n足够大(n>50),按z分布计算置信区间。上面我们已经提到过,当自由度趋近于无穷时,t分布就是标准正态分布,一般认为t分布在样本量较小时更具有统计优势,t分布的发现使得小样本统计推断成为可能。Z分布在样本量较大时具有优势,但是这个界限没有一个统一的说法,有的认为以n=60为界,有的认为以n=40为界,还有的以n=100为界的。
t检验
关于假设检验的目的,我在浅谈统计系列之基本概念中已经详细阐述过,一句话总结,就是比较两个样本之间有无显著性差异。那t检验的实质就是将样本统计量换算成t值,再将t值换算成最直观明了的P值,从而判断两个样本之间有无显著性差异。
1)假设检验的基本步骤
A. 建立检验假设,确定检验水准。假设有两种:一种是原假设、无效假设或者零假设,记为H0,假设样本所代表的总体参数(如未知总体均数 )与已知总体参数(如总体均数
)与已知总体参数(如总体均数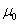 )相等,H0:
)相等,H0: =
=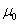 ;另一种是备择假设,也称对立假设,记为H1,是与H0相联系、对立的假设,H1:
;另一种是备择假设,也称对立假设,记为H1,是与H0相联系、对立的假设,H1:
 。H1假设直接体现了所进行的假设检验是双侧检验还是单侧检验。若H1是
。H1假设直接体现了所进行的假设检验是双侧检验还是单侧检验。若H1是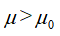 ,或
,或 ,则此检验为单侧检验,其不仅考虑是否有差别,还考虑差别的方向。若H1为
,则此检验为单侧检验,其不仅考虑是否有差别,还考虑差别的方向。若H1为 ,则此检验为双侧检验。
,则此检验为双侧检验。
检验水准也称为显著性水准,是预先规定的判断小概率事件的概率尺度,记为α。在实际工作中,α通常取0.05或0.01,即若某个事件发生的概率小于0.05或0.01,认为其是小概率事件。
B. 计算检验统计量
根据研究目的、设计方案、变量或资料类型及其分布特征、假设检验方法适用条件等选择检验统计量。比如通常我们用的比较多的有t检验,F检验,卡方检验等,那么计算的检验统计量分别为t值,F值, 值。
值。
C. 确定P值,作出推断结论
求出检验统计量后,查附表中相应的统计界值表即可得出概率P值,从而作出统计推断。若P>α,按α检验水准不拒绝H0,认为差异无统计学意义,即无显著性差异;若P≤α,拒绝H0,接受H1,两个样本间有显著性差异。
2)t检验的应用条件和类型
首先,需要明确的是t检验所适用的资料类型是计量资料。其次,应用t检验时,各样本均来自于其总体的随机样本;再者,各样本均来自于正态分布总体,如果不确定,需要做正态性检验;最后两独立样本均数比较时,要求两总体方差相等。
A. 单样本定量资料的t检验
指的是样本均数与总体均数比较的t检验,又称单样本资料的t检验,实际上是推断该样本来自的总体均数 与已知的某一总体均数
与已知的某一总体均数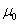 有无差别。
有无差别。
具体应用也是根据根据假设检验的三大步骤进行。
第一步:建立检验假设,确定检验水准。
第二步:计算检验统计量。t=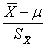 。将样本均数
。将样本均数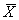 ,和总体均数
,和总体均数 ,标准误
,标准误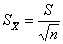 代入上式,算出检验统计量t值。
代入上式,算出检验统计量t值。
第三步:根据自由度 ,检验水准α(0.01或0.05)来查t界值,用算出的t值和t界值进行比较,若t值大于t界值,则P小于检验水准,拒绝原假设,两样本差异显著。反之,无显著性差异。
,检验水准α(0.01或0.05)来查t界值,用算出的t值和t界值进行比较,若t值大于t界值,则P小于检验水准,拒绝原假设,两样本差异显著。反之,无显著性差异。
B. 配对设计定量资料的t检验
所谓的“配对”实际上就是“一对一”。通常有两种类型,“异体配对”和“自身配对”。“异体配对”是指将某些重要特征相似的每两个受试对象配成一对,将每对受试对象进行随机分配后,分别给予两种不同的处理。“自身配对”是指同一受试对象分别接受两种处理。比如为了测试某减肥药的效果,让15位身体偏胖的人服用该药,通过测量服药前和服药后的体重,检验该药有无效果。
同样的,按照假设检验的三大步骤进行。不过,配对检验的检验假设与上述有所不同。配对设计资料的分析着眼于每一对中两个观察值之差,这些差值构成一组资料,用t检验推断差值的总体均数是否为“0”,检验假设为H0: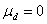
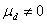
:,即差值的总体均数不等于“0”,当H0成立时,检验统计量
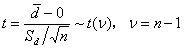 ,其中
,其中 为差值的均数,
为差值的均数, 为差值的标准差,n为对子数。
为差值的标准差,n为对子数。除了上述两种t检验外,还有两独立样本均数比较的t检验。这部分比较复杂,会在下一篇中连同SPSS软件实现详细说明。
其实统计学习并非理解上的难度,个人认为统计是需要系统的去学习的,每种资料类型,在不同实验条件下所用到的统计学方法也会不同,现在有非常多的统计软件供我们选择,但是统计软件不会告诉你用那种统计方法进行分析,还是需要自己了解数据特征后,并且熟练正确的掌握每种统计方法的应用条件,才能准确有效的分析自己的数据,本系列文章肯定不会面面俱到,只希望能为大家提供学习的思路。





 /3
/3 





 浙公网安备33010802005999号
浙公网安备33010802005999号


